【数学】積分漸化式

対象：理系(数学III)

今回は　積分漸化式　を確認しましょう

積分漸化式は　部分積分　を利用して作ります
今回の結果はすぐに使えるようにしておきましょう

wallis　の公式

ちなみに　最後の項(最も左の項)について
$${n \ が偶数のとき　→　I_0=\dfrac{\pi}{2}}$$
$${n \ が奇数のとき　→　I_1=1}$$
となっていて，それぞれ次の面積の半分　を表しています

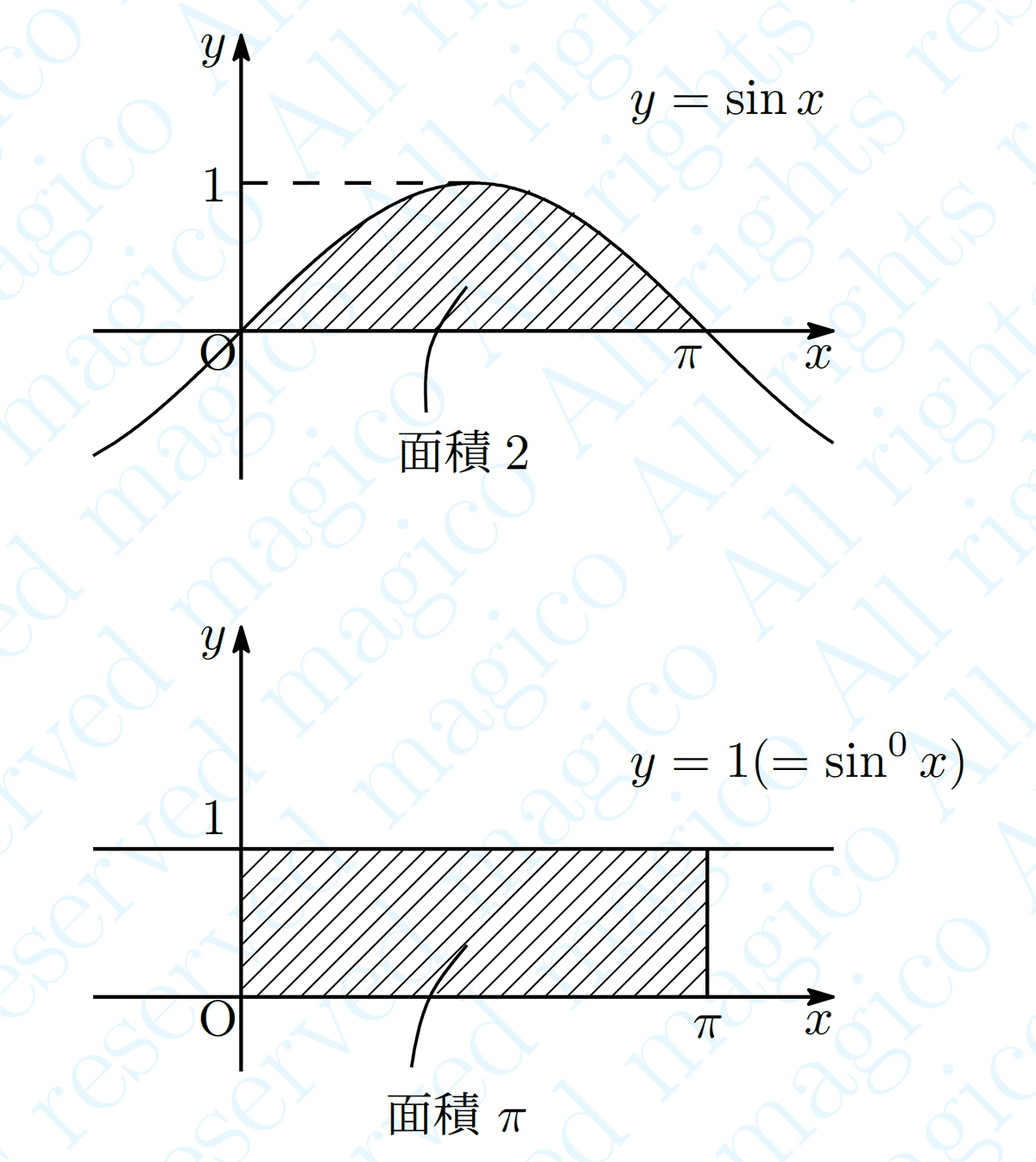
難関大学では　積分計算の際に　誘導無しでこれを用いることがあります
次のように　すぐに使えることが求められます

$${\displaystyle \int_{0}^{\frac{\pi}{2}}\cos^n x \ dx}$$　については
平行移動して考えれば　$${\sin^n x}$$　の場合とまったく同様であることを視覚的に確認してください

その他　$${\tan^n x}$$　などもありますので　参考書等で確認しましょう

もう1問　対数　です

今回も　部分積分　ですが
対数関数の部分積分なので　隠れた($${x'}$$)を補って考えましょう