【数学】多変数関数

対象：定期試験以上

2次関数を題材として，多変数関数の最大最小を考えます

多変数関数は，変数が2つ以上ある関数であり
例えば　2変数関数　x+y　や　x^2+y^2　などは
それらの値を$${z}$$とおくと
$$z=x+y，\ z=x^2+y^2$$　となり
空間内での曲面を表します

しかし　最大最小を考える際には　空間内の曲面を考える必要はありません

ここでは　2変数関数　を題材として学びます

2変数　といってもその関係上　2種類に分けられます
1つは従属変数　もう1つは独立変数です

カンタンに言えば
一方が決まれば他方も決まるしばられた関係・・・従属変数
お互い自由に動ける・・・独立変数
ということです

まずは，独立2変数の問題からやりましょう

$${x}$$と$${y}$$の間には，特に何の関係もないので
お互いが自由に動ける　独立変数　です

解き方は　「まず一方を定数扱い(固定)して」　ということで
$${y}$$を定数として　$${x}$$の2次関数として扱いました
その後，得られた最小値を$${y}$$の関数として考え
最小値の最小値　を求めればよいです

個人的にあまり好きな単語ではないですが「予選決勝法」などと呼ばれることがあります

次は　従属変数　の場合です

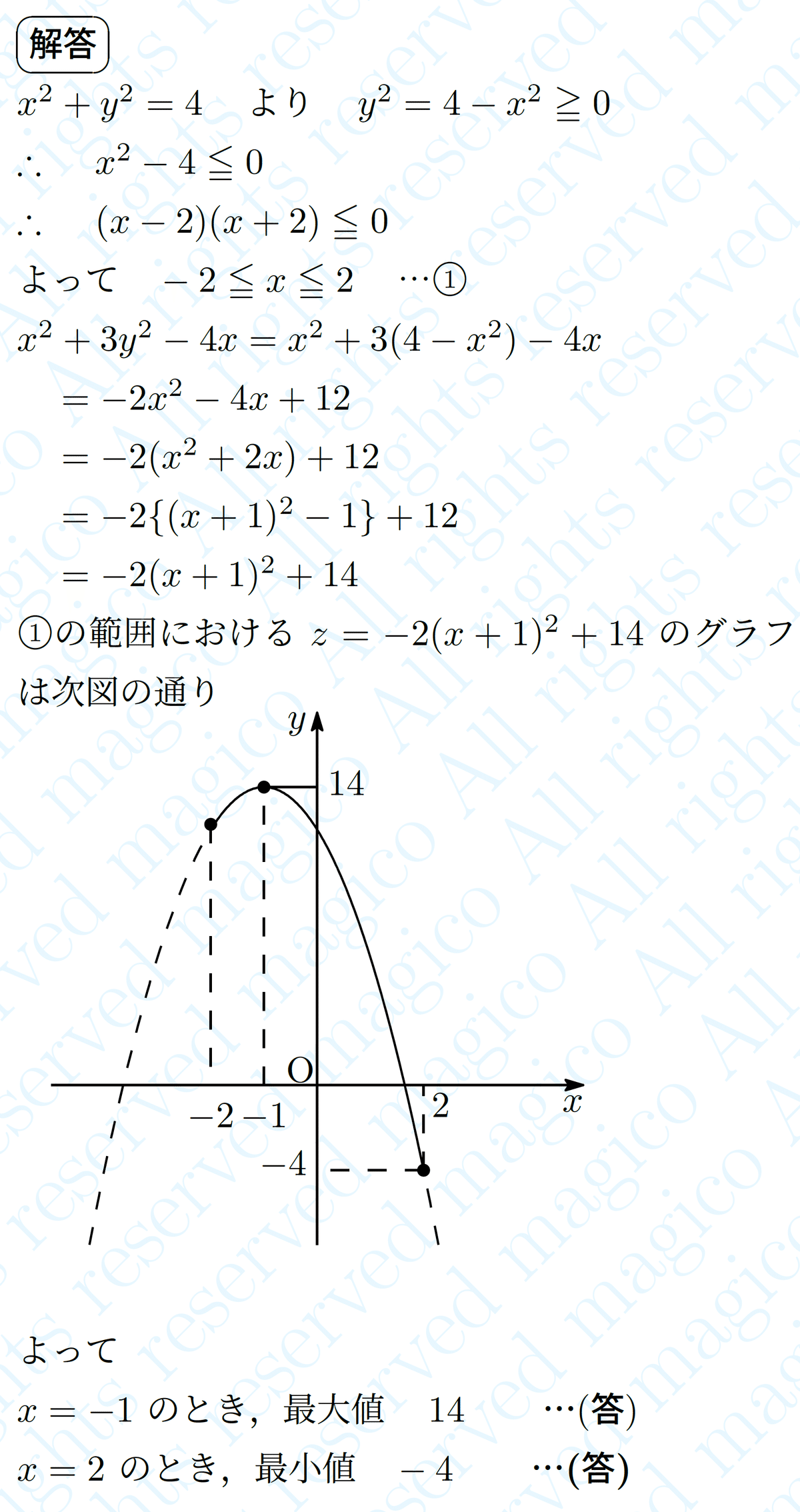
$${x}$$と$${y}$$に一定の関係があるので従属関係です
したがって，原則に従い　まずは1文字を消去しましょう

ただし，今回の場合には$${x}$$や$${y}$$の変域には制限があります
(数学IIで円を学習すればさらに理解できる)
したがって　$${y}$$を消去したあと　限られた定義域で最大最小を考えることになります

独立2変数，従属2変数の問題を1問ずつやりました
それぞれの解き方の違いは

でした

従属2変数の問題のほうが　1文字だけになってカンタンだ
と感じる人もいると思いますが
実は　従属2変数では　ちょっと問題が変わればまた別の議論が必要となります(文字が消去できない．．．)
独立2変数のほうが実はカンタンなんですね

2次関数だけでなく　他の分野でも使う基礎論となりますから
しっかり習得しましょう