
【数学】サイクロイド・アステロイド
対象:理系(数学III) 定期試験以上
今回は サイクロイドとアステロイド について学習しましょう
いずれも 転がる円上の1点の軌跡 です
ここでの目的は それらを媒介変数表示すること とします




転がった円弧=転がった地面 を利用します
ベクトルを利用すると表現がラクですね
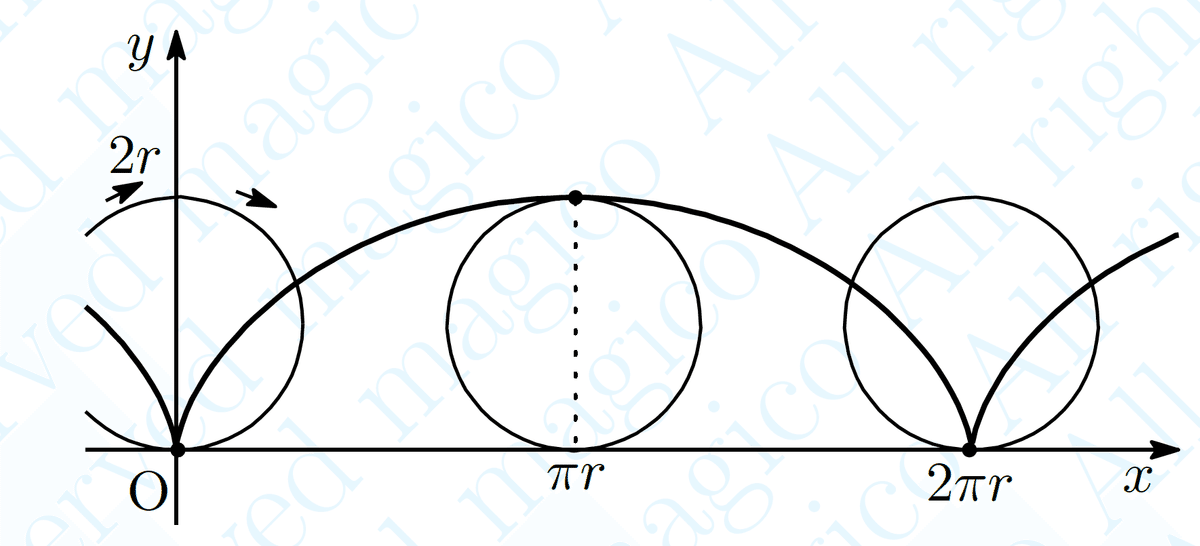

結果は覚えていなくても構いません
次はアステロイドです




サイクロイドと同じように
転がった円弧 = 転がった地面 として
ベクトルを利用して考えます
サイクロイドの場合もそうでしたが 角度を考える際に
$${x}$$軸と平行な線を書くこともポイントです
アステロイドの式は覚えやすいので 覚えておくとよいでしょう
(必須ではない)


アステロイドは 円の内側を転がる円 ということで
内サイクロイド(ハイポサイクロイド) の一種です
逆に 円の外側を転がる円 という 外サイクロイド(エピサイクロイド)もあります
半径比が 4:1 のときの内サイクロイドをアステロイドといいます

また アステロイドは 線分の通過領域 としての性質をもちます

代表的な2つの曲線を扱いましたが
転がる円で 円の内部の点の軌跡 であったりすることもあります
上記の方法をぜひ身につけてください
