
スケジューリング問題を解く③-1
ゴール設定は以下の問題を解くことです。
・工場で作らねばならない2種類の製品を間に合わせる。
・納期 A:明日 B:明々後日(指定日の夜に出来てればいい)
・着手可能日 A:今日 B:今日 (材料が来るのが遅い時がある)
・必要工数 A:1人日 B:2人日(人日=◯人が✕日かかるの意)
・作業者は1人しかいない。
・いつ、どの順番で着手すれば間に合うか?
まずは、最大流問題という計算方法を②で挙げた資料で調べてください。
(ネットでも分かりやすい解説がすぐにみつかります)
後で実際の問題に合わせるとして、今は適当なグラフを描きます。
👉は太さを持つパイプ(アーク:矢印)、
アルファベットはパイプを繋ぐジョイント(ノード:点)です。
👉の横に書かれている数字はパイプの太さです。
パイプの太さによって、流れる量が変化します。
======================
Start 👉1👉 A 👉2👉 B 👉5👉 Goal
👇3 👆1 👆2
C 👉2👉 D 👉2👉 E
======================
上の図で、StartからGoalまで水を流します。
水圧を上げると全てのパイプが水で埋まりますが、
今はGoalから流れ出す水が一定値になったら、
それ以上は水量を増やさないとします。
Q:Goalから流れ出す最大流は幾つですか?
頭で考えると… 4ですかね…
この手の問題は人が考えなくて良いのです。
Mathematicaで計算しましょう。
(Excelのソルバー、Python、Julia、PrologでもOKです)
高校の物理で電気の時間に習った、
キルヒホッフの法則を各点(ノード)毎に数式にしてください。
各点に入ってくる量=各点から出ていく量
変数は矢印(アーク)の部分。
1行目でgoalを最大化したいと宣言。
2〜4行目で矢印(アーク)の範囲を指定。
5〜7行目で各点におけるキルヒホッフの法則。
8行目で使う変数を並べる。
9行目で「整数で計算せよ」と書きます。
Program1:自力でネットワークを書く
Maximize[{goal,
0 <= startToA <= 1 && 0 <= aToB <= 2 && 0 <= bToGoal <= 5 &&
0 <= startToC <= 3 && 0 <= cToD <= 2 && 0 <= dToA <= 2 &&
0 <= dToE <= 2 && 0 <= eToB <= 2 &&
start == startToA + startToC && startToA == aToB - dToA &&
aToB == bToGoal - eToB && startToC == cToD && cToD == dToA + dToE &&
dToE == eToB && bToGoal == goal, start == goal},
{startToA, aToB,bToGoal, startToC, cToD, dToA, dToE, eToB, start, goal},
Integers]{3, {startToA -> 1, aToB -> 2, bToGoal -> 3, startToC -> 2, cToD -> 2,
dToA -> 1, dToE -> 1, eToB -> 1, start -> 3, goal -> 3}}暗算でミスりました。だから人が計算しては駄目なのです。
答えは3
ですね。
ただ、この書き方だと点(ノード)の数が増えると大変ですよね。
実はこの計算、PythonのNetworkXを使うともっと簡単です。また後で。
(色々と制約があるので、全ての問題をNetworkXでは書けません。
そこでラスボスは列生成法で片付けます。)
このように、現実の問題をグラフに置き換える抽象的なスキルが必要になってきます。教科書を読むと非常に難しい定式化をしていますので、それを書いたり読めるようになるのが理想ですが、私はこの方法でも充分だと思っています。
いい機会なのでMathematicaで上図のグラフを書いてみましょう。
最大流問題や最小コスト最大流問題ならばMathematicaで関数が用意されているので、こっちの方が楽かもしれません。
Program2:Mathematicaの機能でグラフを作る
gra = Graph[{"S" \[DirectedEdge] 1, 1 \[DirectedEdge] 2,
2 \[DirectedEdge] "G", "S" \[DirectedEdge] 3, 3 \[DirectedEdge] 4,
4 \[DirectedEdge] 1, 4 \[DirectedEdge] 5, 5 \[DirectedEdge] 2},
EdgeCost -> {1, 1, 1, 1, 1, 1, 1, 1},
EdgeCapacity -> {1, 2, 5, 3, 2, 1, 2, 2},
EdgeLabels -> {"S" \[DirectedEdge] 1 -> 1, 1 \[DirectedEdge] 2 -> 2,
2 \[DirectedEdge] "G" -> 5, "S" \[DirectedEdge] 3 -> 3,
3 \[DirectedEdge] 4 -> 2, 4 \[DirectedEdge] 1 -> 1,
4 \[DirectedEdge] 5 -> 2, 5 \[DirectedEdge] 2 -> 2},
VertexLabels -> Placed[Automatic, Center], VertexSize -> .25]1-3行目がグラフの構造
4行目が線(エッジ)の費用、コスト 通過すると費用が掛かります。
5行目が線(エッジ)の容量
6-9行目が線(エッジ)に付けるラベル ここでは費用の数字をつけます。
10行目が点(ノード)に付けるラベル ここでは丸数字にします。
これを実行するとグラフが描画されます。
Mathematicaでコードを書けば記号は変換されるので、文法を記憶する必要はありません。ドキュメントが充実しているのでコピペでOKです。

これで最大流問題を解きます。
FindMaximumFlow[gra, "S", "G"]
3あっさりと答えが出ます。簡単な問題の場合にはこちらの方法が楽です。
お次は最小コスト最大流問題。
最大流を求めつつ、線(エッジ)の重みをなるべく少なくしたいというものです。
今はEdgeCostを全て1にしてましたが、ここの値を変える事で通りたくない道や組合せはコストを高くする事で通りにくくなります。
(例えばメインの機械はコストを低く、保険機は高くなど)
FindMinimumCostFlow[gra, "S", "G"]
13あれ。この方法ではコードは書きやすいですが、
分岐してるとどこにどの流れなのか分かりにくい欠点があります。
どこのエッジにどれだけの流れがあるのか、数字では見られないようです。
これは困りますね。(実際にはこの関数、使いませんが…)
ビジュアルには確認できます。
[ScriptCapitalF] =
FindMinimumCostFlow[gra, "S", "G", "OptimumFlowData"];
\[ScriptCapitalF]["CostValue"];
\[ScriptCapitalF]["FlowGraph"]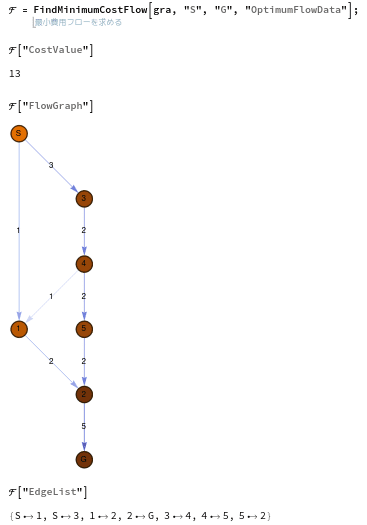
PythonのNetworkXでも同様の事が出来ますが…
今回はMathematicaで書きます。その理由は
に書きました。
次はいよいよ 時系列ネットワーク問題です。
そこでようやく、ゴール目標である問題をグラフで表現できます。
最後に(可能ならば)列生成法で終わりましょう。
