グラフ理論について（１）

みなさん、こんにちは。

今回はグラフ理論とは何かについて例を用いて中学生や高校生にもわかりやすく紹介していきたいと思います。

基礎レベルから応用レベルまで紹介できたらなと思っています。

【１】グラフ理論とは何か

グラフという言葉は聞きなれた人も多いとは思います。統計を用いるときの円グラフや棒グラフ、中学校の数学の授業で出てきた比例のグラフなどを想像した人も多いのではないでしょうか。

しかし、グラフ理論における「グラフ」というのはそれらとは全く異なるものなのです。

では、グラフ理論におけるグラフとはどのようなものなのでしょうか。

グラフとは、点(vertex)と辺(edge)で表された「図形」のことである。

では、グラフ理論における基礎知識について紹介していきます。

【２】グラフの基礎知識

一般的にグラフは、いくつかの点とそれらを結ぶ線分からなる図形のことを指します。

このときに重要であることは、どの2点を結んでいるかです。

それらが交差していたり、曲線であったりしても問題にはしません。

上のグラフは形は全く違いますが、どれも同じグラフです。

グラフ理論について勉強するために必要な知識や用語について記述していきます。

• グラフの頂点と交わっている辺の本数を「次数」という。

• 始点と終点が同じものを「閉路」という。

• どの頂点からどの頂点へもつながっているグラフを「連結」という。

• 二点を結ぶ２本以上の線のことを「多重辺」という。

• 辺の端点が１点からなる辺のことを「ループ」という。

• 広義グラフ・・・多重辺とループが許されているグラフ。

• 多重グラフ・・・多重辺は許されているが、ループは許されていないグラフ。

• 単純グラフ・・・多重辺もループも許されていないグラフ。

【３】重要なグラフ

①連結グラフと非連結グラフ

連結グラフは、グラフの中のどのような2点を選んでもたどることができるようなグラフのことをいいます。厳密にいうと、任意の2点の間に道が存在するようなグラフのことを表します。

非連結グラフは、連結グラフではないようなグラフのことを表します。

左のグラフが連結グラフで右のグラフが非連結グラフです。

連結グラフはどの２点を選んでもたどることができることが分かりますね。

非連結グラフは四角形のグラフと三角形のグラフがつながっていないため、たどることができない２点が存在してしまいます。

②完全グラフ

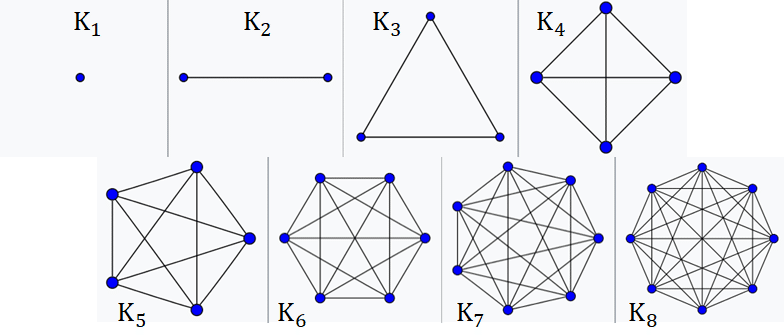
相異なる二つの頂点がすべて隣接しているグラフを「完全グラフ」といいます。

ｎ個の頂点からなる完全グラフを Kn と表します。

③2部グラフ

グラフの点を赤と青の2つの色に塗り分けた際に 赤い頂点同士の点、青い頂点同士の点それぞれに辺がないようなグラフのことを2部グラフといいます。

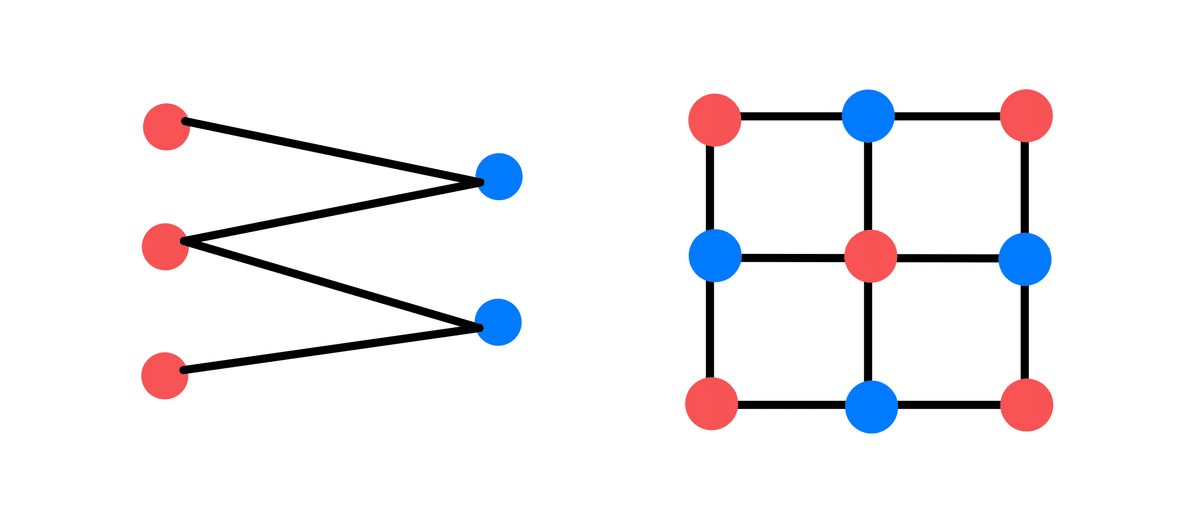
2部グラフの中でも、赤いすべての頂点と青いすべての頂点を結ぶような辺が全部あるようなグラフのことを完全2部グラフといいます。

赤い頂点の数が m、青い頂点の数が n のときの完全2部グラフを記号で Km,n と表します。

④正則グラフ

グラフのすべての点における次数が同じようなグラフのことを正則グラフといいます。それぞれの次数がすべて n であるとき、n 次正則グラフ (n-正則グラフ)と呼びます。

ちなみに完全グラフは必ず正則グラフになります。

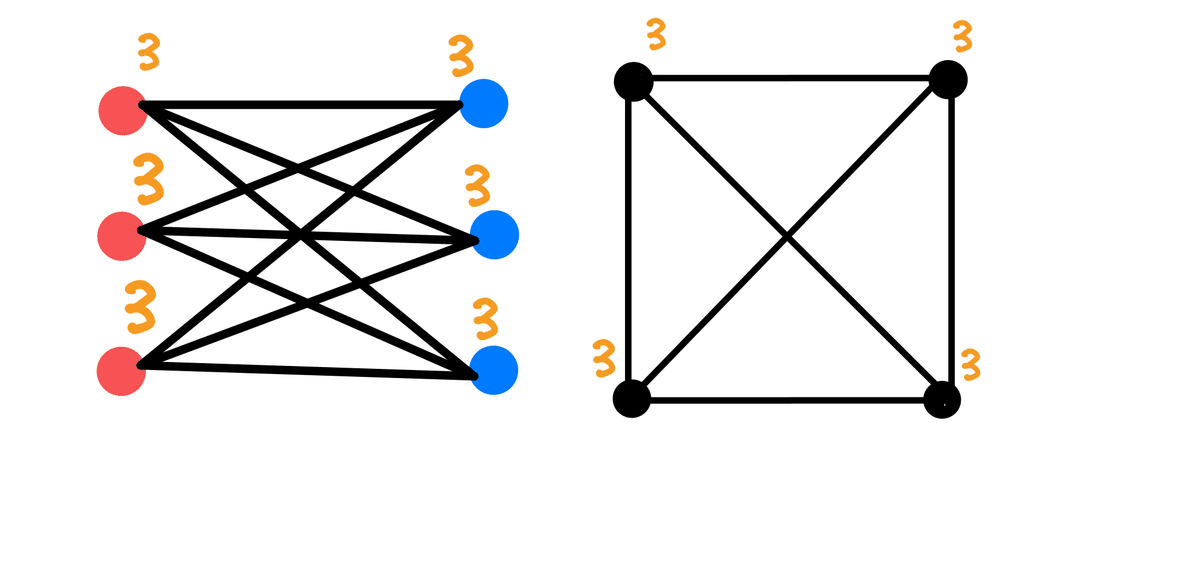
例えば、上の右のグラフを見ると、K₄は3次正則行列にもなることが分かります。

⑤補グラフ

あるグラフにおいて、もともと辺があった場所の辺をなくし、もともと辺がなかった場所の辺をつけた（辺の有無を反対にしたような）グラフのことを補グラフといいます。

【４】最後に

今回はグラフ理論の基本的な知識について紹介しました。

次回は、グラフの一筆書きについて紹介していきたいと思います。

最後まで読んでいただき、ありがとうございました。