HADを使ってみた：6.散布図

2021年1月22日 14:46

散布図を描いてみる

さて，だんだん分析っぽさが増してきました。今回は散布図です。手順は，

散布図を描きたい変数を２つ以上指定⇒【分析】⇒散布図にチェック

「散布図」のすぐ下に「グループ別」のオプションがありますが，これはのちほど。散布図は，２つの連続変数どうしの関係をプロットしますから，当然２つの変数を設定する必要があるのですが，３つ以上設定したらどうなるのでしょうか？　こちらからやってみましょう。iris のデータの，がく長，がく幅，花弁長，花弁幅を４つとも使用変数に設定して分析すると，こんな感じで出力されます。

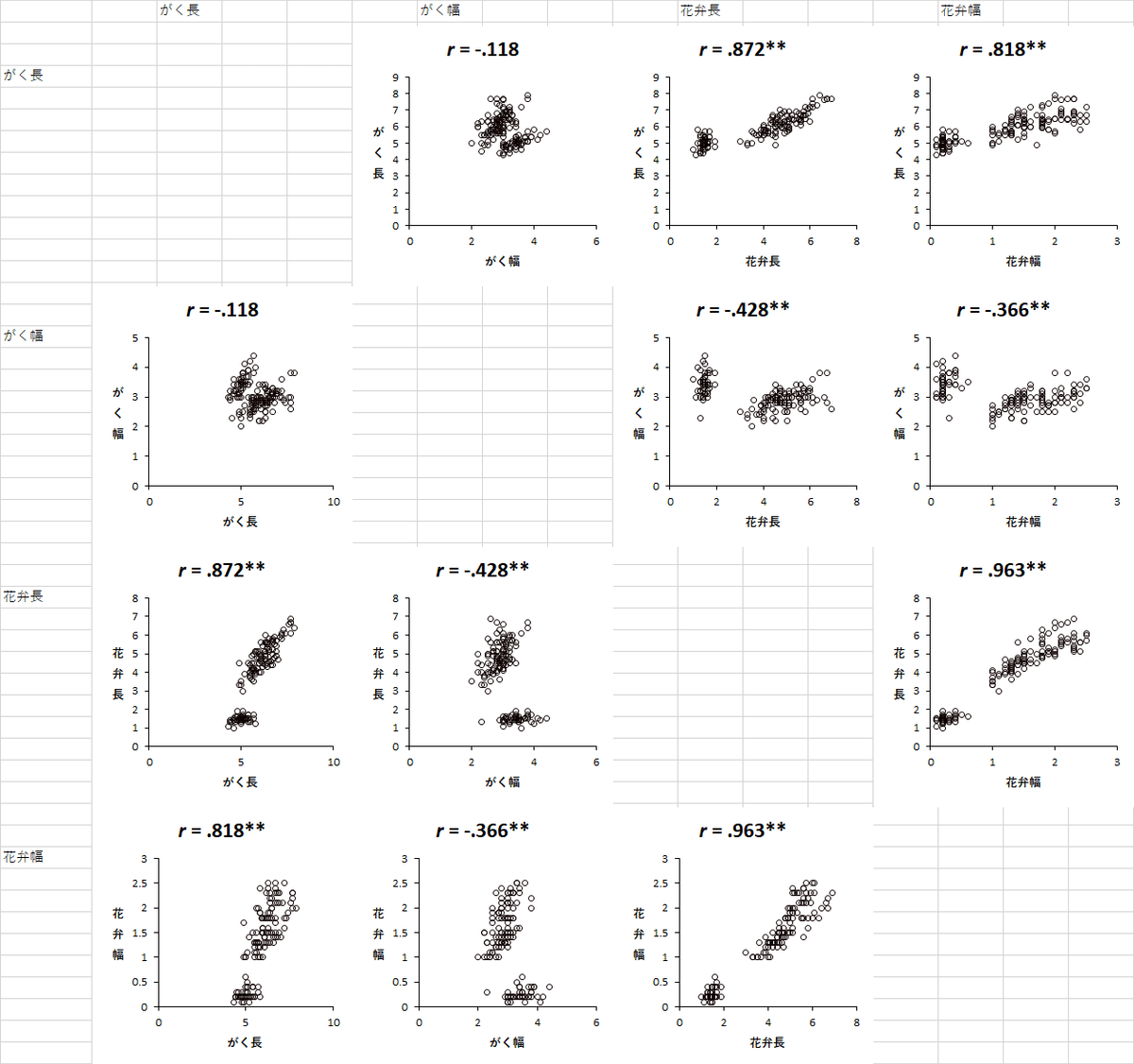
N2セルには「0.18秒」とありましたから，あっという間に分析は終わっているはずですが，いかんせん，プロットを作成して並べるという作業に時間がかかるのでしょう，体感では10秒近く待たされました。すべての組合せの散布図が並んで，相関係数が算出されて，検定結果（記号だけですけど）も表示されて，完璧，とか思えますが，HADの実力はこんなものではない。
変数どうしの関係に興味のあるペアを特定したら，基本通り，２つの変数だけで同じ分析を行います。ここでは，がく長，がく幅のペアを選びました。出力はこんな感じ。

相関係数は -.118 で，この分析では有意な係数ではありませんでした。HADでできること一覧にも書かれているとおり，「直線への当てはまり」つまり一般的な回帰分析もしてくれるところが，なんとも親切ですねえ。相関係数と回帰係数の関係とか，相関係数と決定係数との関係とか，統計学の試験に出そうですもんね。

グループごとの散布図

とはいえ，iris データには３つの「種」が含まれていますから，種ごとに分けてみたら，有意な相関がみつかるかもしれない。そこで登場するのが，さきほどの「グループ別」オプションですね。手順は，

散布図を描きたい変数を２つ指定，グループが入力された変数を１つ指定⇒【分析】⇒「散布図」と「グループ別」にチェック。

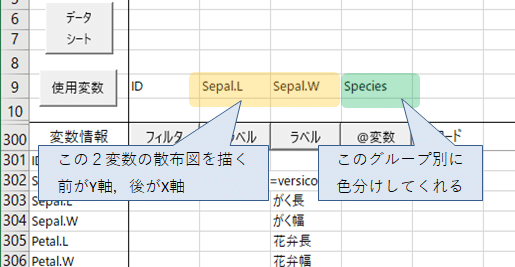
これ大事なのは，変数の数を守ることで，たくさん変数を並べても，最初の２つの変数の散布図を描いて，３つめの変数でグループ分け（色分け）します。３つめに連続変数なんぞ指定すると妙なものが出力されますから注意。

そういえば，変数の指定で，前の変数が散布図のY軸側に，後ろの変数がX軸側になります。相関係数を見たいだけならどっちでもいいんですが，回帰分析では順序が重要。後ろの変数（X軸側）が「独立変数（説明変数）」で，前の変数（Y軸側）が「従属変数（目的変数）」。なので，「がく長」「がく幅」の順番で変数を並べると，後ろが独立変数なので，（正の相関があると仮定すれば）「がくの幅が広くなれば，長さも長くなるだろう」という仮説や期待をもって分析していることになる。独立とか従属とか，設定順序とか，統計ソフトをさわり始めたころは本当に混乱しました。まあ，慣れるしかないのですけどね。では，出力の結果。

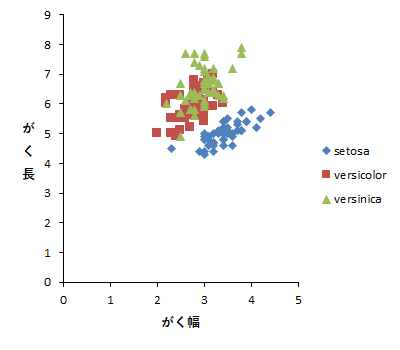
散布図が，Species（種）ごとに色分けされていて，よく見ると，それぞれの種のなかでは，プロットは右上がりの配置になっているようです。つまり，さきほどの -.118 という相関関係は，３つの異なる種が混在していたために，ごく弱い負の相関があるように見えただけで，種ごとでは正の相関がありそう。
しかし，注意したいのは，相関係数などの分析結果は，種ごとに分けて分析してくれているわけではなく，つまり「グループ別」は，あくまでも散布図の表現についてのみであって，相関係数はグループ別になっていない。回帰分析も同じ。うーむ。やや残念感がある。

by フィルタを使う

そこで，by フィルタを使う。by フィルタは，グループ別に，同じ分析を繰り返しやってくれるというオプションで，HADの強力な機能のひとつだと，わたしは思います。今回は散布図に対して使いますが，他の分析にも使えます。手順は，

散布図を描きたい変数を２つ指定⇒Species の行の「フィルタ」の下に「by」と入力⇒【分析】⇒「散布図」にチェック。

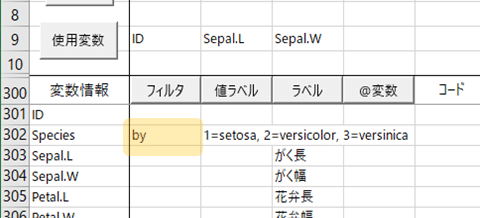
気を付けることは，さきほど設定したグループ変数（Species）を使用変数から除外することと，「グループ別」オプションにチェックしないことです。「by」（半角ね）の入力位置は図の通り。「フィルタ」ボタンをクリックしてGUIで設定してもよし。

これで実行すると，「Scatter_bysetosa」「Scatter_byversicolor」「Scatter_byversinica」の3つのシートが作られて，それぞれ，該当する種のデータだけを使った，がく長とがく幅の散布図が描かれます。下の図は，３つのシートを1つにまとめたものです（少し情報を間引き，文字色やセル背景色，太字などをあとから追加しています）。予想通り，種ごとに分けると，がく長とがく幅には有意な正の関係がみとめられました。

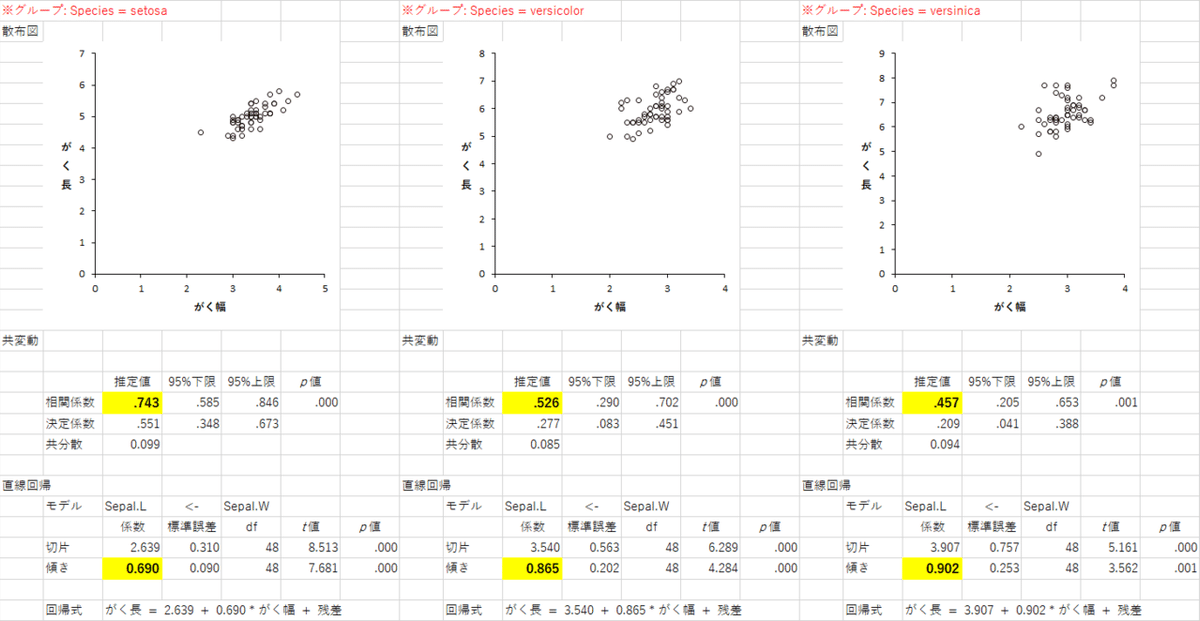
HAD2R 散布図

さて，散布図のHAD2Rは次のようなコードを出してくれます。まず変数3つ以上の場合。

subdat <- subset(dat, select = c(Sepal.L,Sepal.W,Petal.L,Petal.W))
plot(subdat)

これを実行すると，こんなプロットが描かれます。

もちろんですが，出力されるのはプロットだけで，相関係数を出したいときには別の手順が必要です。たとえばこんな感じ。

HAD2Rが出してくれるコードは，変数が2つのときも，3つ以上のときも実は同じです。変数が2つのときは，

subdat <- subset(dat, select = c(Sepal.L,Sepal.W))
plot(subdat)

で，Rのプロットはこんな感じです。

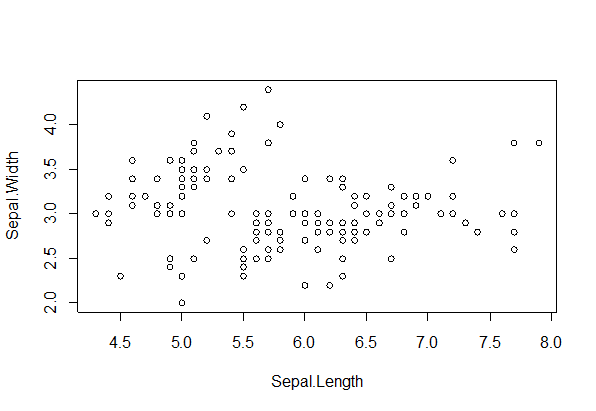
軸の目盛りの設定が違うので見た目がかなり違いますねえ，中身は同じですけど。と思いきや，よーく見ると，（上の方の，色分けしたプロットと見比べよう！）X軸とY軸が入れ替わっていますね。HADでは，先に指定した変数がY軸に設定されますが，RではX軸です。Rのコードでは見えにくいのですが，subset 関数に変数を指定するとき，Sepal.L が先になっているので，次の行の plot 関数は，plot(dat$Sepal.L, dat$Sepal.W) と同じ意味になっています。これ，ちょっと盲点ですね。相関関係をみているので，X軸とY軸は，どっちでもいいといえばいいのですが，やはりX軸側の変数を「原因」，Y軸側の変数を「結果」として，「Xが増えるとYも増えるよね」みたいについ言葉で考えているので（少なくともわたしは，そうです），それが逆になることで，単純な勘違いを生む原因になりかねません。なので，どこかで変数を入れ替える必要がある。方法は3種類あるけど，どれも似たようなもの。

１：subdat <- subset(dat, select = c(Sepal.W,Sepal.L))
２：plot(subdat$Sepal.W, subdat$Sepal.L)
３：plot(y = subdat$Sepal.L, x = subdat$Sepal.W)

そうすると，HADのプロットと同じ配置になります。でもね，ことはそう簡単ではなくて，変数が3つのときや4つのときには，単純に前後を入れ替える，なんてことはできません。入れ替えなくても，HADとRのプロットは（軸の目盛りの設定が違うだけで）同じ配置になっています。問題になるのは2つの変数のときだけです。ああ，ややこしい。はい，次。

HAD2R 相関係数と直線回帰とbyフィルタ

HAD2Rが出してくれるRのコードには，相関係数の算出や直線回帰などは含まれませんから，追加のコードが必要です。でもその前に，ちょっと問題がありますよ。

byフィルタをつけた状態でHAD2Rをオンにすると，どうも，必ずエラーが出るようなのです。おや大変。
このbyフィルタというのは結構強力なフィルタだとすでに書きました。要約統計量や箱ひげ図でも当然使えるのだけど，「群ごとの統計量」という分析メニューがあるので実際にはあまり使わなかったりする。でも，群ごとに相関係数まで見たい，というときにはbyフィルタが有用です。でも，byフィルタを設定したまま分析すると，こんなエラーが。

このエラー表示は，分析方法を「要約統計量」や「箱ひげ図」に変えても同じのが出るので，HAD2R＋byフィルタの設定のときに，どこかで不具合が生じているようですね。残念。

で，要するにHADの出力と同じ内容のものを出せばいいだろう，という感じでコードを書くと，こんな感じです。これはbyフィルタありの場合に対応するコードで，フィルタなしの場合は for の中だけを（適宜変更しつつ）1回だけ実行すればよし。

# 相関係数の検定をしてHADと同じ出力をする関数
# y,x 相関係数を算出したい変数（ベクトル）Y軸側，X軸側
hadlike_cor_test <- function (y, x) {
 res <- cor.test(x, y)
 covar <- var(x, y)
 
 # 決定係数の信頼区間算出がわからないので空白
 d <- c(res$estimate, res$`conf.int`, res$`p.value`, 
        res$estimate ^2, NA, NA, NA, covar, NA, NA, NA)
 m <- matrix(d, ncol=4, byrow=T)
 # 決定係数の信頼区間算出がわからないので空白
 colnames(m) <- c("推定値","95％下限","95％上限","p値")
 rownames(m) <- c("相関係数", "決定係数", "共分散")
 # 四捨五入したほうがdig=3よりも桁が揃えやすい。
 print(round(m,3), na.print="")
}

# 直線回帰分析をしてHADと同じ出力をする関数
# y, x 回帰分析したい変数（ベクトル）Y軸側（独立変数），X軸側（従属変数）とそのラベル
hadlike_lm <- function (y, x, ylab="Y", xlab="X") {
 mdl <- summary(lm(y ~ x))
 
 df <- data.frame("est"=c(0,0), "se"=0, "lower"=0, 
                  "upper"=0, "df"=0, "t"=0, "p"=0)
 df[,c(1,2,6,7)] <- mdl$coefficients[1:2,1:4]
 df$df <- mdl$fstatistic["dendf"]
 # まとめてやろうとしたけど，失敗したので順番に
 df$lower <- df$est + df$se * qt(p=0.025, df=df$df)
 df$upper <- df$est + df$se * qt(p=0.975, df=df$df)
 # 最初からこの列名でdfを作ると"95％"がうまく入らない
 # あと,その後の計算式に漢字が出てくるのがいやだ
 colnames(df) <- c("係数","標準誤差","95％下限",
                   "95％上限","df","t値","p値")
 rownames(df) <- c("切片","傾き")
 cat(paste("モデル：", ylab, " ← ", xlab, "\n", sep=""))
 print(round(df, 3))
}

# グループ分けの変数を factor 型にして
dat$Species <- as.factor(dat$Species)
levels(dat$Species) <- c("setosa", "versicolor", "versinica")

# グループの数だけループする
for (g in levels(dat$Species)) {
 d0 <- dat[dat$Species==g,]
 cat(paste("\n", "グループごとの分析 :", g, "\n", sep=""))
 plot(d0$Sepal.W, d0$Sepal.L, main = paste("Group : ",g))
 hadlike_cor_test(d0$Sepal.W, d0$Sepal.L)
 hadlike_lm(d0$Sepal.W, d0$Sepal.L, "Sepal.W（がく長）", "Sepal.L（がく幅）")
}

長い。長いけど，エラー処理とか書いてないし，欠損値があるときどうするとか考えてない。byフィルタがあるときとないときと分岐するべきコードも書いてない。まあ，しょせん趣味なので。結果はこんな感じ。出力も長いので初めの方だけ。（散布図は省略）

これをHADに実装してほしいかというと，やはりそれは別の話でしょうね。この分析でグループに指定している Species は，1,2,3 という素直な（？）数値なので問題が起きにくいだけかもしれない。ソフトからコードを吐かせるとしたら，どんなデータにも対応できないとだめだろうし。そういう手間を考えると，ヒントの提示，くらいにとどめておいていいだろうと思います。今回は関数まで書いてしまいましたが，cor.test 関数と lm 関数（と summary 関数）と並べておくだけでもいいし。この関数を使えば同じような分析できるよ，という道筋を示すことは意味があると思います。

少々残念な感じのエラーも出てしまいましたが，R のデータ処理の練習になりました。回帰係数の信頼区間の計算もちゃんとできたし。HAD と数値が一致したので「あってる！」と思えました。清水先生に答え合わせしていただいている感覚ですね。でも，決定係数の信頼区間ってどう計算するのでしょう。誰か教えて！