総和記号って知ってる?
はじめまして、Σです。
$${\sum}$$(総和記号、Σ)にはじめて出会うのは、どうやら高校数学らしいのですが、私は全く記憶にありません。現行の学習指導要領では、「数学B」で扱うことになっているようです。ふむ。私の頃は「数学ⅡB」とか言っていた気がしますが、このあたり、芳沢先生がずいぶん批判しておられるので、お任せしたいと思います。
さて、いかつい顔をしている$${\sum}$$ですが、要するに足し算の記号です。足し算は「+」の記号を使って書けるのですが、数列の和など、「いくつあるかわからないけど、全部足す」という計算を書き表そうとすると、こういう記号を使わざるを得ないという事情があるようです。
統計の場合も同じで、具体的にデータを集めた後はもちろん、いくつあるかわかっていますが、理論の話をするときには、$${n}$$個足す、みたいな書き方をする必要があるので、こうなっているようです。
おしゃべりはさておき。
演習課題
E1:次のデータ $${x=(2,6,7,10,15), m=8}$$ について、下に示した計算をしてください。
(1) $${\frac15\sum_{i=1}^5 x_i^2}$$
(2) $${\frac15\sum_{i=1}^5 (x_i-m)}$$
(3) $${\frac 15\sum_{i=1}^5 (x_i-m)^2}$$
(4) $${\big\{\frac15\sum_{i=1}^5 x_i^2\big\} - m^2}$$
E2:E1の計算結果から、気づいたことを述べてください。
E3:上の計算式で、$${c=7}$$ や $${c=9}$$ のとき、b、c、dの計算結果がどう変わるか試してみましょう。
数式が苦手な方には、ちょっと難しい課題だったかもしれませんね。以下、解答例です。
解答例
E1:計算結果は次のようになります。
(1) $${\frac15\sum_{i=1}^5 x_i^2 = \frac15(2^2+6^2+7^2+10^2+15^2)=\frac15\times414=82.8}$$
(2) $${\frac15\sum_{i=1}^5 (x_i-m)=\frac15\{(2-8)+(6-8)+(7-8)+(10-8)+(15-8)\}=\frac15(-6-2-1+2+7)=\frac15\times0=0}$$
(3) $${\frac 15\sum_{i=1}^5 (x_i-m)^2=\frac15\{(2-8)^2+(6-8)^2+(7-8)^2+(10-8)^2+(15-8)^2\} = \frac15(36+4+1+4+49)=\frac15\times94=18.8}$$
(4) $${\big\{\frac15\sum_{i=1}^5 x_i^2\big\} - m^2=82.8-64=18.8}$$ (中カッコの中は(1)で計算しています)
E2:式の形は異なるのに、なぜかcとdが同じ計算結果になることには気づいていただきたいです。
ほかにも気づきはあると思います。それぞれの気付きを大切にしてください。
E3:計算回数が多くなりますので、Excelに任せることにします。次のようになります。
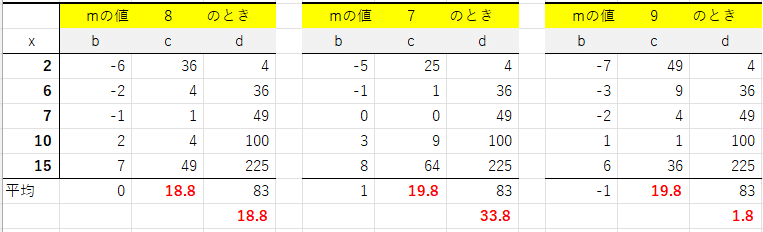
bの計算結果:mの値が1だけ変化すると、bも1だけ変化しました。mの値の増減と、bの計算結果の増減が逆方向になることが興味深いですね。
cの計算結果:どちらも1だけ変化しました。mの値の増減にかかわらず、cの計算結果が1だけ大きくなっていることもまた、興味深いですね。
dの計算結果:bやcとは異なり、大きく変化しました。表を見ると、$${x^2}$$の平均が全く同じなのに、mの値だけが変化するのでこのようになることがわかります。
お気づきでしょうが、最初に設定した$${m=8}$$は、$${x}$$の平均値です。mがデータの平均値と一致するときだけ、式cとdの計算結果は等しくなるのです。また、cの式は、後に学習する分散の定義式、dの式は、手計算で分散を計算するときの式(分散公式)です。すでに他の教科書や参考資料などで、お目にかかった方もいらっしゃるでしょう。この公式について、もう少し詳しく勉強してみたい方は、次のスライドをご参照ください。
