HADを使ってみた：11.t検定

2021年2月16日 22:58

前回書いたように，HADの分析メニューには「t検定」という言葉は出てきません。「平均値の差の検定」で，独立変数が2水準であるとき，t検定が行われ，3水準以上なら分散分析が行われます。出力内容がまったく違うので，今回はt検定のみです。

t検定と分散分析

統計を学び始めた頃「分散分析」という分析方法がどうも頭に入っていなくて，いわゆる「等分散の検定」こそが分散分析なのだと信じ込んでいた時代がありました。懐かしい。しかし，平均値の差の検定，というまとめ方からわかるように，両者は水準数が異なるだけで同じ目的の分析ですね。帰無仮説は「すべての水準で平均値に差はない」という感じになります。清水先生の説明を引いておきましょう。

基本的にはt検定も1要因分散分析もやり方は同じです。t検定には、よく知られているように対応のないt検定と、対応のあるt検定があります。これはそれぞれ、分散分析でいうところの、１要因参加者間計画と１要因参加者内計画にあたります。ただし、水準数が２水準である場合に限ります。実際、ｔ検定で得られる自由度（N-1）のｔ値は、１要因２水準の分散分析における、自由度（1,N-1)のF値の平方根に一致します。確率も同じです。（太字は引用者，https://norimune.net/648）

この太字部分を知ったときにはとても新鮮な気持ちでした。その後，南風原先生や吉田先生の本を読むに至って，ばらばらだった統計の知識が少しずつですが，つながりを持ち始めたように思います。

d効果量

ところで，t検定の結果出力で，気になるのはやはり効果量です。HADでt検定の出力をすると，こんなふうに効果量が出力されます。データは iris で，従属変数は Sepal.L（がく長），独立変数は Species（種）で，Species が1と2のデータだけ（setosa と versicolor）を用いています。

効果量dは，統計の教科書にもよく登場しますね。きわめてざっくりいうと，平均値の差が，標準偏差のいくつ分くらいあるか，を示した数値です。この場合は絶対値が２を超えていますから，2つの種の間で，平均値の差が標準偏差の2倍以上あるという，めちゃめちゃ大きな差です。しかし，rってなんでしょう。平均値の差の検定の文脈でr効果量に出会うのは，正直言ってHADが初めてです。水本 & 竹内（2008）によれば，

だそうです。実際，Species（ここでは1と2という数値が使われていますね）と，Sepal.Lとの相関係数を計算すると，HADが出力する値に一致しますので，通常の相関係数と同じ計算をしていると思われます。
水本 & 竹内論文はこちら。

dなのかgなのか

もう一つ気になるのは，効果量の名称（？）というか，記述するときの文字が，d なのか g なのかということですね。d は Cohen の d として言及されることもありますが，報告されている数値は実際には Hedges' の g だとか，効果量について書かれた論文を読んでいると，かなり頭が混乱することもあるのです。清水先生の説明を見ておきましょう。

ｄ族の効果量とは，Cohenのdをはじめ，2群の平均値の差を標準化した効果量のことです。（中略）Cohenが提案したdは，記述統計学的な意味で計算された効果量で，母集団の性質を推測する，推測統計学的な効果量ではありません。そこで，Hedgesは推測統計学的な意味で計算された標準化された差，gを提案しました。ただ，多くの論文では，gをdと表記して記載していることがほとんどです。（https://norimune.net/1512）

だそうです。しかし，この計算式がまたやっかいです。上で引用した記事で示されている式は，

この値で，両群の平均値の差を割るとｇが計算されます（つまり，両群の平均値の差÷プールされた標準偏差）。また，t値と両群の n を使った簡便な計算式も示されていて，それがこの式です。

式の引用はいずれも上で引用した清水先生のブログ記事（https://norimune.net/1512）です。実際，２つの式で計算される値は一致し，その値は，Rの effsize ライブラリにある cohen.d( ) 関数の出力と一致します。めでたし。といいたいところですが，なんと，HADの出力結果はこれと一致しません。

最初に引用した，HADが出力した d 効果量よりも，Rの出力の方が少し大きいことがわかります。この差は何？
実はこの関数には，hedges.correction というオプションがあり，TRUEを指定すると，Hedges の補正を行うと書いてあります。やってみると，

これはHADの出力と一致するのですね。信頼区間が微妙に異なるのが気に入らないのですが，少なくとも推定値は一致しました。むむ？　何がどうなっているのやら。

あらためてdを調べてみる

あらためてネットを検索してみると，西井淳氏のサイトが見つかりました。

ここに，効果量についてのわりと詳しい説明があります。そこで西井氏が参照している，Nakagawa & Cuthill (2007)も参照しながら，d効果量について整理しておきます。

Nakagawa & Cuthill (2007) によれば，まず，d効果量を計算する式は，

この式で，これは清水先生がブログで示している式と同じものです。これが d を計算する式であり，この式で算出される値が，Cohen's d あるいはHedges' g，あるいは単に d，標準化平均値差などと呼ばれている，と書いてあります。上記の表の注に，こんな文章があるのです。

Strictly speaking, Equations 1 to 4 are for Hedges’s g but in the literature these formulae are often referred to as d or Cohen’s d while Equation 10 is Cohen’s d.

なんだ，やっぱりこれでいいんじゃないかと思いきや，この算出方法ではバイアスがあるので，次の式で補正すると書いてあります。

Nakagawa & Cuthill (2007) によれば，これは，サイプルサイズが小さいときに（目安としてN=20），バイアスを補正するものだと書いてあります。この式で補正されたものは，Hedges' d（Unbiased Cohen's d or Hedges' g）と呼ばれていると。そしてその直後には，サイプルサイズが大きくなれば，補正は小さくなるので，効果量の計算手順に機械的に組み込むことを推奨する，と書いてあります。

It is recommended that this correction be used routinely, although bias is negligible when sample size is large. (p. 599)

ただし西井氏の記事では，＝ではなく≂（ニアイコール）が用いられており，あくまでも近似値であるというのが西井氏の解釈なのかもしれません。論文の後半には，効果量の標準誤差と信頼区間についても説明がありました。
とまあ，西井氏がまとめてくださっていることをそのまま繰り返しただけなのですが，いちおう，もとの論文にあたって確かめたぞ，ということを書いておきたかったわけです。では，Rで計算してみましょう。

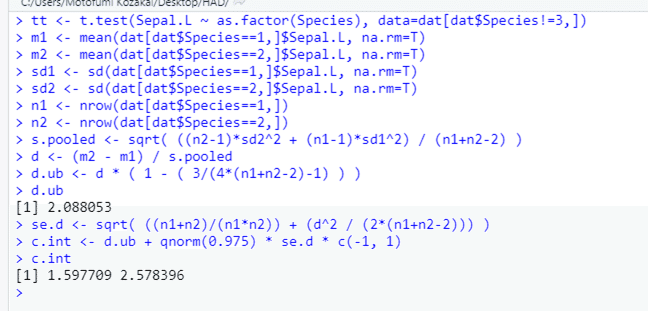
ということで，Nakagawa & Cuthill (2007) に基づいて計算した結果は，R の effsize ライブラリの cohen.d( ) 関数で，hedges.cor = T オプションを指定して計算した結果と一致しました。正確には，効果量の推定値は等しく，信頼区間はやや広くなっていました。しかし，信頼区間の幅の違いは 0.01 以下ですので，実質的な問題とはいえないでしょうね。HADの計算結果と比較すると，やはり推定値は等しくなったのですが，信頼区間は広くなっていました。cohen.d( ) に比べてもHADの信頼区間は狭く，いろいろ試したうちで最も狭い信頼区間を示していました。とはいえ，実質的に問題になるほどの差ではないでしょう。信頼区間の幅の違いについては，ちょっと私の手には負えないところにありそうです。

複数の分析を一度に

さて，どうしても書いておきたいことは，HADでは複数のt検定を一度に実行できる機能がある，ということです。書式はこんな感じ。

使用変数を設定：従属変数（複数可），独立変数（１つ）
⇒【分析】
⇒「平均値の差の検定」
⇒「対応なし」を選択（デフォルト）

たとえば iris データだと，がく長も，がく幅も，花弁長も，花弁幅も，どれも種によって違いがありそうですから，従属変数に「がく長，がく幅，花弁長，花弁幅」と設定，その右に独立変数として「種」を設定すると，「がく長 ~ 種」，「がく幅 ~ 種」，「花弁長 ~ 種」，「花弁幅 ~ 種」の4種類の検定を一気にやってくれるということなのですね。出力シートが一気に4枚できます。

そういえば，Rを使い始めた頃に，この「~」（チルダ演算子）がなかなか覚えられず，どっちが独立変数なんだ？　とか，そもそも従属変数と独立変数はどっちが何の役割なんだ？　とか，いろいろ混乱していた時期がありましたね。で，結局，「身長 ~ 性別」というような式なら，「身長を性別ごとに比べる」みたいな日本語に翻訳して，だんだん慣れてきたのでした。なので，「がく長 ~ 種」だったら「がくの長さを，種ごとに比べる」とか，「がくの長さって，種ごとに違うんじゃないの？」みたいな文に翻訳して，有意差があったら，「やっぱり違うらしいねえ」という結論に翻訳する，みたいな感じでよいかと。もちろん，統計的仮説検定で p<.05 になっても，それは「差がある」と胸をはっていえるわけではない，ということも，同時に理解していく必要があるんですけどね。

HAD2R：t検定バージョン

さて，t検定のときに HAD2R が出力するコードに全角の「～」が含まれてしまっていることは前回書きました。いずれ改善されると思いますが，直っていないバージョンだったら気をつけましょう。今回も，HADの結果を再現できるようにコードを書き加えてみましたが，なにせ，量が多い，効果量の出力結果がどうも合わない，意味のよくわからない出力がある，など，いろいろとあって困りました。なので，理解できてコードが書けた分だけ，残しておくことにしましょう。

意味のよくわからない出力とは，最初に示した出力例の一番下にある，「Prep = 1.000」です。これ，何なんですかあ？　知っている方は教えてください。

ha
dlike_t_test <- function(d0, levstr=paste("Level-",1:2, sep="")) {
 # 独立変数の列数と水準数を確認，因子型に変換し2水準でないならエラー
 d0 <- na.exclude(d0)
 if (length(d0)!=2) {
   cat("エラー：引数は従属変数と独立変数のみの2列のデータである必要があります。\n")
 }
 else {
   d0[,2]<-as.factor(d0[,2])
   if (length(levels(d0[,2]))!=2) {
     cat("エラー：独立変数の水準数は2である必要があります。\n")
   }
   else{
     # 水準ごとの統計量の算出
     d1 <- hadlike_summary(d0, levstr)
     # プロット
     barplot(d1$Mean, space=c(0.5,0), xlim=c(0,4), 
             ylim=c(0,ceiling(max(d0[,1]))), 
             xlab=colnames(d0)[1], ylab=colnames(d0)[2], col=c(0,8))
     legend("right", legend=levstr, fill=c(0,8))
     arrows(c(1,2),d1$Mean-d1$StdErr, c(1,2), d1$Mean+d1$StdErr, code=3, lwd=1, angle=90, length=0.1)
     abline(0,0)
     # Welch検定とt検定，プロットの描画
     d2 <- hadlike_welch_t(d0)
     # 効果量の算出
     d3 <- hadlike_cohen_d(d0, d1, d2)
   }
 }
}

# 水準ごとの統計量の算出
# 引数　d0 : データフレーム，第1列が従属変数，第2列が2水準の独立変数
# 戻値　d1 : 統計量データフレーム
hadlike_summary <- function(d0, levstr) {
 # 要因ごとの統計量
 d1 <- data.frame("mean"=c(0,0), "sd"=0, "se"=0, "lw"=0, "up"=0, "n"=0)
 d1$mean <- tapply(d0[,1], d0[,2], mean, na.rm=T)
 d1$sd <- tapply(d0[,1], d0[,2], sd, na.rm=T)
 d1$n <- tapply(d0[,1], d0[,2], NROW)
 d1$se <- d1$sd / sqrt(d1$n)
 d1$lw <- d1$mean - d1$se * qnorm(0.975)
 d1$up <- d1$mean + d1$se * qnorm(0.975)
 colnames(d1) <- c("Mean", "SD", "StdErr", "95%CI-lower", "95%CI-upper", "N")
 row.names(d1) <- levstr
 cat("\nSummary by Levels\n")
 print(round(d1, 3))
 return (invisible(d1))
}

# 2種類の検定統計量 1:Welch-test, 2:t-test
# 引数　d0 : データフレーム，第1列が従属変数，第2列が2水準の独立変数
# 戻値　d2 : 検定統計量と検定結果データフレーム
hadlike_welch_t <- function(d0){
 d2 <- data.frame("dif"=c(0,0), "se"=0, "lw"=0, "up"=0, "t"=0, "df"=0, "p"=0)
 t1 <- t.test(d0[,1] ~ d0[,2], var.equal = F)
 t2 <- t.test(d0[,1] ~ d0[,2], var.equal = T)
 d2$dif <- c(t1$est[1]-t1$est[2], t2$est[1]-t2$est[2])
 d2$se <- c(t1$stderr, t2$stderr)
 d2$t <- c(t1$statistic, t2$statistic)
 d2$df <- c(t1$parameter, t2$parameter)
 d2$p <- c(t1$p.value, t2$p.value)
 d2[,c("lw","up")] <- d2$dif + d2$se * qt(p = 0.975,df = d2$df) * c(-1,1)
 colnames(d2) <- c("Difference", "StdErr", "95%CI-lower", "95%CI-upper", "t-value", "df", "p-value")
 row.names(d2) <- c("Welch-test", "Student t-test")
 cat("\nt Test\n")
 print(round(d2, 3))
 return (invisible(d2))
}

# 効果量の算出
hadlike_cohen_d <- function (d0, d1, d2) {
 d3 <- data.frame("est"=c(0,0), "lw"=0, "up"=0)
 # r 効果量：2列目が数値データでないとうまくいかない
 r <- cor.test(d0[,1], as.numeric(d0[,2]))
 d3[1, 1:3] <- c(r$est, r$conf[1:2])
 s.pooled <- sqrt( ((d1$N[2]-1)*d1$SD[2]^2 + (d1$N[1]-1)*d1$SD[1]^2) / (sum(d1$N)-2) )
 d <- (d2$Difference[1]) / s.pooled
 d.ub <- d * ( 1 - ( 3/(4*(sum(d1$N)-2)-1) ) )
 se.d <- sqrt( ((sum(d1$N))/(d1$N[1]*d1$N[2])) + (d^2 / (2*(sum(d1$N)-2))) )
 c.int <- d.ub + qnorm(0.975) * se.d * c(-1, 1)
 d3[2, 1:3] <- c(d.ub, c.int[1:2])
 colnames(d3) <- c("Estimate", "95%CI-lower", "95%CI-upper")
 row.names(d3) <- c("r", "d")
 cat("\nEffect Size\n")
 print(round(d3, 3))
 return(invisible(d3))
}

いやあ，長い。効果量のところでけっこう苦労したので，かなり気合を入れて関数にしてしまった。出力結果はこんな感じです。当初，psych ライブラリを使って書いていたのですが，効果量のところでライブラリを使わずに式を書いたので，統計量の部分もそれに準じました。