
HADを使ってみた:7.クロス表
今回はクロス表です。クロス表を作成するからには,カテゴリ変数が複数必要なので,今回は iris ではなく,HAD_sample_data.xlsx から「factor」を用いることにします。本来は,因子分析の説明のためのデータだと思われます。とりあえず要約統計量を見てみましょう。
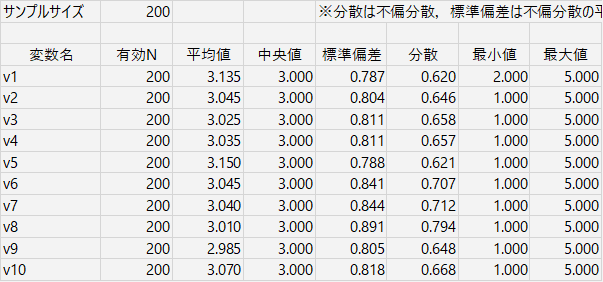
v1 だけ最小値が2ですが,あとは1~5の範囲で,中央値は3,平均値もほぼ3ですね。標準偏差は0.8前後ですので,2~4のあいだに多くのデータが集まっている感じでしょう。より詳しくは,正規性検定や度数分布表などで確認することになりますが,今回は省略。
クロス表を作る
データを観察したところで,クロス表の作成に移ります。クロス表と言っても,実際によく使われるのは2×2のクロス表でしょう。ここでは v1 と v2 を使います。手順は簡単で,
クロス表を作成したい2つの変数を指定
⇒【分析】
⇒「クロス表」または「バブルチャート」
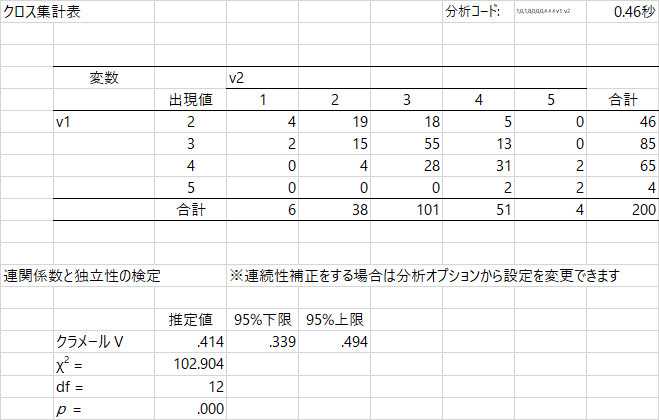
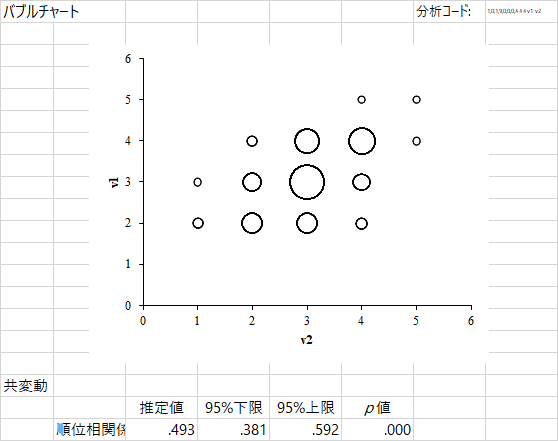
出力されるのはこんな感じですね。HADでは1番目の変数が列,2番目の変数が行です。バブルチャートを見ると,散布図のときと同じ位置関係です。バブルチャートは,クロス表のセルごとの数値の大きさを,円の大きさで表現しているので,視覚的に特徴をつかむことができる。このチャートだと,どちらの変数も値が2~4に集中していて,両方とも3である場合がもっとも多いことがわかります。バブルチャートは「順位相関係数」も出力してくれますが,これは分析メニューにいずれ出てくるので,今回はパスしましょう。
実は清水先生のブログ記事の中で,クロス表はわりと数多く言及されています。私が整理した限りでは7回。それによれば,HADのクロス表の特徴は次の点かと思われます。
●クロス表をデータとして入力できる(https://norimune.net/674)
●クロス表の残差分析ができる(https://norimune.net/712)
●5変数までの多重クロス表を作成できる(https://norimune.net/698)
では,順番に。
データとしてのクロス表
前述の記事によれば,
手元にクロス表しかないような場合でもポリコリック相関や順位相関、連関係数などが計算できるようになりました。また、対応分析もクロス表から分析可能です。(https://norimune.net/674)
とあります。せっかくなので,さっきとは別のクロス表データを入れてみましょう。放送大学のサイトで,入学者数統計を見ることができます。2007年度から2020年度まで,学期別,学生種別の人数が公開されていますので,ここでは各年度の1学期の入学者数をデータとして使いましょう。
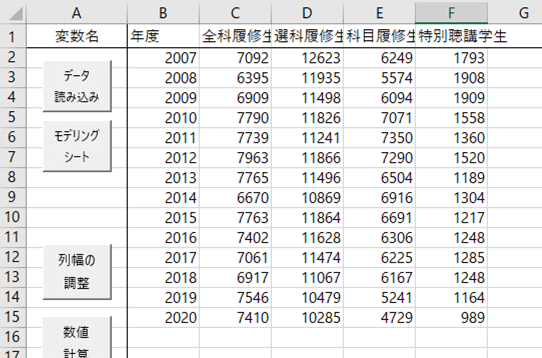
【データ読み込み】して,使用変数に,4つの学生種を設定し,【分析】クリック。ここで重要なのは,左上の「クロス表として読み込む」というオプションを選択することですね。クロス表をそのまま入力してできる分析は限られていますから,ほとんどの分析メニューはグレーアウトします。クロス表にチェックして実行。
出力されるのは,まず,入力されたものと同じクロス表と,連関係数,そして独立性の検定です。連関係数はほぼ0ですので,有意な連関はないといえます。クラメールの連関係数は値が0以上1以下にしかならないので,相関係数の信頼区間のように「0を含んでいるかどうか」という判断はできません。χ二乗値は有意なので,どこかのセルの値が有意に大きく,どこかのセルの値が有意に小さいということです。ただし,観測度数が大きければ検定が有意になりやすいのは当然の話なので,実際に意味のある差であるかどうかは,検定結果だけでは判断できませんね。
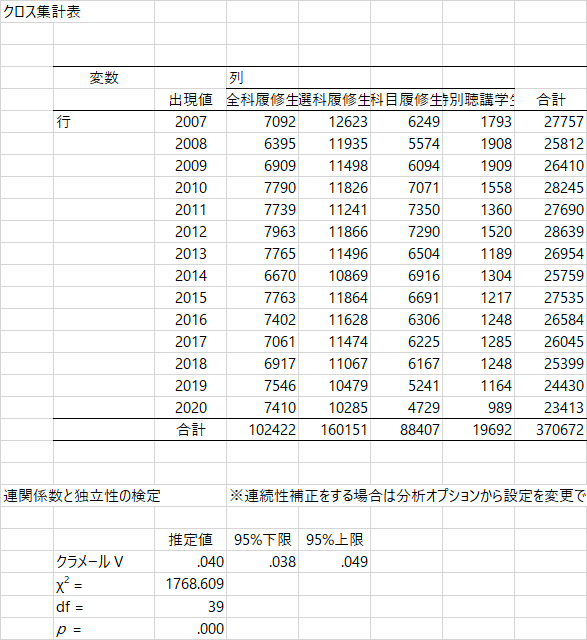
残差分析
クロス表分析の結果はとてもたくさんあって,検定の下には比率の表が3つ続きます。何が違うかというと,全体の合計を100%とするか(最初の表),行の合計を100%とするか(第2の表),列の合計を100%とするか(第3の表)。データの内容や分析の視点によって役立つ表は異なるかもしれません。ここでは第2の表に注目すると,「選科履修生」がつねに40%以上であること,特別聴講生はおおむね5%前後ですが,2008年と2009年では7%を超えていますね。統計的に意味のある差なのでしょうか。
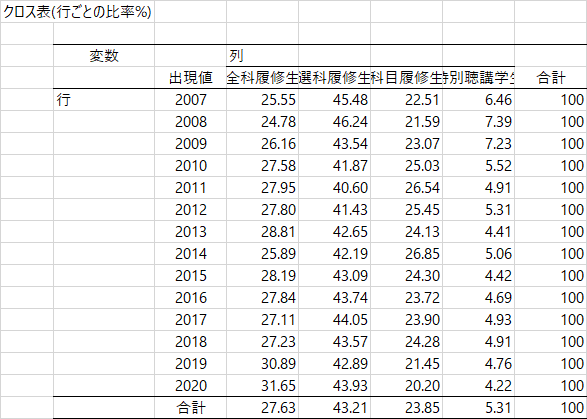
そのことを分析してくれるのが「残差分析」です。独立性の検定で有意なχ二乗値が出ても,どこのセルに有意差があるかはわからない。計算の仕方は,たとえば大学院科目「心理・教育統計法特論」(主任講師/小野寺孝義)で講義されていますよ。
余談ですが,この教科書の相関係数の算出法の説明は秀逸だと思います。2021年には科目が改訂されます。楽しみですね。
比率の表に続いて,3つの表があります。まず,どのセルが有意に多いか少ないかを記号で表した表。やはり2009年までは特別聴講生が現在よりも多く,それに対して最近は全科履修生や科目履修生が増えているといえるでしょう。この判断のもとになっているのが,その下に表示される「標準化残差」とp値の表ですね。このデータでは度数が大きいので,参考程度に見ないといけないかな。
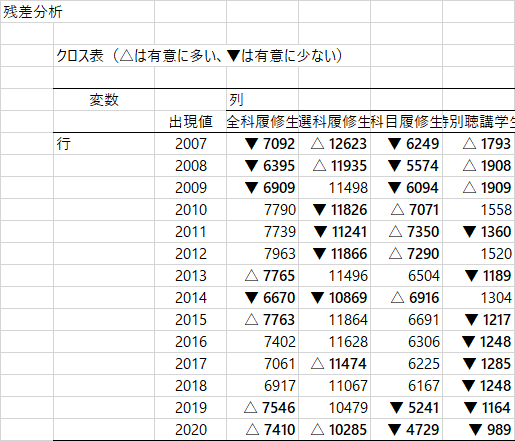
多重クロス表
最後に多重クロス表です。ふたたび factor データを用います。多重クロス表を実現する方法は2つあります。
一つは,散布図のときに使った「byフィルタ」を用いる方法です。たとえばさきほどの入学者数データだと,「学期」を変数に入れておいて,byフィルタを設定すれば,1学期と2学期とを別々に検討できます。ただし水準数の多いデータをフィルタにすると,シートがたくさんできるので,あとの整理が少々大変かもしれません。
もう一つの方法は,【分析】の「セルごとの度数」を用いる方法。これだと,5変数まで対応しています。やってみましょう。手順は,
クロス表を作成した変数を5つまで設定
⇒【分析】
⇒「セルごとの度数」
変数を6つ以上設定すると,エラーが出て止まりますよ。結果はこんな感じです。

それぞれの変数が4~5水準で,この表は2500行あります。度数が0の組合せもすべて出力されるので,実際には「度数」の行で降順ソートをして,どの組み合わせが多いかを見ることになるでしょうか。

この5つの変数だと,すべて3の組合せがもっとも多く,200人のうち19人がこの組み合わせになっていることがわかります。
連続性の補正について
そういえば独立性の検定における連続性の補正について後回しにしていました。設定手順は,
【HADの設定】
⇒【分析設定】
⇒「独立性の検定で連続性の補正を行う」にチェック
そうすると,たしかに結果は変わります。最初にやった v1 と v2 でやってみると,こんな感じ。
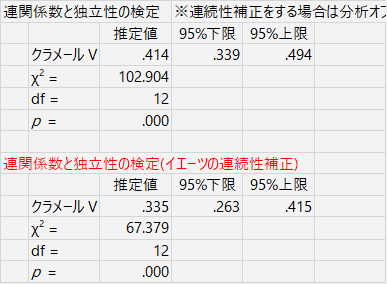
違うのはもちろん,この検定結果の部分だけで,作成される表はまったく同じです。残差分析も同じ。しかし,ここで言及されている「イエーツの連続性補正」は,2×2クロス表のときに使用される補正方法です。ネットで(ちょっとだけですが)調べてみてもやはりそう書いてあります。(上で検定している表は,df=12,つまり4×5の表です。)Rの独立性の検定でも,連続性補正は2×2のときにしか有効になりません。なので,ここで行われている補正がどのようなものか,私にはわからない。清水先生のブログでも,詳しい説明はないようです(見落としたか?)。
HAD2R バブルチャート
HAD2Rは,バブルチャートには対応していませんでした。これはちゃんとメッセージが出ました。

Rでむりやり出力しようとすると,ごく普通の散布図は出せますが,円の大きさをデータに応じて変える,ということは難しい。たぶん ggplot2 を使えばできそうな感じはしますが,うーむ。難しそうだ。
HAD2R クロス表
クロス表のRコードはかなりたくさん出てきます。こんな感じ。
dat <- read.csv("... /csvdata.csv")
tab <- table(dat$v1,dat$v2)
N <- sum(tab)
m <- min(length(table(dat$v1)),length(table(dat$v2)))
cramer <- (chisq.test(tab)$statistic / (N*(m-1)))^0.5
attr(cramer,"names") = "cramer's V"
tab
chisq.test(tab)
cramer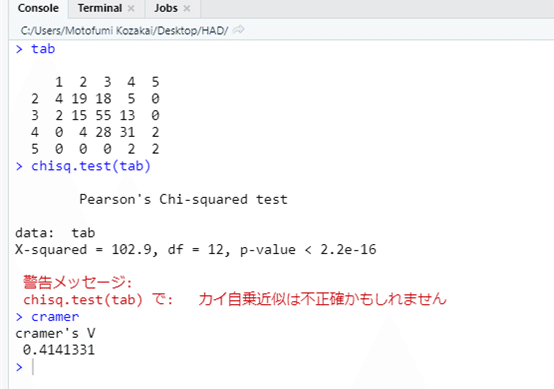
出力はこんな感じ。散布図のときはY軸とX軸が入れ替わっていましたが,クロス表では,列と行は入れ替わっていません。よかった。
コードの途中にある N も m も,クラメールの連関係数の算出に必要な数値を計算していますね。別のライブラリを使うとクラメールの連関係数を算出する関数もあるのですが,定義式のとおりに計算すると,ライブラリは不要だし,できるだけ基本的なライブラリだけで,という方針でしたし。
でも,比率の表くらいは出せるようにしたいなあと思いましたので,コードを少し追加してみました。標準化残差やp値も出せるので,それも追加しましたよ。
# HAD風 クロス表分析
# CC 連続性補正を行うか(実際には2x2のみ有効)
hadlike_cross <- function(tbl, CC = FALSE) {
CC <- FALSE # 連続性補正の設定
# Cramer's V 算出のために
nc <- sum(tbl)
m <- ifelse(nrow(tab)<ncol(tab), nrow(tab), ncol(tab))
x2 <- chisq.test(tbl, correct = CC)
crm <- (x2$statistic / (nc*(m-1)))^0.5
# クロス表
cat("\nクロス集計表\n")
print(addmargins(tbl, margin=c(1,2)))
# 検定
cat("\n連関係数と独立性の検定 \n")
cat(paste("クラメールのV:", round(crm,3), "\n"))
cat(paste("χ2 =", round(x2$statistic,3), "\n"))
cat(paste("df =", x2$parameter, "\n"))
cat(paste("p =", round(x2$p.value,3), "\n"))
# Fisher 検定
if (length(tbl)==4) {
cat("\nFisher の正確確率 \n")
ft <- fisher.test(tbl, alternative = "two.sided")
fl <- fisher.test(tbl, alternative = "less")
cat("両側確率=", round(ft$estimate, 3), "\n")
cat("片側確率=", round(fl$estimate, 3), "\n")
rm(ft, fl)
}
# 比率表
cat("\n全体に対する比率\n")
print(round(addmargins(prop.table(tbl), margin=c(1,2)), 3 )) # 全体
cat("\n行ごとの比率\n")
print(round(prop.table(tbl, margin = 1), 3)) # 行
cat("\n列ごとの比率\n")
print(round(prop.table(tbl, margin = 2), 3)) # 列
# 標準化残差と確率
cat("\n標準化残差\n")
print(round(x2$stdres, 3))
cat("\n p値\n")
print(round(pnorm(abs(x2$stdres), lower.tail = F)*2,3))
rm(x2, nc, m, crm)
}tbl <- table(dat$v1,dat$v2, dnn=c("v1", "v2"))
hadlike_cross(tbl)クラメールの連関係数の信頼区間算出だけわかりませんでしたので,空白。それにしても長い。わざわざ(?)関数にしておく利点は,コンソール出力に関数が表示されないので,きれい,という単純な理由ですね。あと,関数内で使った変数をクリアしておくのが一時期とてもお気に入りだったので,ちょっとずつ rm() 関数を入れています。気にしすぎか? 出力はこんな感じ。

HAD2R 多重クロス表
多重クロス表のコードはちゃんと出ますが,あまり実行したくない。こんな感じです。見たい気持ちにならない。まあ,5つも設定する方が悪いんですけどね。しかもこのデータで。

でもって,いちばん最後に,長すぎるからあと残りの75の表は省略したよ,ってメッセージが出ています。ひええ。ということで,どうしても多重クロス表が必要なときは,よく考えてやりましょう。お疲れ様でした。
