(4)補遺：どれくらい偏ると「目立つ」のか

2023年10月12日 15:16

まず2×2表でシミュレーション

とりあえず、一番簡単な2×2クロス表で、シミュレーションをしてみましょう。次のようなシートを作りました。

左上が検定したいクロス表です。総度数や周辺度数を変化させると、クロス表のバリエーションがいくらでも増えるので、それらは固定しておきます。黄色く塗られたセル（PXの位置）の数値を変えると、その他のセルも度数が変わります。右側の「Ex」は期待度数です。総度数と周辺度数を固定していますから、期待度数も固定されます。
その下の「5％臨界値」がカイ二乗分布、自由度１の右側5％点です。
その左側の「カイ二乗値」が、その上のクロス表から計算されたカイ二乗統計量、「p値」は有意確率です。いまは、期待度数と一致していますから、カイ二乗統計量は０、p値は１ですね。では、少し値を変化させてみましょう。

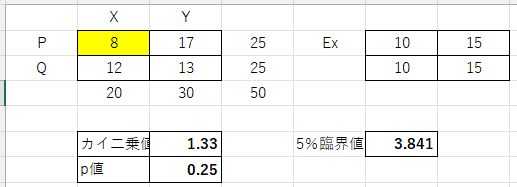
クロス表の左上、PXのセルの値を少しずつ変化させると、カイ二乗統計量が少しずつ大きくなり、p値が少しずつ小さくなっています。3つめの画像で、PXが7になると、カイ二乗統計量は３で、「けっこう大きいけどぎりぎり目立たない（臨界値より小さい）」感じですね。これを6にすると、しっかり目立ちそうです。

はい、その通りになりました。

Rでスクリプトを書いてみよう

同じことを、もうちょっとスマートにできないかと思って、スクリプトを書いてみました。あんまり上手なコードではないのですが。

# ===========================
# クロス表のカイ二乗値シミュレーション
# ===========================

# シミュレーションを記録するデータフレーム
data <- data.frame(x1=0, x2=0, x3=0, x4=0, Chisq=0.000, pVal=0.000)

# サンプルサイズ、行数、列数：しばらく2行2列に固定
n  <- 50
rowsize <- 2
colsize <- 2

# 行、列の周辺度数
rsum <- c(25, 25)
csum <- c(20, 30)

# 自由度に該当するセルの度数からその他のセルの度数を計算する
makeTable <- function(x0) {
  x.tmp <- c(0,0,0,0)
  while (1) {
    x.tmp[1] <- x0
    x.tmp[2] <- csum[1]-x0
    x.tmp[3] <- rsum[1]-x0
    x.tmp[4] <- n-sum(x.tmp[1:3])
    if (x.tmp[4]>=0) break
    else x0 <- x0+1
  } 
  return(x.tmp)
}

# 初期値＝1行目、サンプルサイズの4分の1
i <- 1
x0 <- rsum[1]*csum[1]/n

# ループする
while (x0 >= 0) {
  x <- makeTable(x0)
  res <- chisq.test(matrix(x, nrow=rowsize))
  data[i, 1:4] <- x
  data[i, 5:6] <- c(res$statistic, res$p.value)
  i <- i + 1
  x0 <- x0 - 1
}

data[data$pVal >= 0.001, ]

x0 <- rsum[1]*csum[1]/n
plot(data$x1, data$Chisq, type="l", 
     xlim=c(0,x0), ylim=c(0,25), 
     lty=1, xlab="x1", ylab="Chisq",
     main=paste("2x2Table R(",rsum[1],",",rsum[2],")xC(",csum[1],",",csum[2],")",sep=""))

# 臨界値を示す赤線
y0 <- qchisq(0.95,1)
lines(x=c(-1,(x0+2)),y=c(y0, y0), col="red")
text(0,y0,"Critical Value", col="red", adj=c(0,1))

エクセルでのシミュレーションと同じ総度数、周辺度数の表でためしています。出力されたグラフがこちら。

グラフの「X1」が、最初の画像のPXセル（黄色く塗られたセル）の数値を表しています。X1＝７だと赤い線より下ですが、X1＝６で赤い線を超えて「目立っている」ことがわかりますね。それよりも偏ると、あっという間に目立ちすぎ状態になります。

変化させる列を変えてみたら・・・

では、数値を変化させる列を、X列ではなくY列（2列目）にしてみたらどうでしょう。スクリプトの「行、列の周辺度数」を書き換えることで試すことができます。「csum <- c(30, 20)」に書き換えてみると、こうなります。

X1が12あたりまではギリギリ目立たなくて、11だとアウト、みたいにみえますね。実際に数値を計算してみると、12だとカイ二乗統計量は３で「目立たず」、11だとカイ二乗統計量は5.33で「目立つ」、ということでした。

しかし、これはすでに分かっていたことです。
なぜって？
この記事の最初の方に貼り付けてあるエクセルシート画像をよく見てください。ちょうど4枚目の画像で、右下が11になっていて、カイ二乗統計量が5.33です。そうです。クロス表はセルの配置を上下左右入れ替えても、計算される統計量は変わりません。足し算の順番が変わるだけですからね。

2×3だと一気に複雑に

じゃあ、もう少し自由度の高い表でもやってみよう！　と、思うだけは思ったのですが、2×3になっただけで、もうお腹いっぱいな感じでした。何しろ、変化させるセルが2カ所になるぶん、グラフも複雑に。興味のある方はご自分でシミュレーションしてみてくださいね。

使いたい方は自己責任で、ご自由に

シミュレーション用エクセルシート

シミュレーション用Rスクリプト