HADを使ってみた：5.度数分布表と正規性の検定

度数分布表も，統計の授業の最初の方でかならず登場しますね。小学校の算数でも，度数分布表，ヒストグラムくらいまでは学習しますから，基本中の基本と言ったところでしょう。HADでこの2つの分析をすると，なんとなく同じようなものが出力されるなあ，と思うのですが，よく見ると重要な違いが。そのあたりに注意しつつ，まとめてみましょう。

カテゴリ変数の場合

HADでは，水準数が15までをカテゴリ変数であると認識する設定になっているようです。これは，【HADの設定⇒分析設定】で確かめることができる。けれど，この数を調整すると，実際，何がどうなるのかを実感した経験は今のところありません。そのうち経験したら書くことにしましょう。おそらく，ｔ検定や分散分析の独立変数に設定されたときに，水準数がいくつであるかが影響するのではないかと思います。
また，すぐ下に「独立性の検定で連続性補正を行う」のオプションがありますが，独立性の検定はクロス表のところに関係するので，ひとまずスルーです。

さて，カテゴリ変数に対する度数分布表は，たとえば以下のようになります。要約統計量のところで書いたように，あえて１つだけ欠損値にしています。度数分布表の見た目がちょっと（？）な感じですが，Excelのグラフなので，縦軸の設定など，Excelの機能の範囲で好みの様式に変更すればよし。（note では，図をクリックすると大きく表示されるはずです！）

統計量として，平均値，標準偏差，歪度，尖度のほかに「正規性」の検定結果が出ています。ヒストグラムのところでみたように，これは，コルモゴロフ・スミルノフ検定の結果（リリフォース補正あり）です。プロットのさらに右側に，一様性の検定結果が出力されます。一様性の検定とは，

等比率に対する適合度検定（χ2乗検定）を行います。（https://norimune.net/640）

つまり，どのセルも同じ確率をもっているかどうか，ということですね。上記の場合はp値が .993 で「等比率である」という帰無仮説は棄却できません。つまり，各セルの数値に差があるけど，統計的に意味のある差ではないよね，ということでしょう。まあ，この場合はほとんど自明のことなんですけどね。

では，ヒストグラムと比較してみましょう。ヒストグラムを出すと上のようになりますよ。はい。ほとんど同じですね。ヒストグラムの方には，一様性の検定は出てきません。確率，有効確率も出てきません。なので，カテゴリ変数については，ヒストグラムを使っても，とくに問題はおきない。けれど，注目したいカテゴリの確率または有効確率に興味のある場合が多いでしょうから，素直に度数分布表を選んだ方がいいでしょう。

連続変数の場合

さて，連続変数の場合はどうなるか。ヒストグラムとの比較で，その違いが分かりやすいのは花弁長（Petal.L）でした。まず度数分布表の結果です。

長いので途中で切っていますが，タイトル行，欠損値，合計まで含めて46行のながーい表です。ですから，グラフと統計量の下，次のグラフまでは30行ほど空白があります。

もう一つ注意するべきことは，出現値がとんでいるところの処理です。１から1.9までは0.1ごとに増えていますが，そこから急に３にとんでいますね。2から2.9までの数値は表れない，ということですね。それが，グラフではどのように表現されているかというと，1.9のとなりに3が来ていることからわかるように，2～2.9の値が出現しないことは，数値をよく見る以外に見つける方法がありません。度数分布表ですから，出現値と出現回数を単純に棒グラフにするこの描き方で間違っていません。しかし，このグラフをヒストグラムだと思って解釈するのは間違いですね。棒と棒の間隔があいていないので，見た目だけは完全にヒストグラムなので要注意。連続変数で度数分布表を出力するのは間違いのもと。ここ重要。

このことはヒストグラムの出力（上に示した）と比較するとよくわかります。ヒストグラムで作成された表には，度数０の部分がちゃんとあり，ヒストグラムの棒の長さが０になっている部分がある。連続変数の分布の表現としては，これが正しい。つまり，「このへんの数値（この場合は2から2.9まで）はデータに出現していませんよ」というのも，連続変数としては重要な情報なんですから。

ヒストグラムで，こんなふうに山が複数になる（多峰性の分布といいますね）ときには，別の何かの要因が異なっている，つまり複数の種類のデータが混じっていると考えなさい，というのが統計処理の基本でした。この場合はもちろん，種（Species）によって値が異なり，実際には3種類のデータが混在しています。しかも，2～2.9が空白になっている＝値が重なり合っていないので，ものすごく値が異なる種が混じっていることがわかります。
※余談ですが，放送大学科目「身近な統計」では，松坂やダルビッシュの，球速のデータをヒストグラムにして，データが多峰性を示すのは，球種によって球速の分布が違うからだ，という説明をしていました。たいへん面白いデータでしたね。

ヒストグラムの上に「出現値43」と出ています。花弁長のデータは，43種類の異なる値があるよという意味ですね。これは明らかにカテゴリ変数の基準となる水準数を超えているので，このようなデータを指定して「度数分布表」分析をしたときには，

この変数は水準数が設定範囲を超えていますので，分析を中止します。

としてしまうか，あるいは，

この変数は水準数が設定範囲を超えていますが，このまま出力しますか。（水準数によってはかなり時間がかかります）　続行する／中止する

などとして，ユーザに選択をさてもよいのではないか，と思います。

ところで，さっきのヒストグラムに変なところが１つあったのに気付いたでしょうか。今回出力してみてびっくりしたのですが，見た目が度数分布表に近い，級数の多いヒストグラムで比較してみようと思って，級数を20に指定したのですね。前回もやったんですが，そのときは変数1つでした。今回は変数５つとも投入したら，なんと。ヒストグラム作成のための表が，下の変数とかぶってしまいました。ということは，級数20などという設定をする奴はいないだろう，という前提で出力シートの設計がされているのでしょうか？　これは大変。上に表示した部分のすぐ下を見ると明白です。

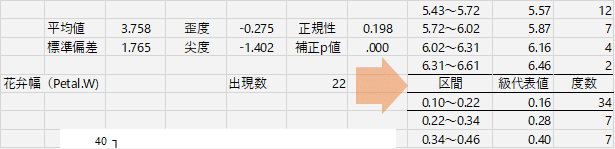
ほら，大変でしょう？　花弁長の最大値は 6.9 ですから，区間 6.31～6.61で表が終わってしまっては困ります。ということで，

ヒストグラムの水準数の上限は15です。

と制限を設けるか，水準数に応じて出力位置をずらすようにするか，が必要ですね。ちなみに，スタージェスの公式を使って計算したときに，ヒストグラムの級数が15になるためには，15000 以上の N が必要らしいので，15を上限としても大きな問題はないように思います。20などという数字を入れて遊ぶのはわたしくらいのものでしょう。すいませんでした。

注意しましょう

ということで，整理します。度数分布表とヒストグラムは，出力される情報がよく似ていますが，
１．カテゴリ変数の場合は，度数分布表を選びます。
　　ただし，ヒストグラムを用いても，実質的な問題は生じません。
２．連続変数の場合は，ヒストグラムを選びます。
　　ただし，出現値ごとの確率や累積確率などに興味のある時は，度数分布表が有効です。
３．ヒストグラムの級数を自分で指定するときには，せいぜい15にしておきましょう。どうしても20以上の級数がほしいときは，1変数ずつ分析しましょう。

HAD2R：度数分布表

度数分布表で出力されるコードは，こんな感じですね。

table(dat$Species)
table(dat$Petal.W)

このコードを実行すると，実に味気ない結果を出力してくれます。

もうちょっと何とかしようと思ってみますが，

d <-data.frame(x <- table(dat$Petal.L))
colnames(d) <- c("出現値","度数")
barplot(x)
d

まあ，これが限度でしょう。上に書いたように，このグラフをヒストグラムと解釈してはだめです。途中でX軸の値がとんでいるからです。
そういえば，一様性の検定については，HAD2Rではコードが出されません。一応出しておきましょう。

chisq.test(table(dat$Species))
chisq.test(table(dat$Sepal.L))

などとします。簡単なコードだし，カイ二乗検定はけっこうよく使うので，ここでコードを出しておいてもいいんじゃないかと思います。

HAD2R：正規性の検定

最後に，正規性の検定ですね。正規性という名前なんですが，データの分布と理論分布とを比較する検定のようで，ここでは正規分布と比較しているようです。HADの出力はこんな感じで，

HAD2Rはこんなのが出力されます。（長いので途中で改行しました）コードの途中にある "pnorm" というのが，正規分布を指定する引数です。

ks.test(na.omit(dat$Species), "pnorm", 
    mean=mean(dat$Species, na.rm=T), 
    sd = sqrt(var(dat$Species, na.rm=T)))
ks.test(na.omit(dat$Sepal.L), "pnorm", 
    mean=mean(dat$Sepal.L, na.rm=T), 
    sd = sqrt(var(dat$Sepal.L, na.rm=T)))

ks.test は，コルモゴロフ・スミルノフ検定をする関数です。Rでこのまま実行すると，警告が表示されます。

タイ，つまり同じ値が複数出てくるよ，という警告なんですが，データは勝手にいじれませんから，出てくるものは仕方がない。出力される統計量とp値は，HADのものと完全に一致しています。（というか，HADの正規性の検定のコードを書くときに，ks.test が参考にされているので当然なのですけど。）ただし，リリフォースの補正というのが，よくわかりませんでした。これは宿題ですね。p値が小さくなっているので，より厳しい検定をするような補正だと考えられます。SPSSのアルゴリズムを書いた文書は手に入れていて，リリフォースの補正についても書いてあって，読もうと思えば読めるんでしょうが，英語＋数式という２つの難関（とくに後者）がありまして，はい。

正規性の検定は，ほかにも種類があって，ジャック・ベラ検定は別のライブラリ導入が必要，標準ライブラリで実行できるものには，Shaprio-Wilk 検定があるようです。が。どの検定がどうで，みたいな話は，わたしには無理です。ということで，今回は以上なり。