
HADを使ってみた...んだけど:一要因分散分析
何だか中途半端なタイトルにしてしまったのは,もやもやが残ったまま書いているからなんだが,とりあえず分散分析について調べたり考えたりしたことをまとめよう。HADの分散分析出力はこれでもかというくらいに丁寧だ。
分散分析って難しい
分散分析は難しい。何が難しいかって,説明するのも難しいのだけれど,統計法の教科書で分散分析のところを読んでいて,どうして二乗和がふたつに「分解」できるのか,訳が分からなかったことは記憶している。そのあといろいろな本を読んでいて,三平方の定理では,2つの二乗和の合計がもう1つの二乗になるし,だからその2つの辺は直行しているわけで,二乗和が最小になるということは,そういう関係を見つけていることなのか,最小二乗法と言うのはそういうことをしているのか,などと少しずつつながりだしてから面白くなってきたのだが,よし説明してみろと言われると,まだできない。
などという与太話はさておいて,HADの分散分析の出力は細かい。通常の統計法の教科書には,いわゆる「分散分析表」が出てきてほとんど終わるのだが,HADは違う。そこがまた,ちゃんと理解しようとするとハードルの高い所でもある。結論から言うと全部理解できていないのだけれど,とりあえず考えたことだけは書いておかないと忘れてしまうので,間違いや思い違いが含まれているかもしれないことを承知の上で,まとめておこう。
エクセルで一要因分散分析
HADには,「分散分析」という文字がぱっと見えない,という不思議な特徴がある。J5セルあたりにある「回帰分析」というオプションを選択すると,画面ががらりと変わって,かなり複雑な分散分析や回帰分析ができるようになるのだが,私は通常の一要因分析でアップアップしているので,ここには立ち入らない。
その一要因分散分析は,【分析】メニューの「平均値の差の検定」で行うことができる。初歩的な一要因分散分析の材料として,今回は,『データ解析テクニカルブック』(森 & 吉田, 1990)の例題3.1.1(p.86-87)を用いることにした。まず,データと,エクセルによる分散分析の結果を出しておこう。まわりくどいのだが,通常「分散分析表」といったらこの程度のものだということを示しておくと,HADの出力との違いが鮮明になる。
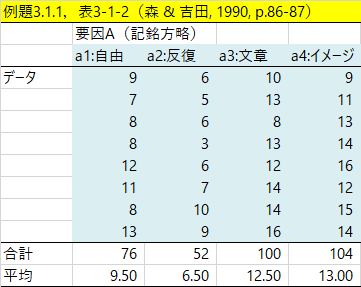
エクセルの「データ分析」ツールでは,ツールのメニューから「一元配置分散分析」を選び,データ部分(上図で薄い水色の部分)を範囲として指定し,OKすると分析ができる。下の図その出力だが,統計法の教科書によくのっている分散分析表はこれである。「変動」ではなく「平方和」,「観測された分散比」ではなく「F値」などとしている教科書が多いだろうが,数値の並び順などは同じである。
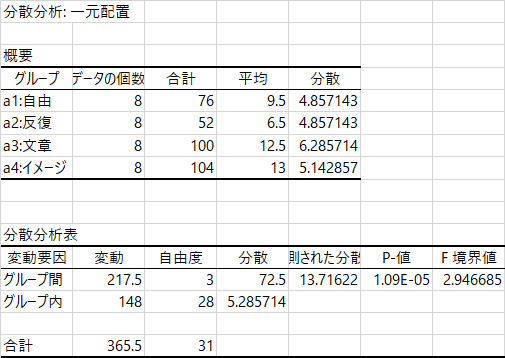
ところでまったくの余談なのだが,エクセルの「データ分析」ツールの,ある種の「分かりやすさ」というか「(素人的な)とっつきやすさ」は,このような(つまり上に示したような)「表の形式」でデータを入力すれば分析できてしまうところにあるかもしれない。が,これに慣れてしまうと(かつての私のように),RやHADなどで分析するときにどうやってデータを入力すればよいのかわからなくなってしまう。たとえば,上述のデータだと,この表のとおりに入力しても,同じ結果は得られない。なぜなら,
このデータは対応のないデータであり,「32人分のデータ」である。したがって,RやHADで分析させようと思ったら,「32行」のデータを作らなければならない。
つまり,こんなふうに。
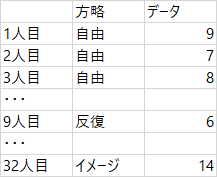
ずいぶんはしょって画像を作っているけれど,言いたいことは伝わるだろうか。さっきの表(一番最初に出した画像)を,こういう風に変換させることができないと,エクセルからHADやRに乗り換えられない。わかってしまえば何と言うことはないのだが,高いハードルに感じる人はいると思う。
なんだそんなこと,と思われるだろうか。笑うなら笑っていただきたいが,私はこの書き換えが最初わからず,RやHADがうまく使えなかった。分析ソフトに与えるデータというのは,1行が1人分である。わかってみれば単純なことだが,どちらかというとエクセルが親切すぎるのである。
HADで一要因分散分析
では,そうやって書き換えたデータを用いて,HADで分析してみよう。同じ結果になるに決まっているのだが,出力がかなり違うので,それを見比べたいのである。手順は次の通り。データを入力したときに,方略を「Plan」,データを「Score」という名前にしてある。
使用変数として,Score(従属変数),Plan(独立変数) を設定する
⇒【分析】
⇒「平均値の差の検定」
⇒オプションは「対応なし」(デフォルト)のまま
分析手順がt検定とまったく同じになるところが,HADの特徴。もう書いたっけ。結果はこちら。
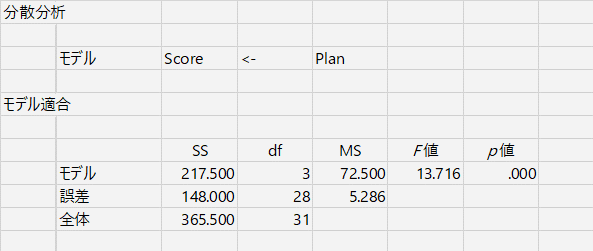
まず私が見慣れなかったのが「モデル」という表現であった。ここに書かれているのは,
Score ← Plan
という「モデル」で,まあ解釈するとすれば,「Plan」という変数を使って「Score」を解釈してみたよ,という感じだろうか。「Score」ってさあ,「Plan」によって決まる部分があるよね,という感じでもいいかな。ほら,「Plan」が違うと,「Score」が違うでしょ。という感じ。ほんとだ,じゃあこの「Plan」を,わたしもやってみようかなあ,と,実際の勉強法なんかの研究では,そういうふうに影響力を持ってくる。もちろん,「Score」の違いは,その人が勉強を好きかどうかとか,得意な科目かとか,はたまた,その日の体調とか,出題範囲の山勘があたったかどうかとか,教えてくれる先生の好き嫌いとか,テストのときの椅子の固さとか,そういう,一見しょーもないことも影響したりするのだけれど,だからといって,ぜーんぶの影響を考えることなんかできるはずがない。そこで,影響しそうなこと,できればよい影響がありそうなことを試してみて(この場合は記銘方略),その他のことはできるだけ公平にしておくと,それが実際に影響しているのか(方略が記憶に効果があるのか)がわかる。ざっくりこんな感じで,心理学の実験は行われている。で,「影響ありそうなこと」として何をもってきたの? 何に影響すると考えて実験しているの? というのを整理したのが「モデル」ということでしょう。あってるかなあ? 違ってはいないと思う。
で,話を戻すと,ここでは「記憶方略」が勉強に影響すると思うよ,だから,記憶の実験して,その「成績」をデータにして分析してみることにするね,という「モデル」を作ったということでしょう。
その下にある「モデル適合」のところに,一般的な分散分析表(に近いもの)が出力される。(に近い)などと注釈をつけたのは,これが二要因以上になると表の形が変わるからなんだが,そこには今は触れない。
平方和(Sum of Square),df(自由度:Degree of Freedom),平均平方和(Mean of Square)などと英語の用語を多少知っておくと,海外の論文でも分析結果だけは読めたりする。
またまたどうでもいい話だが,HADには英語バージョンもある。バージョンが違うのではなく,表示言語を英語と中国語に切り換えることができる。【HADの設定】から切り換えられるので,気になる向きは試されるとよい。賢くなった気分になるかもしれない。
以上が,HADの分散分析結果出力のもっとも基本的な部分である。そして,これで終わらないのがHADである。
Welchの分散分析
分散分析表の下に,R2乗とかAICとかの適合指標の表と,要因の効果という表があるのだが,そこに「Welch検定」(!)なるものが登場する。

Welch検定はt検定で等分散を仮定しない場合に登場する名前だが,これが3水準以上の分析にも拡張できるというのである。たぶんHADを使っていなかったらずっと知らずにいたでしょうなあ,と思ってしまう。この分析については,青木先生のサイトにF値を算出する数式が示されている。
けっこう難儀な数式なのだが,この通りエクセルで計算すると,なるほどHADの結果と同じ数値が(当たり前だが)。そして,この検定は,Rでは oneway.test という関数で実行できるらしい。残念ながら平方和の情報までは出てこないのだが,検定はできる。そして,やはり青木先生のサイトによれば,一要因分散分析でも,常にこのWelchの検定(つまりは oneway.test)を使えば間違いない,というシミュレーションが示されている。
ちなみに,Rでよく使われる分散分析の関数 aov は Welchの方法を使っていないし,もちろん(?)Excelのデータ分析もWelchではない。Welchで間違いないなら,分析ツールのデフォルトをWelchにしてほしい。なに? だったらHADを使えばいい? その通りなのだが。
あと,書き忘れたのだが,平方和の計算がHADでは「タイプ3」になっている。タイプが違うと何が違うのかは難しいので書かないが,タイプ1だと(つまりRの aov 関数だと),2要因以上になったときに,要因を指定する順序によって平方和が違ってきたりする。これはRで試したから確か。そういうのは困るので,タイプ2や3を使うとよいぞ,と参考書などに書いてあった。でも今は1要因なので,スルーしよう。影響はないはずである。
多重比較
というわけで残るは多重比較なのだが,これがまた悩ましい話題である。どの方法がどう,という説明は専門家に任せることにして,HADが現在デフォルトで採用しているのは Holm の方法である。ほかに「修正Shaffer」「Shaffer」「Bonferroni」も選択できるので,こだわりがあるなら,【HADの設定】⇒【分析設定】で変更ができる。ただし,Rでよく使用される Tukey の選択肢はない。(HAD2Rでは Tukey の関数を出しているのに!)
ところで,HADの多重比較の出力はまことに丁寧である。まず全体平均についての表と検定があり(「切片」と表示されているのがそれ),次に水準ごとの平均値についての表と検定があり,それから水準の組についての平均値差と検定の表がある。

このように,水準ごとの平均値を計算してくれるというのはたいへんありがたい。実は修士論文のためのデータ分析をしている途中で,水準ごとの平均値と標準偏差を一覧表にして出力させる関数をRで作り,それを分散分析や多重比較の関数とセットにして走らせていた。使う変数や条件を指定すれば一気に結果が出てくるのでたいへん重宝したが,HADではさらに丁寧に結果を示してくれる。痒い所がなくなってありがたい。
なので,同じような表をRでも,と思って挑戦してはいるのだが,まだ途中である。
ところでこれは何の検定?
ところで,たとえば各水準の平均値が出てくるのはいいのだけれど,これに対して1つずつt検定の結果が示されている。これはいったい何を検定しているのか。2つの平均値を比較しているわけではないので,考えられるのは理論値との差の検定(1標本のt検定)である。ならばと考えて,変数を中心化して(つまり平均を0にして)同じ分析をしてみたところ,平均値が0に近い水準でp値が高くなった。t検定の式に当てはめてみるとやはり結果が一致した。
つまりこれは,分析前に結果が「中心化」あるいは「標準化」されていることを前提にした出力だと考えていいだろう。そうでないなら,平均=0という帰無仮説を設定する意味がない。ここで有意になるということは,この水準の平均値は,全体平均とは差があると考えてよい。
また,中心化してから分析すると,プロットも0点を基準に描いてくれるので,より水準間の差が見えやすくなる。この条件だと全体平均より低いとか,この条件なら全体平均より高いとか,要するに議論がわかりやすくなるわけだ。
ということで,多重比較の部分だけ,中心化しない分析と,中心化した分析とを見比べておきましょう。下に出したのは中心化した従属変数を用いた分析。モデルは同じ。多重比較の表はまったく同じ数値が並んでいるのだけど,水準ごとの平均値とプロットはずいぶん違って見える。結果のアピールにどちらが効果的かをよく考えて使い分けるのが良いと思われる。

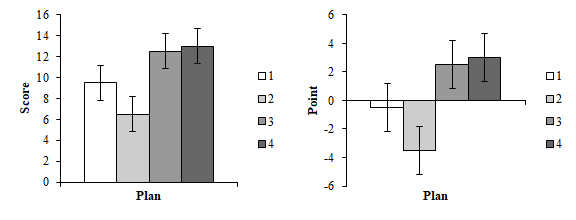
HAD2R:分散分析
分散分析でHAD2Rが出してくれるコードは,次の通りです。実行結果といっしょに乗せておきましょう。
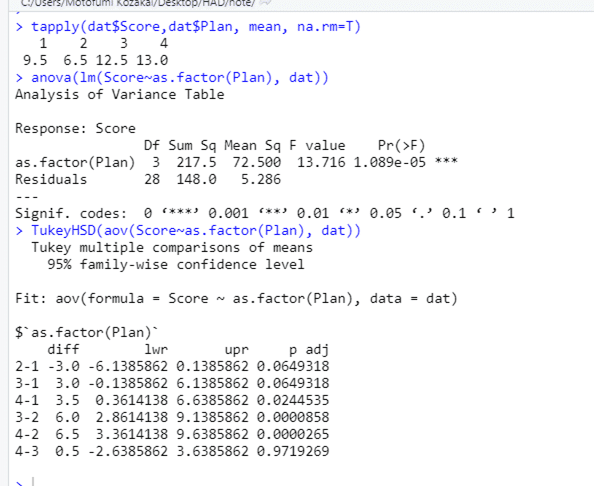
tapply 関数が入れてあるのは,やはり水準ごとの平均値はどうしてもほしいからでしょうか。しかし何といっても,多重比較の結果の違いは歴然。調整p値の値もけっこう違っていて,1と2のペア,3と1のペアでは,Holm だとぎりぎりで有意, Tukey だとぎりぎりで非有意,という何とも悩ましい結果になっている。95%信頼区間の幅も,符号が逆になっているので見づらいのだけれど,Tukey のほうがだいぶ広くなっている。
Rでは pairwise.t.test という関数で,p値の修正方法を指定して一要因の多重比較ができるらしい。やってみると,出力はそっけないのだけれど,HADと同じ修正p値が得られる。せっかく標準ライブラリで使える関数なので,HAD2Rも,こっちに入れ替えてもらってもいいかな,と思う。が。平均値の差とか,信頼区間とか出力されないのが難点。悩ましいねえ。
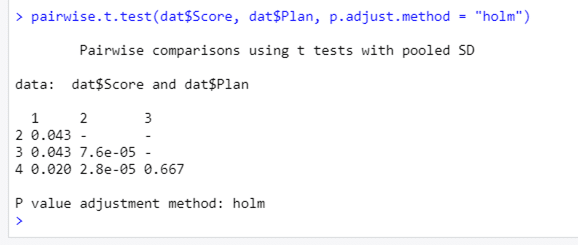
というわけで,そんな悩ましさを解決するべく,いつものように,「HADみたいにRしたい」プロジェクト(いつからプロジェクトになったんだか…)を実行中なのだが,何せ出力するべき情報量が多くて難儀している。ずいぶん長くなってしまったんで,また次の機会と言うことに。
