
HADを使ってみた:4.ヒストグラムとカーネル密度
ヒストグラムを描いてみる
ヒストグラムは,データのばらつきを視覚的にとらえるための基本的な方法の一つですね。さっそくやってみます。前回までと同じように iris のデータを使います。
手順は簡単で,ヒストグラムを作成したい変数を並べ,【分析】⇒「ヒストグラム」を選択して,ついでに,ヒストグラムのオプション的な扱いになっている「カーネル密度」にもチェックを入れてOK。こんな感じに出力されます。

細かいことなんですが,プロットの上には「がく長(Sepal.L)」と出力されているので,ラベルは有効になっているようです。しかし,プロットのX軸の名前には反映されていません。うーむ。これは修正をお願いしたほうがよいのかな?
カーネル密度とは,清水先生のブログ記事によれば,
ヒストグラムは階級数の設定によって形がかわります。そこで,階級数に依存しないようになめらかなヒストグラムを書きたい,と思った場合に使えるのがカーネル密度です。これは,ヒストグラムをわざとぼやかして,滑らかにする方法です。
だそうです。階級数に依存する,なんてところは,いかにも統計学の試験に出そうな感じがしますね。「ヒストグラムをわざとぼやかして」なかなか味わいのある表現ですね。ヒストグラムの形にスポンジケーキを立てて,上から生クリームをたっぷりかけたら,カーネル密度のようになりそう。(どんな比喩なんだか…)
だから,これ,ヒストグラムとカーネル密度推定と2つ重ねると,ヒストグラムの情報をカーネル密度推定が補ってくれて楽しそうですね。残念ながらそういう機能はHADには実装されていない。あとでRでやってみよう。
ところで,HADのヒストグラムには2つのオプションがあります。級数の指定と,正規分布曲線の表示です。こっちを先に試してみましょう。
級数を変える
グラフ設定(【分析】⇒グラフ設定)をみると,左上にヒストグラムの設定があります。ここで「ヒストグラムの級数」がまず設定できます。デフォルトは12。つまり,ヒストグラムの棒が12本立つわけだ。これをもう少し細かくしたいなら,数を増やす。もっと大雑把でいいなら数を減らす。こんな風に(級数は左が20,右が5)。同じデータなのにずいぶん違う。

「標本サイズによって変える」にチェックすると,設定した数値ではなく,標本サイズをもとにHADが計算した級数で描画される。設定は20のままここにチェックすると,最初に出したのと同じになります。級数は8。
なぜ8になるのかは,おそらく,Sturgesの公式なんかによるものと予想します(HADのVBAソースを見ればわかるんですが,そこまでの根気はない)。この公式は,サンプルサイズに対して対数(底=2)をとり,それに1を加えた数を級数にする,というもので,1926年に発表されたものらしい(http://cse.naro.affrc.go.jp/takezawa/r-tips/r/61.html による)。
ほかにも計算方法はあるらしく,Rのヘルプによると,級数を設定する breaks オプションのデフォルト設定は"Sturges"で,ほかに"Scott"と"FD"が指定できると書いてあるのだが,ヒストグラムを描く変数によっても変わるので,「実際に級数がいくつになるかは,やってみないと分からない」ことだけは確かなようだ。なので,自分好みにしたいときは breaks = c(5,6,7,8) とかで数値を設定するのが確実でしょうね。
正規曲線を表示
さきほどの級数設定の下に「正規曲線を表示」というオプションがあるのでチェックしてみると,こんな感じのが出力されます。グラフの下に算出されている平均値と標準偏差を用いて正規分布曲線を描くとこんな感じ,というグラフだと思われます(HADのVBAソースを見ればわかるんですが…)。
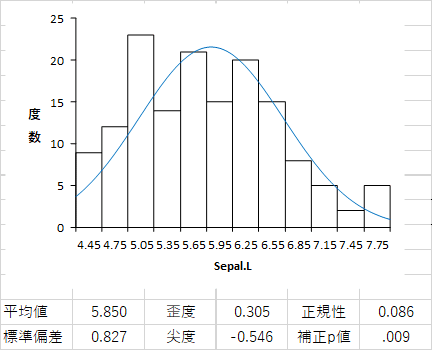
この曲線が,ヒストグラムの形状とだいたい一致していれば,そのデータは正規分布に近いなあとわかるし,そうでないならそうではない。もっとも,データが正規分布に近いかどうかは,「正規性」としてすでに統計量が算出され,p値も出されているので,それを見たほうが手っ取り早いぞ,とも思える。ただし視覚的な判断は数値による判断とはやはり別物と言う感じがするので,正規曲線を重ねるのは面白いと思う。
ここに出ている「正規性」は,コルモゴロフ・スミルノフ検定の結果である(清水先生のブログ記事を参照)。Webで検索すると,この検定の「帰無仮説 (H0) は標本分布が正規分布に従うこと」だと書かれているので,上の図のp値が.009ということはそれを棄却している,つまり「正規分布とはいえない」ということになる。
ヒストグラムの区切りを指定したい
HADでヒストグラムを描いていてちょっと残念なのは,自分で級の区切りを指定できないことです。きりのいい数で区切りたいときに,ひと手間かかる。といっても,そういう機会がそれほどあるわけではなく,たとえば回答者の年齢なんかをヒストグラムで,30代,40代,50代,とか出したいなあ,くらいだろうか。そういうときは,=int(年齢/10) などの式でもう一つ変数を作り,そっちの変数でヒストグラムなり度数分布表なり作るのがよい。で,「1=30代, 2=40代」のように値ラベルを設定しておけばOK。
HAD2Rを試してみよう
出てくるコードはどちらも簡単で,まずヒストグラムは,
hist(dat$Sepal.L)
とかで,カーネル密度の方は,
plot(density(dat$Sepal.L))
とか。
ヒストグラムを自分好みにする
まずヒストグラム。でも単に hist() 関数を使うだけだと,級数を自分の好きな数に設定できない。自分で区切りを指定したいときは,breaks = c(20,30,40,50)のように区切りを並べていくと設定できるのだけれど,扱う変数がどんな数値をとるか見てからでないと設定できない。それから,breaks = 12,と単に数値を指定して「12本でヒストグラム描いてね」と,人間側は思うのだが,出力はそこまで思い通りにはならない。
そこで,ちょっと手を加えて,関数にまとめてみた。
my_hist <- function(x, classnum) {
cp <- seq(min(x), max(x), length.out=classnum)
hist(x, breaks=cp)
}
my_hist(dat$Sepal.L)
my_hist(dat$Sepal.W)
my_hist(dat$Petal.L)
my_hist(dat$Petal.W)cpは,渡されたデータの最小値から最大値までを指定した数(classnumで指定)に分けて,ヒストグラムの棒をどこで切るか指定するための変数。これを length.out に指定すると,棒の数がおおむね指定した通りになりますね。
カーネル密度を重ねてみる
カーネル密度のさっきのコードは,単独で実行するとこんなのを出してくれる。
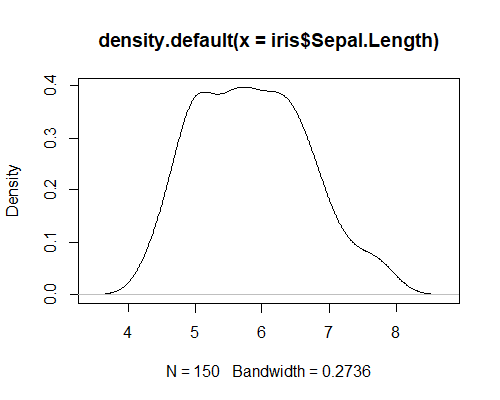
ネット上の記事で勉強したところ,これは lines 関数(つまり,低水準関数ですね)を使うと簡単に重ね書きできるそうなので,ヒストグラムに重ねてみようではないか。おりゃ。
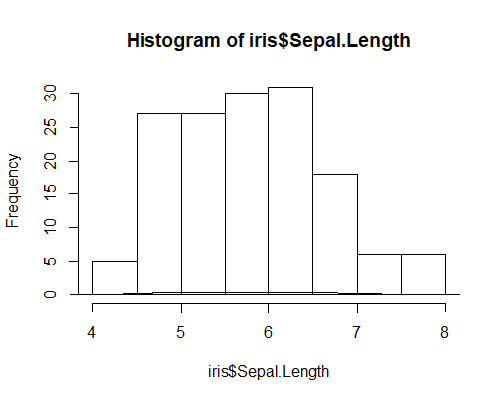
何も変わってない!と思ったらX軸が部分的に2本になったかのような微妙な変化が。残念。とても残念な図になるのは,ヒストグラムが度数なのに対して,カーネル密度が確率なので,Y軸目盛のまったく違う部分が使われているからのようだ,ということに,試行錯誤の末に気づいたので,少々残念だけれどヒストグラムの方のY軸を「確率表示」にしてみましょう。コードはこんな感じ。級数を15に設定して。とりゃ。
my_hist <- function(x, classnum) {
cp <- seq(min(x), max(x), length.out=classnum)
hist(x, breaks=cp, freq=FALSE)
lines(density(x), col="blue")
}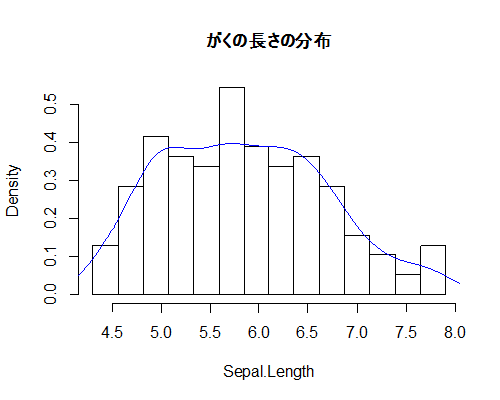
おお,できるじゃないの,Rくん。楽しいぞ。ここまで来たなら,右側にもう1本Y軸を描いて,そっちだけ確率にして,カーネル密度は右側のY軸で描く,ということもできそうなんだけどな。どうやってやるのだろう。Excelだと「第2軸」って設定するんだけどな。これは宿題と言うことで。
正規曲線も重ねてみる
カーネル密度推定の曲線が重ねられるなら,同じ要領で正規曲線も重ねられるだろう,ということで,与えられた変数の平均値と標準偏差を計算して正規分布曲線を重ねるように(例によってあれこれ失敗しながら),関数を書き換えてみた。どうだ。どうでもいいような設定もあるけど。
my_hist <- function(x, classnum, main = "Histogram of x", xlab="x", dc=TRUE, nc=TRUE) {
cp <- seq(min(x), max(x), length.out=classnum)
hist(x, breaks=cp, freq=FALSE, main = main, xlab = xlab)
n <- seq(min(x)-1,max(x)+1,0.01)
if (dc) lines(density(x), col="blue")
if (nc) lines(n, dnorm(n, mean=mean(x, na.rm=T), sd=sqrt(var(x, na.rm=T))), col="red")
legend("topright", legend = c("Density","Norm"), col=c("blue", "red"), lty=1)
}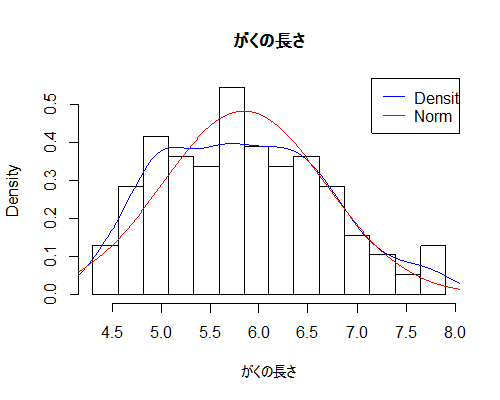
おお。楽しい。青い線がカーネル密度推定で,赤い線が正規曲線ね。こうやって重ねてみると,平均値付近がやや平らになっていて(だから尖度が負の数になっている),そのぶん,平均値よりやや小さい値が多く出ている=つまり山の頂上が左に寄っている=正方向に裾を引いている,ように見える(だから歪度が正の値)。HADでは現状,青い線は重ねられないので,両方出力して,カーネル密度グラフの背景を透明にしつつ,重ねて楽しみましょう。
正規性の検定が出てきたので,コルモゴロフ・スミルノフ検定についてもちょっと調べたのだけれど,それは分析メニューが別にあるので,次回に回すことにしよう。
