
HADを使ってみた:3.箱ひげ図…
箱ひげ図を描いてみよう
HAD箱ひげ図を描いてみます。清水先生のブログによれば,
箱ひげ図というのは、中央値を中心として、上位25%と下位25%の範囲を箱で表示し、最小値と最大値をひげ(?)で表示するグラフです。データの範囲と偏り、分布の仕方などを複数の変数で比較できるのがポイントです。外れ値がある変数なんかがわかります。
とあります。ちなみに上記のブログ記事は開発当初のもの。現在はかなり進化していて,その後の記事では,
これまで負数がデータに含まれていると表示できませんでしたが,それも表示できるようにしました。箱ひげ図では,今流行り(?)のバイオリンプロットを表示できるようにしました。バイオリンプロットとは,箱ひげ図にヒストグラム(実際はカーネル密度)を同時に表示するものです。あと,平均値に印をつけられるようになりました。
となっています。すごい(拍手)。
では,前回までと同じデータ(iris)で,箱ひげ図を描いてみましょう。箱ひげ図を描きたい変数をいくつでもいいので設定して,【分析】⇒箱ひげ図⇒OK で完了。こんな感じになります。

となりにあるのは,HAD2Rで出力されたコードを実行して描いたプロットをはりつけたもの。HADではもう少し大きめに出力されるのですが,同じだぞ,ということを強調するために,Y軸の最大値を9から8に,目盛間隔を1から2に変更し,さらに縦横のサイズを変更して,見た目をできるだけ似せてあります。
ちなみにHAD2Rで出力されるコードはこちら。まあ,簡単なので書くまでもないのですが,右のプロットはこれで出したものです。
dat <- read.csv(" .../csvdata.csv")
subdat <- subset(dat, select = c(Sepal.L,Sepal.W,Petal.L,Petal.W))
boxplot(subdat)さて,プロットを2つ見比べて,全く同じ…ではない。
Rのほうは中央値の線が太いとか,ひげが破線だとか,そういう見た目ではなく,違うのは「がく幅 Sepel.W」(Rのプロットを小さくし過ぎたので文字が消えている! ごめんなさい)のひげの上下にある小さな〇で,これは「外れ値」です。しかし,HADで出力された箱ひげ図には,外れ値はプロットされていません。これはたぶん,プロットの描画方法の違いも関係してきます。ちょっと面倒そうです。
箱ひげ図という棒グラフ?
「エクセル 箱ひげ図」でWeb検索すると,こんなページが見つかります。
ちょっと待て。箱ひげ図は決して「棒グラフ」ではない。なのになぜ「棒グラフ編」? 記事を読むとわかりますが,エクセルに箱ひげ図の機能が搭載されたのはわりと近年のことで,わたしが放送大学で履修した「身近な統計」('12)でも,棒グラフを使って箱ひげ図を描く方法を,講師の渡辺美智子先生が解説しておられました。ずいぶん面倒なことをしなければ箱ひげ図が描けないものだと思ったのを覚えています。HADで出力された箱ひげ図をクリックして,「グラフのデザイン」タブの「グラフスタイル」を変更すると,このグラフが3つの棒グラフの積み重ねであることがわかります。
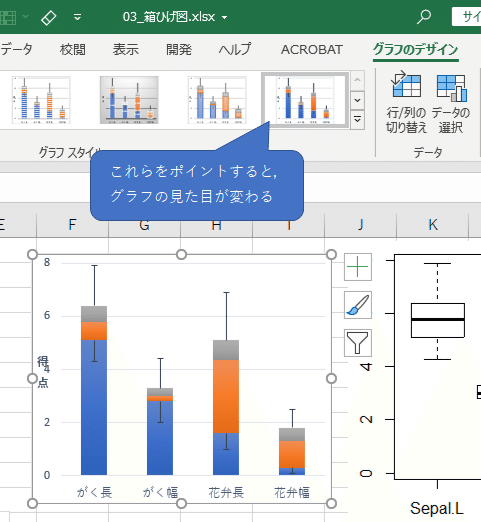
その後,エクセルの統計グラフにも「箱ひげ図」が追加されて,ローデータから直接描けるようになりました。そうすると,外れ値も描けます。こんな感じ。
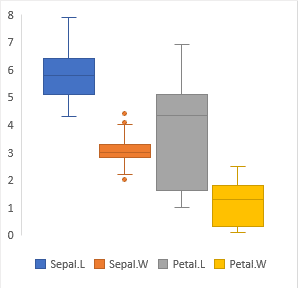
ならばHADも,この機能を使うべきではないのか? なぜ棒グラフを使うのか? と疑問符をならべたくなりますが。ことはそれほど単純ではなく。
統計量で描くか,ローデータで描くか
2つの箱ひげ図,つまり,積み上げ棒グラフの箱ひげ図と,統計グラフの箱ひげ図の最大の違いは,それが統計量をもとに描かれたものか,ローデータをもとに描かれたものか,であると思います。
HADが採用しているのは,前者,つまり「統計量」による「積み上げ棒グラフ」方式です。四分位数や四分領域(四分位偏差=四分位範囲÷2のことと思われます)が表示されている右側に,もう一つ別の表があり,そこには「Q1,Q2-Q1,Q3-Q2,…」という,一瞬「?」と思ってしまう数値が並んでいますが,箱ひげ図をクリックするとここを参照していることがわかります。参照範囲に含まれていない「max-Q3,Q1-min」は,ひげを描画するときに使用されています。(誤差範囲のオプション⇒縦軸誤差範囲⇒「値の指定」をクリックすると確かめられますね。)

一方,「ローデータ」による「統計グラフ」の箱ひげ図を,もしHADが採用したとしたら,グラフをクリックしたときに表示される参照範囲は当然,「データ」シートに入力されたデータということになります。このことは何を意味するかというと,
1.もしも,箱ひげ図を出力したシートを新しいブックに移動した場合,参照範囲が見つからずグラフが再現されなくなる可能性がある。
2.もしも,データを編集した結果,参照先の数値が書き換わったとき,グラフが壊れてしまう可能性がある。
そんな失敗をするのは,よく注意しないからだ,と考えるならば,それは心理学の学習が足りませんね。人間は,ついうっかりするようにできています(断言)。そうであるならば,統計量をもとにグラフを描くほうが安全です。グラフと参照範囲が同じシートにあれば,シート単位で別のブックに移動しても,グラフは壊れません。
別の観点からも,棒グラフ積み重ねの方が扱いやすいことがあります。
まず,エクセルのグラフ機能による箱ひげ図では,X軸に変数名を表示することができません。さきほど貼り付けたグラフでは「凡例」の形で「Sepal.L」などを入れていました。しかし,論文に掲載する図としては適当ではありません。次に,Y軸の目盛りの指定で,最大値と最小値は設定できますが,目盛間隔を設定できません。最後に,箱ひげ図を他のグラフと組み合わせることができません。最後の点は,HADが,箱ひげ図にバイオリンプロットや散布図を重ねる機能を実現していることを考えれば,致命的です。
HADの箱ひげ図は進化した,と書いておきながら,結果を出していませんでした。こうなりますよ。見やすいようにちょっとグラフ設定をいじりました。

こういうの出したいときは,HADの設定をします。【HADの設定⇒グラフ設定⇒グラフ詳細設定】または【分析⇒グラフ設定】で次のフォームが出てきます。網掛けの部分に3つともチェックすると,上のような出力に。

包括的vs排他的
ところで,Excelの統計グラフで箱ひげ図を描くと,系列オプションの四分位数計算で「包括的中央値」か「排他的中央値」か選択するオプションがあります。これは何でしょう。以前から気になっていたので,この機会に調べてみました。
まず,マイクロソフトのサポートページでは,
包括的な中央値 N (データ内の値の個数) が奇数である場合に中央値が計算に含められます。
排他的な中央値 N (データ内の値の個数) が奇数である場合に中央値が計算から除外されます。
という,(?)な説明があります。よくわからないのでもう少し探してみたところ,
こんなページが見つかりまして,かなり詳しく説明されています。さらにここからリンクされているページで,
このページがたいへん見やすくて楽しい。曰く,四分位数とは,データをWの形に並べたときの曲がり角にあたる点なのだと。面白いではないか。こういう直観的な説明をしてくれる人って,すごいと思いますね。四分位数のイメージがつかめず困っている向きには,ぜひ一度お試しいただきたいと思います。英語ですけど。
これらのページで説明されているのは,四分位数ではなく,正確には「上側/下側ヒンジ」と言うのだそうですが,四分位数とほぼ等しい数値で,箱ひげ図の描画にはこの数値がよく使われるらしい。それで,ヒンジの算出方法に2種類あって,ひとつが Tukey の Inclusive hinge,もうひとつが Moore & McCabe(略してM & M)の Exclusive hinge である。用語の使い方と,マイクロソフトサポートページの説明内容から,エクセルの設定はこの2種類のヒンジの計算方法の選択を求めていると考えていいと思います。ざっくり説明すると,
たとえば,X = {1,2,3,4,5,6,7,8,9} というデータがあると,中央値は5。これは議論の余地なし。そこで,第一四分位数(Q1)と第三四分位数(Q3)をどうやって求めるかというのが問題で,
1.包括的中央値(ワークシート関数 QUARTILE.INC に対応)の場合
データの下半分を,Xlow = {1,2,3,4,5},上半分を,Xhigh = {5,6,7,8,9}と考えて(つまり中央値の5は両方に入る),それぞれ中央値を求め,それをQ1,Q3にする。Q1 = 3,Q3 = 7 になる。
2.排他的中央値(ワークシート関数 QUARTILE.EXC に対応)の場合
中央値のデータ「5」は使わずに(ここが違う),データの下半分を,Xlow = {1,2,3,4},上半分を,Xhigh = {6,7,8,9}と考えて,それぞれ中央値を求め,それをQ1,Q3にする。Q1 = 2.5,Q3 = 7.5 になる。
Excelで統計グラフを描くと,排他的中央値がデフォルトで選択されます。Rでは,この計算方法を選択することができて,type = 6とすると排他的中央値の結果と一致する。RのヘルプによればこれはSPSSと一致するらしい。そして,type = 7とすると包括的中央値の結果と一致する。こちらがRのデフォルト。結果を比較すると次のようになって,Excelの排他的中央値(Quantile.Exc関数)だけが,他の計算結果と異なる結果(黄色の網掛け部分)を出していることがわかります。(エラー値をそのまま入れていますが,Quantile.Exc関数は最小値,最大値を求めることができない仕様になっています。また,HADの出力は小数第3位まで表示しますが,ほかと表示形式をそろえてあります。)

ところで外れ値は
ところで,外れ値がプロットされないのが,積み上げ棒グラフ型箱ひげ図の弱点であることに変わりはありません。むりやり描きこんでみるとこんな感じになるのですが,どう考えても手間がかかり過ぎます。

ちなみにこれはどうやっているかというと,外れ値データを取り出して(この場合3つありました),それを1つずつ「散布図」グラフとして積み上げ棒グラフと組み合わせています。たぶん,VBAを使うともう少し違う形式でできるのだろうと思います。
Rを使ってバイオリンプロットやドットプロットを再現するのはもう少し時間が必要。 ggplot2 ライブラリの使い方をほとんど忘れていますので,しっかり復習してからにします。
追記
外れ値をドットで表示するためには,当然ですが,ひげの長さを変更する必要があります。Excelの quartile.inc 関数は,引数を0にしたときには字義通りの最小値(つまり Min 関数と同じ値),引数を4にしたときには字義通りの最大値(Max 関数と同じ値)を返します。なので,ひげの長さを四分位範囲×1.5 の範囲内で抑えるには,
1.四分位範囲を計算する。それに1.5を掛ける。
2.1の値を第三四分位数に足してひげの上限,第一四分位数から1の値を引いてひげの下限とする。
3.上限より大きい値を外れ値,上限以内の最大値をひげの上端の値とする。また,下限より小さい値を外れ値,下限以内の最小値をひげの下端の値とする。
4.3でもとめた上限と下限の値を用いてひげを描画する。また,3で求めた外れ値をひげの外側にプロットする。
のような手順を踏むことになります。
注意した方がよいのは,
1:どの方法が必ず正しい,とはいえないこと。
2:ネット上の記事には,「最小値」や「最大値」を,上述のひげの上端,下端の意味で用いている記事があり,字義通りの最小値や最大値ではない場合があること。(よく読まないとわからないことがある)
の2点でしょうか。上の方にリンクしてある「分位点2014」のサイトで,詳しく解説されています。
以上,追記しました。
