G検定 / 統計検定 データの視覚表現 #1

株式会社リュディアです。今回からデータの視覚表現、いわゆるインフォグラフィックについてまとめていきます。データを目で見てわかりやすくするための整理方法と考えてください。グラフのような絵になっているものもありますし表形式のものもあります。

今回は度数、累積度数、相対度数、累積相対度数とそのグラフ化についてまとめます。何となくならわかる、という方も今回のまとめでしっかりと理解してください。まず元データは以下の数字の集合を使いました。テストの点数をイメージしてもらえばよいかと思います。50個のデータがあります。

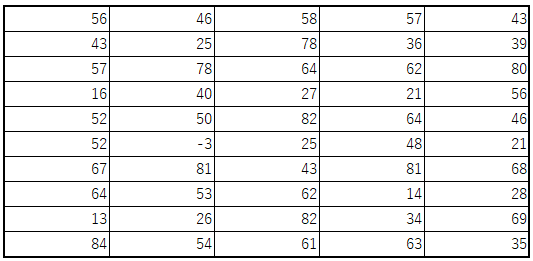
このデータを10点刻みで整理してみましょう。例えば0以上10未満には何人いるか10以上20未満には何人いるかという整理です。以下のようになります。

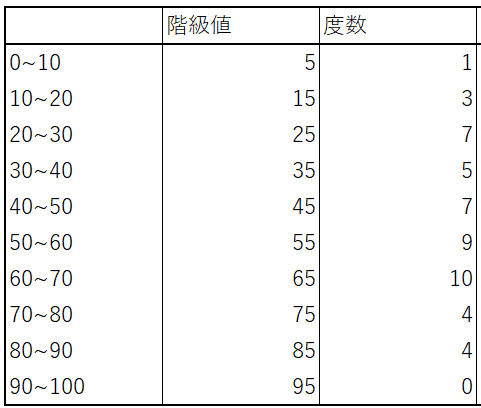
階級値は各階級の中央値としています。0~ 10 は 0以上10未満と理解してください。今回のデータでは 0 ~ 10 の範囲には1人ということになります。全部について整理したものを度数分布表と言います。

次に度数を順に累積していく累積度数を考え表に追記しました。左端の列の意味と若干ずれが発生しますが許してください。以下のようになります。

累積度数はわかりますね。度数を順に加算していきますので最後には全体を表す 50 になります。

今度は全体が 1 となるようにして度数と累積度数を相対的な値として表現することを考えます。それぞれ相対度数、累積相対度数と呼ばれる値です。表に追加した結果が以下になります。

ここまでで度数、累積度数、相対度数、累積相対度数の4つが登場しました。しっかりと区別できていますか？区別が怪しい方は再度最初から読み直すことをお勧めします。

ではこれらをグラフにしてみましょう。まず度数と相対度数を1つのグラフに表現してみます。度数は縦棒グラフ、相対度数を折れ線グラフで表現したものを見てみましょう。

度数を棒グラフ形式で表現したものをヒストグラムと呼びます。厳密には棒グラフとヒストグラムで違いはあるのですがここでは気にしないことにします。次に折れ線で表示している相対度数です。全体を50人という生データで扱うか全体を 1.0 という相対値で扱うかの違いだけなのでヒストグラムでも棒グラフでも同じ形状になります。グラフからもわかりますね。

同様に累積度数を棒グラフ、相対累積度数を折れ線グラフで表現したグラフを以下につけます。こちらも50人という生データを扱うか、50人という全体を1.0 とした相対値を扱うかの違いなのでグラフの形状が同じになることは理解できますね。

今回は度数、累積度数、相対度数、累積相対度数の数字の意味とそれぞれのグラフについてまとめました。基礎になる部分ですので用語の意味も含めしっかりと理解してください。

G検定 / 統計検定 データの視覚表現に関するまとめの続きは以下からどうぞ。

では、ごきげんよう。