高校数学 三角比(三角関数) #7

リュディアです。引き続き三角比(三角関数)について見てみます。今回は三角比（三角関数）と三角形の面積について見てみます。まず次の図の三角形の面積を計算してみてください。この直角三角形の斜辺の長さ c と角Bの大きさθは既知とします。もちろん sin, cos, tan は使用可能です。

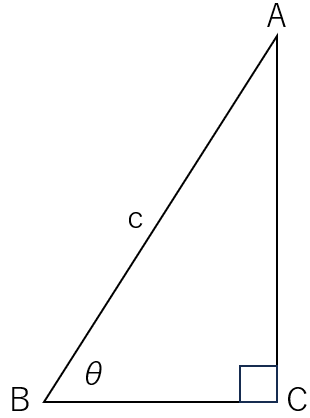
計算できましたか？次の図のようになります。底辺、高さを三角比を使って表現できたら三角形の面積は求まりますね。

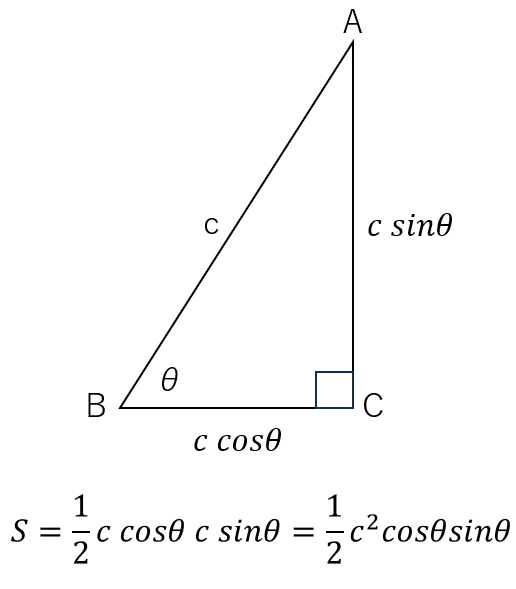
次に直角三角形ではない一般の三角形の面積を求める方法を考えてみましょう。次の図の三角形の面積を求めてみてください。三辺の長さa, b, c と角Bの大きさθは既知とします。

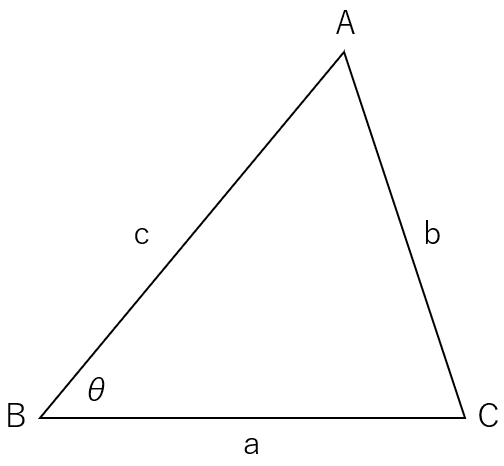
どうでしょう？できましたか。できなかった人は頂点Aから底辺に垂線を引いてください。これでできそうな気がしませんか？できなかった方は次の図を見てください。

補助線を一本引けば難しくないですね。この式は高校数学では公式として書かれていますが考えれば難しいことではないです。最終的にはテストで短時間に回答することを要求されるので覚えることができるなら覚えた方がいいですが、覚えるにしても図のイメージが頭にあればすぐに組み立てられそうです。自分で図のイメージを頭に入れてから頭のイメージを式として書いたら公式になった、という感じになるのが理想的だと思います。

では、ごきげんよう。