武蔵中の2021年の算数より～補助線を引くロジックを学ぶ～

正直芸がないなという出題ですが、武蔵中の2021年の算数の問題です。

正六角形ABCDEFがあり、その面積は10㎠です。BG＝EHで、GI：IC＝2：3です。このとき、三角形IDJの面積は何㎠ですか。(2021年度武蔵中)

これは次のような補助線を引いて解くことになります。
武蔵中は似た問題を延々と出し続けているので、「武蔵中対策」をしている生徒は難なく解けたのではないでしょうか。

ここで学びたいことは、「補助線の引き出し」についてです。
図形が苦手な生徒は、模範解答の補助線を見て「そんなの思いつかないよ」とか「あ、こうすれば解けるのね」とかで素通りしてしまいます。

しかし、出来るようになる生徒は「なぜこんな補助線を思いつくのか？」
「ひらめきなんて抽象的な理由では納得できない」という考えに至ります。

指導する側も「こうすれば解ける」ではなく、「なぜこのような補助線を引くことを思いつくのか？」を共有することが大事なのです。

武蔵中の問題ですと、正（偶数）角形は「対辺が並行」という性質があります。
よって中心から切る補助線を引くことで平行線を増やすことが出来、それにより「砂時計型」の相似を活用しやすくなるのです。

このように「補助線を引くロジック」を蓄積していくことが、他の生徒には「ひらめき」としてみえる能力の源なのです。

どの塾の教科書にも正六角形を「中心から切る」「砂時計型の相似を作り出す」問題は載っていますが、このように「なぜそのような補助線が有効なのか？」という「ロジック」として整理しておかなければ、「正八角形」などで出題された時に対応できないでしょう。

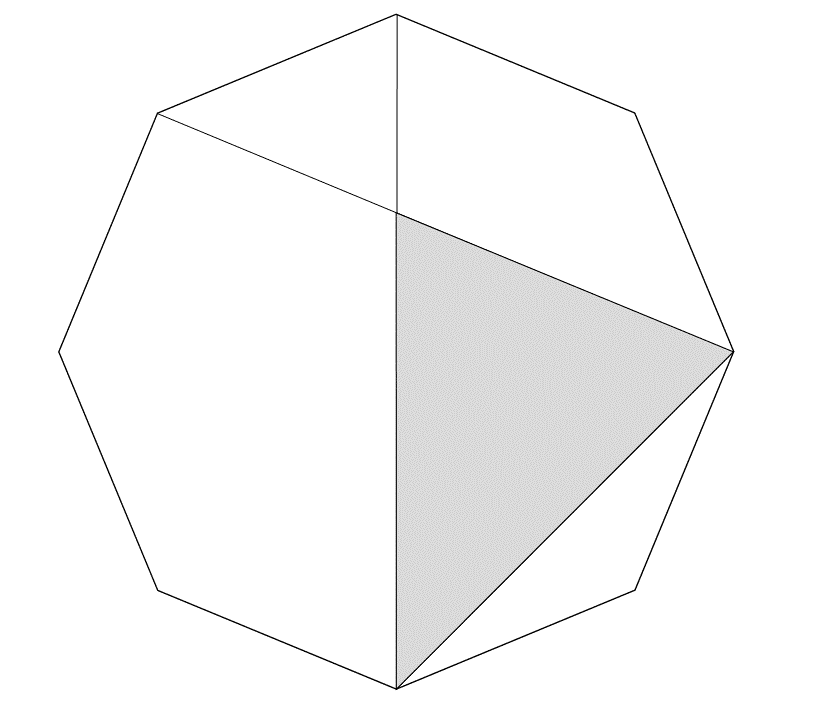
次の問題は2006年の東海中です。是非チャレンジしてみてください。（答えは最下部に記載）

「正８角形の面積は30平方センチ。斜線部の面積は？」

-------------------------------
答えは7.5平方センチメートルです。
-------------------------------