Von Neumann's information engine without the spectral theorem

Recently, our paper has been published in Physical Review Research.

Shintaro Minagawa, Hayato Arai, and Francesco Buscemi, Von Neumann's information engine without the spectral theorem, Physical Review Research 4, 033091 (2022).

The physical theories in our world are classical and quantum theories. However, are there any other theories in our world? Or, if not, why?

When I was a master's student, I had the following expectation:

Theories outside of quantum theory may violate the second law of thermodynamics. Conversely, there is a possibility that the second law characterizes quantum theory.

There have been several attempts to derive quantum theory from physical principles. For example, ref. [1] considered a certain correlation between separated two parties allowed under relativistic causality (called, "no-signaling principle"). However, they showed that a certain type of correlation allowed under no-signaling principle can be stronger than one can be achieved by quantum theory. This implies that there should be other principles in order to derive quantum theory. After a while, ref. [2] showed that "information causality", which includes no-signaling principle and is more general than it, restricts the above correlation to the same as quantum theory.

To consider thermodynamics in general theories, even outside of quantum theory, we may need to consider entropy in a fully operational narrative. In quantum theory, von Neumann determined entropy of a quantum state through a thought experiment in a way that depended on the mathematical structure of quantum theory [3] (explained below). Roughly speaking, our work reconstructs his thought experiment in a fully operational framework and explores some properties of entropy, not from the mathematical structure of theories, but as consequences of the second law of thermodynamics.

In order to discuss entropy even in theories away from quantum theory, we should describe theories outside of quantum theory. In our work, we use the following notions (these notions are common in the fields of general probabilistic theories, in short, GPTs (for the review, see e.g., refs. [4,5]) or operational probabilistic theories, in short, OPTs (for the review, see e.g., ref. [6])):

• a convex set $${\Omega}$$ is a "state space", and $${\rho\in\Omega}$$ is a state. The extremal points of $${\Omega}$$ are "pure states".

• "effects" $${e:\Omega\to\mathbb R_+}$$ are affine functions from a state to a positive real value.

• An effect $${u}$$ such that $${u(\rho)=1}$$ holds for all states is "unit effect".

• the set of effects $${\{e_j\}_{j\in J}}$$ is said to be a measurement if $${\sum_{j\in J}e_j=u}$$ holds.

• a "(single-system) instrument" is a set of maps $${s_j}$$ from a state to a (unnormalized) state and $${\sum_{j\in J}s_j(\rho)}$$ is a normalized state for any state $${\rho\in\Omega}$$.

(In our work, we do not have to consider the complete positivity of instruments, which seems to be a difficult problem, because, as explained in our paper, we only treat "measure-and-prepare" instruments.)

Here we introduce the important notion of "perfect distinguishable":
A family of states $${\{\rho_j\}_{j\in J}}$$ is said to be perfectly distinguishable if there is a measurement $${\{e_j\}_{j\in J}}$$ such that $${e_{j'}(\rho_j)=\delta_{jj'}.}$$

Quantum theory can be said to be a GPT with states and measurements described by complex Hilbert space. This mathematical structure allows all quantum states to have the following decomposition (the spectral theorem):
$${\rho=\sum_j q_j \sigma_j}$$
where $${\sigma_j}$$ are perfectly distinguishable pure (PDP) states (because they are orthogonal).

Von Neumann, a pioneer of the mathematical formulation of quantum theory, explicitly used spectral theorem to define "entropy of a quantum state" through a thought experiment, called "von Neumann's thought experiment of semipermeable membrane" [3]. A semipermeable membrane (in short, SPM) can separate perfectly distinguishable states (see fig. 1). By using it, we can separate $${N}$$ particles in a mixed state $${\rho=\sum_{j\in J}q_j\sigma_j}$$ into PDP states $${\sigma_j}$$ if we add work $${NkT\ln2 H(\{q_j\})}$$ where $${H(\{q_j\}):=-\sum_{j\in J} q_j\log_2 q_j}$$ is a Shannon entropy of a probability distribution $${\{q_j\}}$$ (for the detail of the separation process, please see ref. [3] or fig.2 in our paper) and $${k}$$ is Boltzmann constant. Then von Neumann defined entropy of $${\rho}$$ by $${H(\{q_j\})}$$.

FIG 1. An image of a semipermeable membrane. The membrane with holes only allows balls to pass through and cubes always bounce back. This means that this membrane perfectly distinguishes balls and cubes.

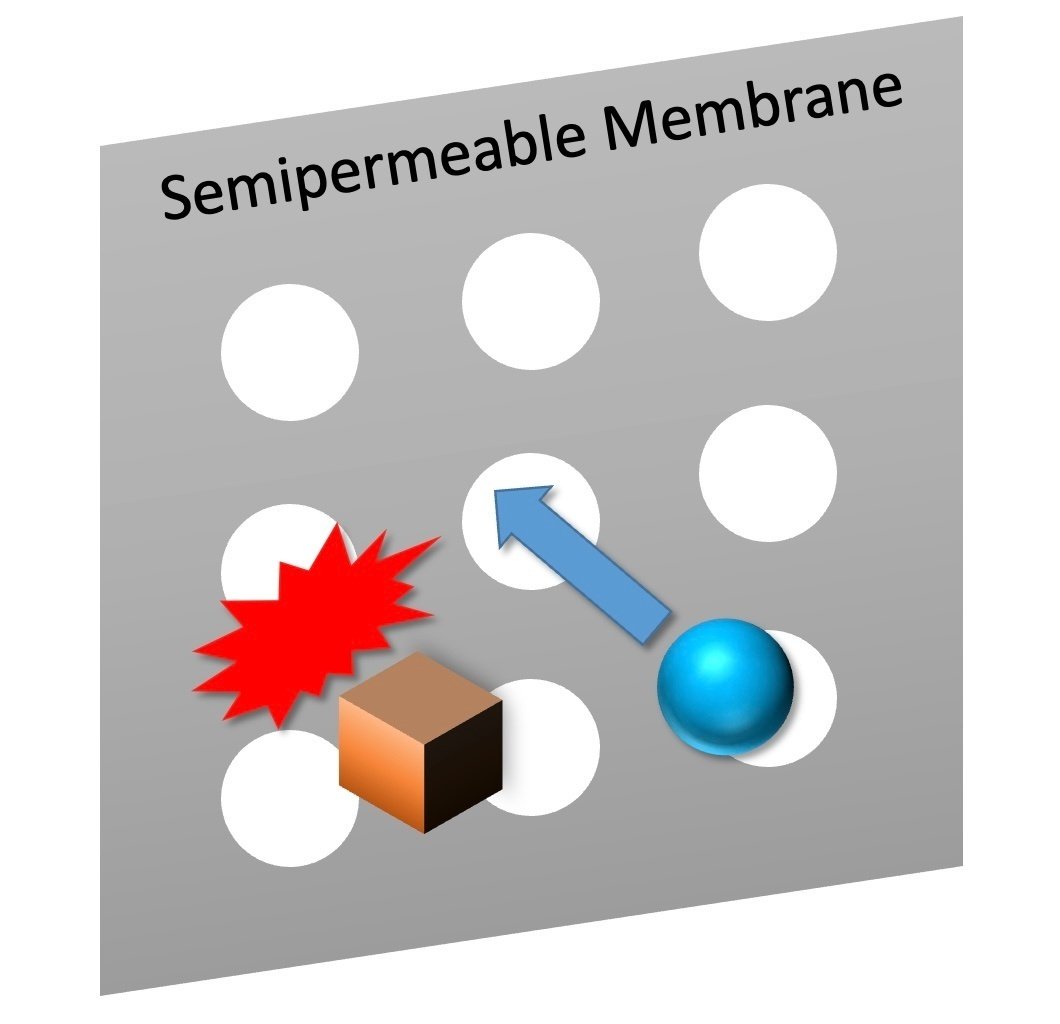
Generalizing this argument to GPTs has some problems. In particular, we address the following problems: how can we define entropy of a state $${\rho}$$ if it has multiple decompositions into PDP states? For example, for a state $${\rho}$$ with the following two decompositions:

$$
\rho=\sum_j q_j\sigma_j \qquad \mathrm{decompostion\:(1)}\\ \quad=\sum_i p_i\rho_i\qquad \mathrm{decompostion\:(2)},
$$

which one is the correct entropy, $${H(\{p_i\})}$$ or $${H(\{q_j\})}$$? Of course, there is no such problem in quantum theory thanks to the spectral theorem. However, in GPTs, this problem prevents us from defining entropy in the same way as von Neumann did.

We deal with this problem by making a simple modification: combine the separation process and the mixing process.

The mixing process can be implemented by using SPMs to mix the PDP states to make the initial state $${\rho}$$, which is nothing but the reversing of the separation process. Then, we separate $${\rho}$$ into the decomposition (1) and implement some operations and convert (1) to the decomposition (2), then we finally mix $${\sigma_j}$$ to make $${\rho}$$. If we implement these processes under the same temperature $${T}$$, the total work we can extract from this isothermal reversible cycle is $${\Delta W=NkT\ln2[H(\{q_j\})-H(\{p_i\})}$$.
The second law implies that $${\Delta W=0}$$, and we have $${H(\{q_j\})=H(\{p_i\})}$$. Therefore, even if there are multiple decompositions of a state, we can define entropy under the second law of thermodynamics.

[References]
[1] Sandu Popescu and Daniel Rohrlich, Quantum nonlocality as an axiom, Foundations of Physics 24, 379–385 (1994).
[2] Marcin Pawłowski, Tomasz Paterek, Dagomir Kaszlikowski, Valerio Scarani, Andreas Winter, and Marek Żukowski, Information causality as a physical principle,  Nature 461, 1101–1104 (2009).
[3] John von Neumann, Mathematical Foundations of Quantum Mechanics (Princeton University Press, Princeton, NJ, 1955).
[4] Peter Janotta and Haye Hinrichsen, Generalized probability theories: what determines the structure of quantum theory?, J. Phys. A: Math. Theor. 47 323001 (2014).
[5]  Martin Plávala, General probabilistic theories: An introduction, arXiv:2103.07469 (2021).
[6] Giacomo Mauro D'Ariano, Giulio Chiribella, and Paolo Perinotti, Quantum Theory from First Principles: An Informational Approach (Cambridge University Press, Cambridge, 2017).