
ベルンシュタインの定理証明してみた!
前回、有理数体$${\mathbb{Q}}$$が可算集合であることをみていきました。
このときに、用いたベルンシュタインの定理の証明をやっていきます。
目標:全単射をつくる
定理の主張を確認しよう
まずは、ベルンシュタインの定理の主張について、みていきましょう。
$$
集合A,Bについて,AからBへの単射およびBからA\\への単射がともに存在すれば,AとBの濃度が等しい
$$
濃度が等しいとは全単射が存在することです。この定理を用いることで、比較的易しく集合が可算集合であることなど調べることができます。
単射から全単射を構成したい
$${f:A \to B,g:B \to A }$$をともに単射としましょう。$${A}$$の元$${a}$$をひとつとって、$${f}$$でおくり、また$${g}$$で戻して、さらに$${f}$$でおくって…と繰り返すことを考えます。最終的に想定できるシナリオは
いつまでたっても終わらない
どこかでパタンと終了する
いま、集合$${A}$$をみっつの部分集合にわけて考えます。その前にひとつ用語を導入します。
行き先を”親”
$${a,a' \in A,~b,b' \in B}$$とします。$${b=f(a)}$$のとき$${a}$$を$${b}$$の親と呼び$${b \succ a}$$と書き、$${a'=g(b)}$$のとき$${b'}$$を$${a'}$$の親とよび$${a' \succ b'}$$と書きます。1.いつまでたっても終わらないのはずっと親がいる、2.どこかでパタンと終了するのは最後に親がいないと言い換えることができます。もうすこし、正確に説明していきましょう。
集合をみっつに分ける
2.はもう二つに分かれます。
いつまでたっても終わらない
どこかでパタンと終了する
$${A}$$で終了する
$${B}$$で終了する
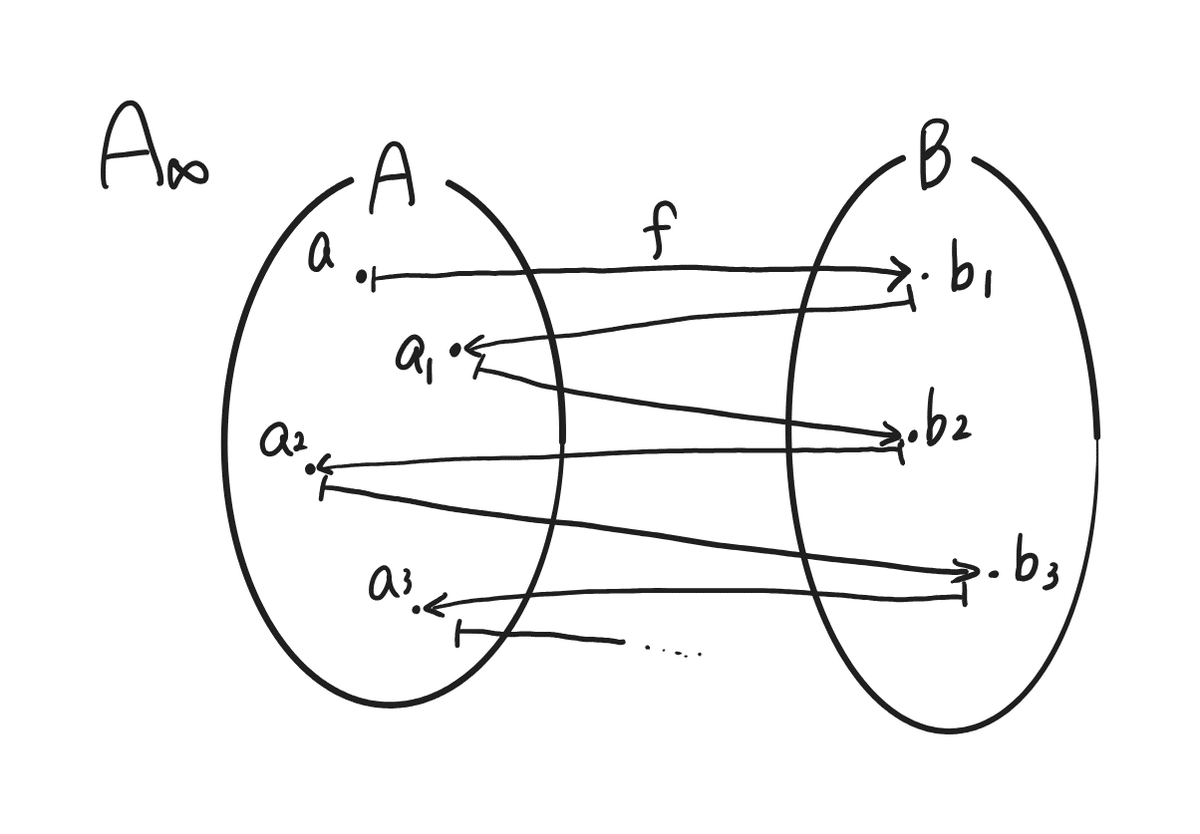


イメージしたことを式に落としてみましょう。
$$
A_{\infty}=\{a \in A|a \succ b_1 \succ a_1 \succ b_2 \succ a_2 \succ …,\} \\
A_A=\{a \in A|a=a_1 \succ b_1 \succ … \succ b_{n-1} \succ a_n,a_nには親がない\} \\
A_B=\{a \in A|a=a_1 \succ b_1 \succ … \succ a_{n-1} \succ b_n ,b_nには親がない\}
$$
と定義すると、これらは$${A}$$の部分集合です。さらにこれらは明らかに非交和です。また、$${f,g}$$は単射だから、これらの列は一意に確定します。
$$
A=A_{\infty} \cup A_A \cup A_B \\
(A=A_{\infty} \amalg A_A \amalg A_B)
$$
これとまったく同様に$${B}$$についてもみっつに分割できます。
$$
B=B_{\infty} \cup B_A \cup B_B
$$
全単射を構成する
$${A,B}$$をそれぞれ三つの部分集合に分けれることができました。これらの定義から
$$
f(A_{\infty})=B_{\infty}, ~~ f(A_A)=B_A ,~~ g(A_B)=B_B
$$
がわかります。これらは集合の制限を考えれば、全単射です。したがって、写像$${h:A \to B}$$を
$$
h(x)=\begin{cases}
f(x)~~~~~~~x \in A_{\infty} \cup A_A \\
g^{-1}(x) ~~x \in A_B
\end{cases}
$$
と定めることができて、$${h}$$は全単射です。

よって、ベルンシュタインの定理が証明できました。
参考文献
