
note 56: 分光器設計 その6(波長分解能)_edit1-190913
note 56: 分光器設計 その6(波長分解能)_edit1-190913
前回の「迷光」と並んで、極めると超難しい「波長分解能」を今回書いてみる。
「波長分解能」は、波長純度とも呼ばれる。
回折格子の分解能:島津製作所
https://www.shimadzu.co.jp/products/opt/guide/05.html
その前に、
note 50: 分光器設計 その1_edit1-190828
https://note.mu/lingmu0788/n/n85ec6aba2524
この記事で、Bを説明したがもう少し詳しく説明しておく。
B. リレー光学系としての機能
分光器光路説明-190827.JPG

光学系の像の大きさを求めるときに、”有限遠”と”無限遠”の二種類がある。
”有限遠”とはレンズの大きさに対して対象の物体(物点)が近い場合で、
”無限遠”とはレンズの大きさに対して対象の物体(物点)が遠い場合をさす。
カメラレンズは普通、”無限遠”で設計されている。
”無限遠”の言葉どおり、対象の物体はレンズから無限に遠くに離れていると仮定する。
そうすると、フィルム(最近は半導体イメージセンサーのCCDやCMOSセンサー)のどの高さに像を結ぶかは、以下の簡単な式で表される。
y=f・tan θ
y:像の高さ
f:レンズの焦点距離
θ:光軸と物点のなす角度

ツェルニターナー型分光器の場合結像ミラーに入射される光は回折格子のよて分光された平行光になる。従って、”無限遠”の光学性だと言える。
さて、本題の「波長分解能」について説明する。
光はレンズによってどこまで小さいスポットに集光可能だろうか?
これは言い方を変えると、隣接した点を結像位置でどこまで区別できるかと同じである。
以下の図は近接した物点が結像された場合の像プロファイルの例である。
物点の点と点が離れている場合は、像面でくっきりと点像が分かれた見える。しかし、点の間隔がどんどん近づいてくると像面でのボケが無視できなくなり、ついには以下の例の様にY軸プロファイルの二点の山が分離できずに重なってくる。
その5-像のぼけ.PNG

先の、分光器光路説明-190827.JPG のA. の場合はY軸上に波長分散(分光されている)が起きているので、位置が波長に換算できる。という事は像の空間分解能が波長分解能に換算できることになる。
回折格子の分解能:島津製作所
以下、引用
https://www.shimadzu.co.jp/products/opt/guide/05.html
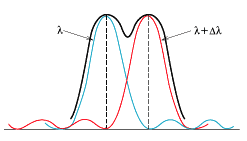
2つの近接した波長λとλ+Δλの2 本のスペクトル線があるとき、どのくらい小さいΔλまでを2本のスペクトルとして区別できるか、という能力を表わすものが分解能です。一般に、回折格子(Gratings:グレーティング)の回折光は回折限界で定義される有限の幅をもっています。レーリーの基準(Rayleigh criterion)によれば、図3のように波長λのスペクトルの第1 極小値の位置に波長λ+Δλのスペクトルの最大値がくるときを分解できる限界と定義しています。このときの分解能λ/Δλは、回折格子の幅をW とすると、
その5-回折格子の分解能-2.png
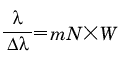
その5-回折格子の分解能_図.png
で表わされます。ここでN ×W は回折格子の溝の総本数を意味します。
しかし実際に回折格子を他の光学素子と併用する場合、たとえば分光器に組み込んで使用する場合などは、他の光学素子(レンズやミラー等)の収差や不完全さ、あるいは光源やスリットの大きさのため、スペクトル線はさらに広がります。このため、分解できるスペクトルの波長差Δλは大きくなるので、一般に光学系の分解能は”その5-回折格子の分解能-2.png”:式で表わされる回折格子単体の分解能より悪くなります。
NxWを多くすれば(回折格子の溝本数を多くすれば)いくらでも波長分解能が良くなるように見えますが、上記理由で値は有限になります。
波長分解能が低い分光器ではラフに設計してもそれなりの値は得られるが、波長分解能数nm以下程度になると、回折格子を含めた全ての光学素子の性能や分光器マウント方法、マウント精度等が波長分解能に効いてくる。
特に高分解能が求められる場合は分光器を二つつなげて分光するダブルモノクロが用いられる時もある。しかし、光量を非常にロスする暗い分光になる為、光源の照射パワーを上げたり、検出器の感度を上げたるする工夫が必要になってくる。
