二階微分のライプニッツ表記の分数的性質
一階微分は分数と見なせることが良く知られている事実だが、実は分数であることまで良く知られていないのが残念な事実である。さらに、二階微分は分数と見なせないことも事実だが、あまり論じられてないのが寂しい事実である。
結論から言うと、まず二階微分のライプニッツ表記は分数と見なせない。仮に二階微分を分数として扱えたところで嬉しいことが見当たらないから、結局は現状維持される、というオチになる。
1 一階微分が分数である故
形式的には、関数$${ y = f(x) }$$に対するライプニッツ表記$${ \displaystyle \frac{dy}{dx} }$$が$${ dy }$$を$${ dx }$$で割った商を表す分数表記に見える。「微分は分数であるか」というのは、「本当に商と解釈して良いのか」という疑問である。問題の本質は$${ dy }$$の定義と理解となる。
問題を簡単にするため、性質の良い好都合な関数のみで考える。逆関数も含めて2階以上の微分可能な実数関数で考える。区間的に微分可能で良く、微分不能な点が多少存在しても良いが、その点を除いた区間て考える。
そもそも微分が分数と見なせるか否かを議論するため、分数のように書くライプニッツ表記$${ \displaystyle \frac{dy}{dx} }$$で微分を表すのは控える。原則ラグランジュ表記$${ f'(x) }$$を用いるが、微分変数を明記するためにオイラー表記$${ Df(x), D_x f(x) }$$も使う。
一般に、一階微分の概念はグラフ上における曲線の接線の傾きと関連付けられる。定量的には関数$${ y = f(x) }$$に対し、微分を(式1.1)で定義できる。高校数学で登場する定義式である。
(式1.1) $${ \displaystyle f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} }$$
図形的には、まず実関数$${ f(x) }$$は x-y 平面上では$${ \{(x,y) | y = f(x) \} }$$の形で点の集合を与える。微分可能な実関数の場合は点集合が滑らかな曲線に見える。曲線上から任意の2点$${ T = (x,y) = (x, f(y)) }$$と$${ S = (x+\Delta x, y + \Delta Y) = (x+\Delta x, f(x+\Delta x)) }$$を取ると、この2点を通る直線を曲線の割線(secant)を定義できる。点Sを点Tに近付けて一致した瞬間の割線の極限を点Tにおける接線(tangent)と定義できる。
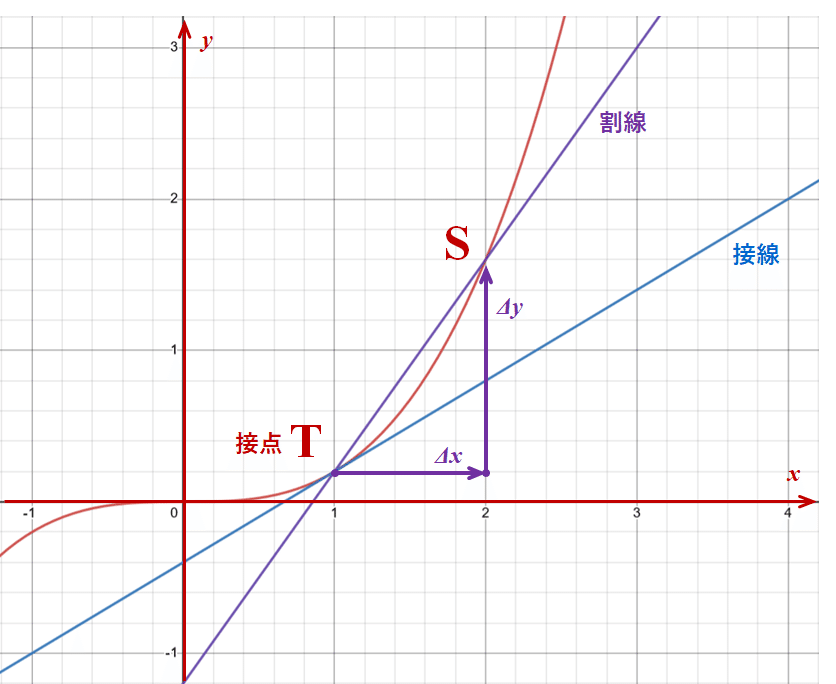
このとき、割線の傾きは$${ \displaystyle \frac{\Delta y}{\Delta x} = \frac{f(x + \Delta x) - f(x)}{\Delta x} }$$で与えられ、式(1.1) の極限を取る対象になっている。式(1.1) の極限 $${ \displaystyle \lim_{\Delta x \to 0} }$$は点Tを点Sに近付けることを表し、式(1.1) が定義する極限値は接線の傾きを表す。こうして微分が接線の傾きと結び付けられる。
注意すべきは、この時点で$${ dx }$$や$${ dy }$$を定義してない。したがって、割線のところで$${ dx }$$や$${ dy }$$を定義したため$${ \displaystyle \frac{\Delta y}{\Delta x} }$$とは書けるが、$${ \displaystyle \frac{dy}{dx} }$$は未定義な要素を含むために、以上の定義だけでは書いて良いかは判断できない。

実際のところ、接点を原点とする dx-dy 座標系を定義すると、接線方程式は$${ dy = f'(x) dx }$$になるため、実数の除算として$${ f'(x) = dy \div dx = \displaystyle\frac{dy}{dx} }$$と書ける。接線上にあれば$${ dx }$$は任意に取れるが、$${ dx = \Delta x }$$と尺度を合わせた場合、割線までの距離$${ \Delta y }$$と、接線までの距離$${ dy }$$の違いが良く分かる。
注意として、この方法で定義される$${ dx }$$は座標値であり、通常の実数値を表す。$${ dy }$$も同様で、$${ dx }$$の関数であり、その関数値が実数値である。これらは微分に関連付けられる「微小」である必要もなければ、0に近づける必要もない。
$${ \Delta x }$$を0に近づける話はあくまでも割線を接線に近付ける$${ \Delta x }$$側の話であって、$${ dx }$$は切り分けて考えるべき。$${ \displaystyle \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \frac{dy}{dx} }$$であって、 $${ \displaystyle \lim_{\Delta y \to 0} \Delta y = dy }$$でもなければ、$${ \displaystyle \lim_{\Delta x \to 0} \Delta x = dx }$$でもない。$${ \displaystyle \lim_{\Delta x \to 0} \Delta x = 0 }$$であるし、特に$${ dx \neq 0 }$$である。
2 二階微分が分数でない故
二階微分は一階微分で得られた導関数をさらに微分したものである。ラグランジュ表記では$${ f''(x) = \big(f(x)\big)'' = \Big(\big(f(x)\big)'\Big)' }$$となる。
(式2.1) $${ \displaystyle f''(x) = \lim_{\Delta x \to 0} \frac{f'(x + \Delta x) - f'(x)}{\Delta x} }$$
ここで、一階微分が$${ dx }$$と$${ dy }$$の分数であることから、二階微分$${ \displaystyle \Big( \frac{dy}{dx} \Big)' }$$は商の微分と言える。そうすると二階微分は積の微分に帰着してから分解できる。
(式2.2) $${ \displaystyle f''(x) = \Big( \frac{dy}{dx} \Big)' = \Big( dy \cdot \frac{1}{dx} \Big)' }$$
$${\displaystyle \; = (dy)' \cdot dx^{-1} + dy \cdot ( dx^{-1} )' }$$
$${\displaystyle \; = (dy)' \cdot dx^{-1} + dy \cdot ( -dx^{-2} ) \cdot (dx)' }$$
$${\displaystyle \; = \frac{(dy)' \cdot dx - dy \cdot (dx)'}{(dx)^2} }$$
ここで$${ (dy)' }$$は$${ dy }$$を$${ x }$$で微分することのため、単純に$${ \displaystyle \frac{d(dy)}{dx} }$$と展開される。この$${ d(dy) }$$は$${ y }$$に対する$${ dy }$$の作用を再度適応したものに等しいため、意味的には$${ d^2y }$$と書くべき因子である。$${ d^2y = d(dy) }$$を採用した場合は、続けて計算できる。
(式2.3) $${ \displaystyle f''(x) = \frac{(dy)' \cdot dx - dy \cdot (dx)'}{\underset{\;}{(dx)^2}} }$$
$${\displaystyle \; = \frac{\displaystyle \frac{d(dy)}{dx} \cdot dx - dy \cdot \frac{d(dx)}{dx}}{\underset{\;}{(dx)^2}} }$$
$${\displaystyle \; = \frac{\displaystyle \frac{d^2y}{dx} \cdot dx - dy \cdot \frac{d^2x}{dx}}{\underset{\;}{dx^2}} }$$
これを(式2.4)または(式2.5)に整理することもできる。
(式2.4) $${ \displaystyle f''(x) = \frac{\displaystyle d^2y \cdot dx - dy \cdot d^2x}{\underset{\;}{dx^3}} }$$
(式2.5) $${ \displaystyle f''(x) = \frac{d^2y}{dx^2} - \frac{dy}{dx} \cdot \frac{d^2x}{dx^2} }$$
ここで、(式2.3)から(式2.5)の中には既に$${ d^2y }$$が登場しているため、$${ f''(x) }$$を$${ \displaystyle\frac{d^2y}{dx^2} }$$と定義した上で分母分子を別々に解釈した場合、$${ d^2 y }$$が異なる複数の意味を持つようになり、曖昧になる。このため、二階微分のライプニッツ表記$${ \displaystyle \frac{d^2y}{dx^2} }$$は$${ d^2y }$$と$${ dx^2 }$$の商を表す分数とは見なせない。
$${ \displaystyle \frac{d^2y}{dx^2} }$$はあくまでも$${ \displaystyle \frac{\displaystyle d\Big[\frac{dy}{dx}\Big]}{dx} }$$と解釈すべきであり、外側の微分対象である$${ \displaystyle \frac{dy}{dx} }$$を商と見なすからこそ、商の微分が適応され、$${ \displaystyle \frac{dy^2}{dx^2} }$$の他に、$${ \displaystyle \frac{1}{dx} }$$に作用する項が現れる。事実に反するが、もし(式2.5)の第2項が無ければ、$${ \displaystyle f''(x) = \frac{d^2y}{dx^2} }$$という期待する形になるのは容易に確認できる。
形式的な計算順で考えると、$${ d }$$の作用対象に$${ \displaystyle\frac1{dx} }$$、もしくはもっと単純に$${ dx }$$が含まれる場合、安易に交換してはならないことになる。事実に反するために、$${ \displaystyle \frac{d^2y}{dx^2} }$$の意味を交換前後の両方に割り当てる定義は叶わない。
(式2.6) $${ \displaystyle \Big(\frac{d}{dx}\Big)^2 \big[ y \big] = \frac{d}{dx} \Big[\frac{d}{dx} \big[ y \big] \Big] = [[y]']' = y'' }$$
$${ \; \displaystyle \neq \frac{1}{dx} \cdot \frac{d}{dx} \Big[d \big[ y \big] \Big] = d^2y \div (dx)^2 = \frac{(d^2y)}{dx^2} }$$
https://www.researchgate.net/publication/322787770_Extending_the_Algebraic_Manipulability_of_Differentials では$${ d^2y }$$を$${ d(dy) }$$となる定義を採用し、一定の利用価値も見出している。
Bartlett, Jonathan & Khurshudyan, Asatur. (2018). Extending the Algebraic Manipulability of Differentials. Dynamics of Continuous, Discrete and Impulsive Systems Series A: Mathematical Analysis. 26. 217-230.
それでも、現実では二階微分の方が利用価値が高いため、現在では$${ \displaystyle \frac{d^2y}{dx^2} = \Big(\frac{d}{dx}\Big)^2 }$$に割り当てるのが一般的であり、二階以上のライプニッツ表記に関しては分数表記をするが分母分子を分けて考えない定義にしている。
3. 接放物線と二階微分
一階微分は幾何的に接線、すなわち接直線と結びついていた。接線方程式は一次近似を与える。これに対し、零階微分は参照点の値そのものと言える。この類推により、二階微分は参照点で接する放物線、すなわち接放物線に関連付けられるとのが予想できる。これらを纏めると、(式3.1)になる。これらは点$${ a }$$周りのテーラー展開を途中で打ち切った近似式になっている。
(式3.1)零次近似:$${ y = f(a) }$$
(式3.2)一次近似:$${ y = f(a) + f'(a) \cdot (x−a) }$$
(式3.3)二次近似:$${ y = f(a) + f'(a) \cdot (x−a) + \displaystyle\frac{f'(a)}{2} \cdot (x−a)^2 }$$
それぞれの最高次項を残し、低い項を右から左側に移項すると、各階の微分を係数とする式を得られる。
(式3.4)零階微分:$${ y = f(a) }$$
(式3.5)一階微分:$${ y - f(a) = f'(a) \cdot (x−a) }$$
(式3.6)二階微分:$${ y - f(a) - f''(a) \cdot (x−a) = \displaystyle\frac{f''(a)}{2} \cdot (x−a)^2 }$$
左側を$${ y }$$に何かの作用を施したものに置けたら、最高次項に比例した式を作られる。
(式3.7)$${ d_0 y = f(a)\cdot (d_1x)^0 }$$:$${ d_0 y = y }$$
(式3.8)$${ d_1 y = f'(a) \cdot (d_1x)^1 }$$:$${ d_1 y = y - f(a) = \delta y }$$
(式3.9)$${ d_2 y = f''(a) \cdot (d_1x)^2 }$$:$${ d_2 y = 2\big(y - f(a) - f'(a)\cdot (x-a)\big) }$$
こうなれば、各比例係数は割算として表現できるようにはなる。二階微分は
(式3.10)$${ \displaystyle f(a) = d_0 y \div d_1x^0 = \frac{d_0 y}{\underset{\;}{dx^0}} }$$
(式3.11)$${ \displaystyle f'(a) = d_1 y \div d_1x^1 = \frac{d_1 y}{\underset{\;}{dx^1}} }$$
(式3.12)$${ \displaystyle f''(a) = d_2 y \div d_1x^2 = \frac{d_2 y}{\underset{\;}{dx^2}} }$$
ここで$${ d_1 }$$は通常の微分$${ d = d^1 }$$と見なせて、$$ d_0 $$は恒等的であるため$${ d^0 }$$と見なせる。しかし、$${ d_2 \neq d^2 }$$であるため、区別が必要である。二階微分は$${ d^2 }$$が2回の微分を表すのに対し、$${ d_2 }$$は二次近似において定数項のみならず一次項まで引いた二次的な差分を表すため、ここでは「二次微分」と呼ぶことにする。
これにライプニッツ表記を適応した場合、$${ \displaystyle \Big(\frac{d}{dx}\Big)^2 y = d_2 y \div dx^2 = \frac{d_2 y}{dx^2} }$$と書ける。さらに拡張された$${ d^2y = d(dy) }$$を使えば、$${ d_2 y = d^2y - \displaystyle\frac{dy}{dx} d^2x }$$のような式も得られる。しかし、$${ d_2 y }$$が$${ d^2y }$$以上に特殊で、式変形で現れ難く、興味深い話に繋がるのを見かけていない。
