そして理詰め探しの旅へ

前の記事の続きです。こっちは相当マニアック。

(おまけの考察)

最後の部分がどうもうまく理詰めにしきれませんでした。(小ループ禁を理詰めっぽく表現するということについては未発展の部分が多いと感じています。白マスが余るタイプの破綻は大体「はいはい市松で問題なし」ってなるのですが……。)

小ループ禁は市松の傾斜という点では問題が生じないため、(最低1本は通るという条件を外した)市松理論は小ループ禁に対して効力を持ちません。よって小ループ禁絡みの表現を何かしら使っていく必要がありますが、ここでどうにも上手い表現の仕方が未だによくわかっていないのです。

しかし、完全理詰めがモットーの自分が諦めて2択を引くなんて……嫌です。何がなんでも理詰めをでっち上げてやろうという気分になります。もう速さなんてどうでもいいんです。いざ理詰め探しの旅へ。

(議題)

下図のパターンが破綻する要因を明らかにし、理詰めっぽい流れをでっち上げる。

とりあえず簡易盤面を作ります。

理詰めでっち上げでは何らかの破綻や確定を先に見つけて後付け的にそれを説明する論理をくっつけるというのがよくやる自分のやり方なのですがここでは盤面が小さいので確定箇所を全検してみることにします。といってもこれは唯一解の問題なので確定箇所は全てであり、それでは意味がないので一旦小ループ禁をルールから外し、それでもなお確定する場所を考えてみることにします。

小ループ禁を無視して作ることのできる盤面は黒マスの置き方2通りで試すと以下のようになり(線も×もない場所は引くパターンと引かないパターンが両方生きている状態)、共通部分を取り出すことで得られる情報は小ループ禁を使わずに説明できる要素です。

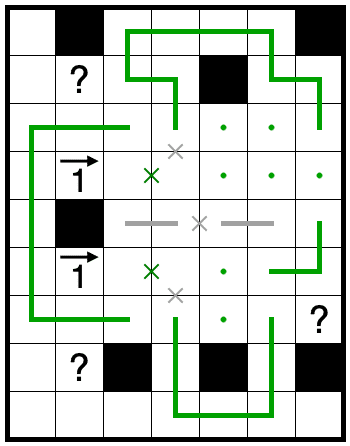
初めに→1の外側の×は簡単なチェインです。手筋でもいいかもしれません。

辺から飛び出す線は中央が白の辺1×3から言えます。使える機会は多いですがあまり役に立ちません。

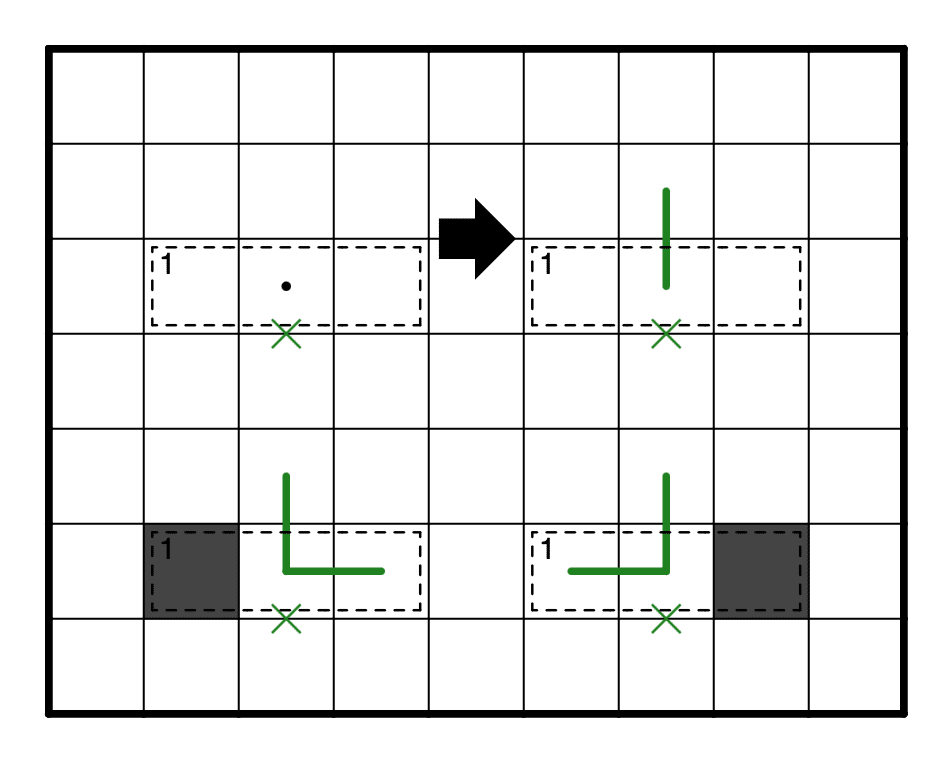
以下の形をもう少し考察すると上と横から線が1本ずつ出ることがわかります。(市松から導けます。)

ということはここは本数定理です。

最後のは……なんだろう。例えば以下の本数定理からシンプルループの市松手筋をチェインに組みこんで導出できますね……。まぁとりあえずこれでよし……、と。

どうやら小ループ禁を使わざるを得ないようなのでもう少し考えます。破綻する片方のパターンは左と下が上の線を回収せずに繋がってしまうことが要因で、その道のりもはっきりとわかっています。ならばその道に沿って分断を考えてあげれば何かしらが見えてこないかなと考えてみました。

図のような領域分けについて、簡単なチェインないし先程の本数の変形、あるいは内外を絡めて見ると青の境界を越える線は0本か2本です。また市松を考えると(どちらの領域から考えても良いです)青の境界を越える線と黄色の境界を越える線は同じ本数でなければいけません。更に小ループ禁より青と黄色の境界から最低2本の線が抜けます。

以上より青線の境界を抜ける線は2本とわかり、正しい解にたどり着けました。

理詰め探しの旅という名のでっち上げ、以上です！こういった考えを続ける中で新たな理詰めが発展することを願いながら今日も先読み0の理詰めにこだわり続けています。