チェインって何ですか?
本記事はペンシルパズルI Advent Calendar 2022の13日目です。
こんにちは、lilvaです。Twitterパズル歴3年です。本日は13日、成宮由愛ちゃんの年齢……以下略。アドベントの記事を書くのも3年目、今年はチェインのざっくりとしたイメージ、用語説明、使い方をlilvaのわかる範囲内で説明します。何か間違っている箇所がありましたらご連絡下さい。
チェインの用語まとめとしては既にSP1さんの以下の記事があります。この記事でも参考にさせて頂いております。
1. チェインのイメージ
まず用語を整理する前に、私の持つ大雑把なチェインのイメージの話をします。
1.1 2択の連鎖
チェインとは一言で説明するなら「2択の連鎖」で決まる箇所を見つける考え方です。HoDoKu生成の数独を例に説明します。
例1: X-Chain
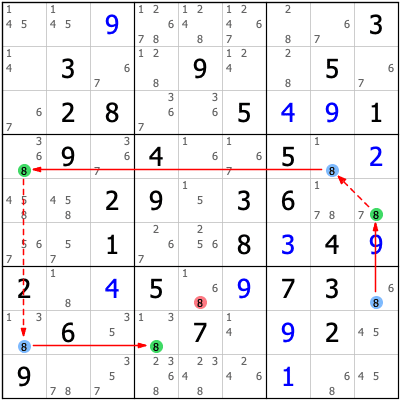
8の入りうる箇所に注目すると、
◯ 9列目のR5C9,R7C9の2択
◯ 4行目のR4C1,R4C8の2択
◯ 8行目のR8C1,R8C4の2択
などがあります。
R7C9が8でないとすると、R5C9が8→R4C8は8でない→R4C1が8→R8C1は8でない→R8C4が8というように情報が連鎖し、R7C9かR8C4の少なくとも一方には8が入ることがわかります。いずれにせよR7C5に8は入りません。
例2: XY-Chain

入る候補が2択のマスに注目すると、
◯ R2C6の5か7の2択
◯ R9C6の2か5の2択
◯ R9C5の2か9の2択
◯ R7C4の7か9の2択
などがあります。
R2C6が7でないとすると、R2C6が5→R9C6は5でない→R9C6が2→R9C5は2でない→R9C5が9→R7C4は9でない→R7C4が7というように情報が連鎖し、R2C6かR7C4の少なくとも一方には7が入ることがわかります。いずれにせよ赤丸の7は全て除くことができます。
このように連鎖する2択を使って決まる箇所を探す考え方がチェインです。実用的には2択をいくつか見つけた上で、その中で連鎖するような組み合わせを探してあげれば良いです。
1.2 強リンクと弱リンク
もう少し理論寄りの説明では、チェインは“強リンク”と“弱リンク”を繋いだものと言われます。
2択が連鎖する条件に注目すると、異なる2択の端が「同時に成り立たない」関係にあることが条件だとわかります。用語としてこの「同時に成り立たない」関係を“弱リンク”、逆の「片方は成り立つ(=2択)」の関係を“強リンク”と呼び、強リンクと弱リンクを交互に繋ぐことで情報が連鎖します。
例1: X-Chain

R7C9かR5C9は8(強リンク)
R5C9かR4C8は8ではない(弱リンク)
R4C8かR4C1は8(強リンク)
R4C1かR8C1は8ではない(弱リンク)
R8C1かR8C4は8(強リンク)
以上のチェインにより、R7C9かR8C4に8が入ることがわかります。
例2: XY-Chain

R2C6は5か7(強リンク)
R2C6かR9C6は5ではない(弱リンク)
R9C6は2か5(強リンク)
R9C6かR9C5は2ではない(弱リンク)
R9C5は2か9(強リンク)
R9C5かR7C4は9ではない(弱リンク)
R7C4は7か9(強リンク)
以上のチェインにより、R2C6かR7C4に7が入ることがわかります。
このように強リンクと弱リンクを交互に繋いだものをチェインと呼びます。数独(や美術館など)では同じ列に2つ以上入らないという条件から弱リンクが張り巡らされた構造になっていて、実用上は「2択の連鎖」のイメージ、強リンクをいくつか見つけてその中で弱リンクで繋がる組み合わせを探すことになります。
「2択の連鎖」は主にチェインが活きる数独、美術館といったパズルでの解く上での考え方、一方「強リンク弱リンク」は実用よりも理論、チェインを仕込む作者的な考え方と言えるかもしれません。
2. リンクとチェイン
最近、他のパズルにチェインの考え方を応用する場合、強リンクと弱リンク以外も考えた方がより統一的に扱えるのではと思っているのですが、ここでは特に数独や美術館などで解くのに役に立つ範囲、強リンクと弱リンクに絞った説明をします。
2.1 リンク
2つの要素の関係で非自明なもの、片方の真偽が即座に確定してしまわないものをリンクと呼ぶことにします。
①強リンク

2つの要素A, Bが同時に偽にならない関係であることを強リンクと呼びます。私が図に書き込む際には実線や赤線を使います。また右下のようにAが偽ならBは真、Bが偽ならAは真(対偶)という関係になっています。
②弱リンク
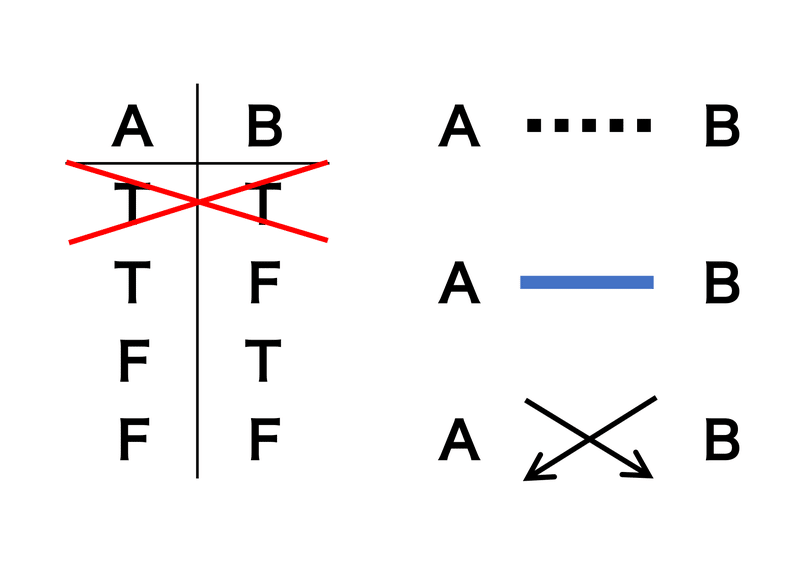
2つの要素A, Bが同時に真にならない関係であることを弱リンクと呼びます。私が図に書き込む際には点線や青線を使います。右下のようにAが真ならBは偽、Bが真ならAは偽(対偶)という関係になっています。
2.2 チェイン
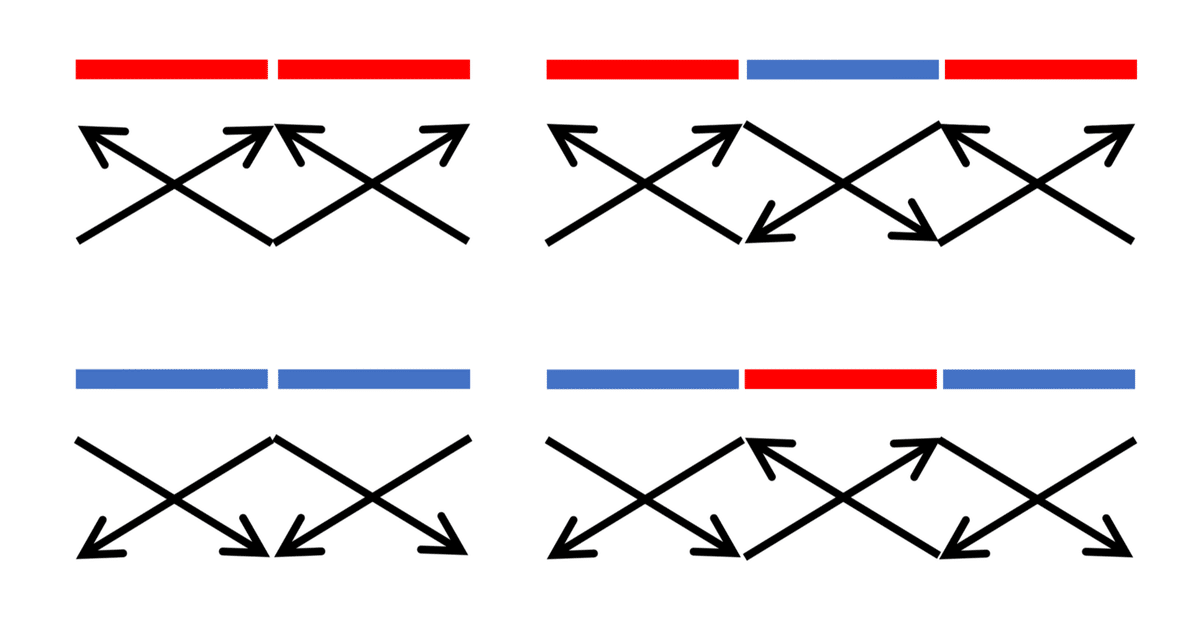
複数のリンクを直列に繋いだもので何かしら新たに分かる情報があるものをチェインと呼ぶことにします。チェインは強リンクと弱リンクを交互に繋いだものになります。

上の図は情報の伝播を視覚的に表したものです。強リンク同士、弱リンク同士は繋がりませんが、交互に繋ぐことで強弱強は強リンクとして、弱強弱は弱リンクとして使えることがわかります。
3. 使用例
3.1 長さが奇数のループ

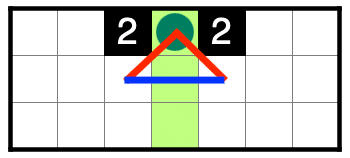
②隣接禁による弱リンク
③三連禁による強リンク
へやわけの例です。チェインはリンクを強弱交互に繋ぐ必要があるので右上のマスを両端とした弱強弱のチェインと考えます。この時、右上のマスは自分自身との弱リンクになるので必ず偽、白マスになります。
逆に自分自身との強リンクが得られる場合には必ず真になります。以下の美術館はその一例です。
強リンク、弱リンクが並ぶ場所で情報の伝播は途切れています。HoDoKuではDiscontinuous Nice Loopと呼ばれます。
3.2 長さが偶数のループ
全ての場所で強弱交互になっているようなチェインの輪っかが見つかった時には1のように直接確定することはありませんが、別の見方で分かることがあります。

上のチェインについて、一番下の弱リンクを無視すると、強弱強弱強なので強リンクとみなせます。つまり一番下の弱リンクがあった場所に新たに強リンクが得られます。同様に他の弱リンクがある場所にも強リンクが、逆に強リンクがある場所には弱リンクが得られます。
これをうまく利用できる例の一つが、元々の弱リンクが3つ以上のものについて同時に成り立たない関係である場合です。チェインに含まれる2つのいずれかが真なので残りは必ず偽になります。数独のX-Wing、美術館の回廊などはその利用例とも言えます。(ただし、上限下限制約で扱った方が便利です。Fishと呼ばれます。)

HoDoKuではContinuous Nice loopsないしAIC loopsと呼ばれます。
3.3 別にループでなくても良い
強弱交互にリンクを繋げば両端のリンクが得られるという見方のほうが都合の良い場合があります。

既に出てきたXY-Chainの例です。これはR2C6の7からR7C4の7までのチェインにより2つの間に強リンクが得られることで、共通して排除できるマスから候補を除くことができます。チェインの両端と排除される7は弱リンクの関係にあるので、これは1を重ね合わせたものと考えることもできます。HoDoKuではこのように排除マスが複数にわたるチェインはAICと呼ばれます。
4. 終わりに
以上、lilvaによるチェインのお話でした。主に数独や美術館といった弱リンクの多いパズルで確定箇所を見つける方法の1つとして、あるいはリンクを繋いで確定を仕込むためのツールとして、チェインと慣れ親しんでもらえればと思います。
なお本記事は元々書いていたチェインの小話が乗っ取られて出来た記事です。裏側の世界に本来書きたかった内容があるのでもしよければそちらも是非。
