
Taichiでscaled_dotproduct_attentionを実装する
TaichiでのLLM学習・実行に興味があり、scaled_dotproduct_attentionを実装してみました。
Taichiとは
Taichiは、GPU並列処理をPythonで記述できるライブラリです。コンピューターグラフィックスでの利用が想定されています。
scaled_dotproduct_attentionとは
Transformerで使用されるAttentionメカニズムです。
クエリ(Q)、キー(K)、バリュー(V)を用いて、入力シーケンス内の各位置での重要な情報を捉えるために使用されます。
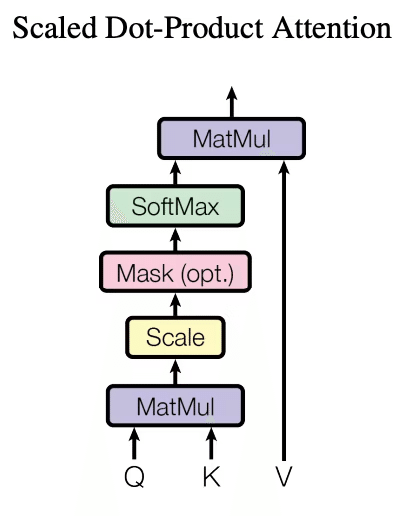
https://arxiv.org/abs/1706.03762 より
Causal mask
図の「Mask (opt.)」に対応する処理です。
Attentionメカニズムが将来のトークンを参照しないように制約を加えるために使用されます。
マスキング方法
Attentionスコア(キーとクエリのドット積)に対して、未来のトークンに相当する位置のスコアを非常に小さい数値(例えば、-∞など)に設定します。その結果、ソフトマックス関数を適用した時に、これらの位置の重みが実質的に0になり、未来のトークンの影響を排除します。
マスクされたAttentionスコアの例
[[0.06 -inf -inf -inf -inf -inf -inf -inf]
[0.87 0.39 -inf -inf -inf -inf -inf -inf]
[0.24 0.45 0.90 -inf -inf -inf -inf -inf]
[0.16 0.10 0.30 0.77 -inf -inf -inf -inf]
[0.67 0.57 0.37 0.15 0.56 -inf -inf -inf]
[0.65 0.72 0.62 0.02 0.24 0.73 -inf -inf]
[0.82 0.10 0.46 0.17 0.59 0.87 0.94 -inf]
[0.68 0.81 0.52 0.65 0.31 0.66 0.71 0.41]]※行列の形状はシーケンス長さ×シーケンス長さであり、トークン数(GPT4なら最大32kトークン)に依存するので、実際はもっと巨大な行列になります。
参考コード
nanoGPTが実装の参考になりました。
https://github.com/karpathy/nanoGPT/blob/master/model.py#L52
# manual implementation of attention
att = (q @ k.transpose(-2, -1)) * (1.0 / math.sqrt(k.size(-1)))
att = att.masked_fill(self.bias[:,:,:T,:T] == 0, float('-inf'))
att = F.softmax(att, dim=-1)
att = self.attn_dropout(att)
y = att @ v # (B, nh, T, T) x (B, nh, T, hs) -> (B, nh, T, hs)
作成したコード
コードはここにあります。
import taichi as ti
import math
import time
import numpy as np
np.set_printoptions(suppress=True)
np.set_printoptions(formatter={'float': '{:.2f}'.format})
IS_DEBUG = True
# IS_DEBUG = False
BACKEND = ti.gpu
ti.init(BACKEND, debug=IS_DEBUG)
# パラメータ設定
batch_size, head_size, sequence_size, embedding_size = 1, 2, 4, 8
# Taichi fields
Q = ti.field(dtype=ti.f32, shape=(batch_size, head_size, sequence_size, embedding_size))
K = ti.field(dtype=ti.f32, shape=(batch_size, head_size, sequence_size, embedding_size))
V = ti.field(dtype=ti.f32, shape=(batch_size, head_size, sequence_size, embedding_size))
out = ti.field(dtype=ti.f32, shape=(batch_size, head_size, sequence_size, embedding_size))
@ti.kernel
def init_attention(q:ti.template(), k:ti.template(), v:ti.template(), out:ti.template()):
# ダミーデータの生成
for I in ti.grouped(q):
Q[I] = ti.random()
K[I] = ti.random()
V[I] = ti.random()
out.fill(0) # 出力の初期化
init_attention(Q, K, V, out)
@ti.func
def max2d(matrix:ti.template()) -> ti.f32:
"テンソル全体の最大値を計算"
max_val = 1e-10
for i,j in ti.ndrange(matrix.n, matrix.m):
max_val = ti.max(max_val, matrix[i,j])
return max_val
@ti.func
def softmax2d(mat:ti.template()):
"softmaxを計算して、引数の行列を書き換える。"
n,m = mat.n, mat.m
mat_max = max2d(mat)
for s,_s in ti.ndrange(n,m):
mat[s, _s] = ti.exp(mat[s, _s] - mat_max) # 指数関数を計算する前に最大値を引く
for s in range(n):
sum_exp = 0.0
for _s in range(m):
sum_exp += mat[s, _s] # _s についての和を計算
for _s in range(m):
mat[s, _s] = mat[s, _s] / sum_exp # _s についての和で割る(正規化)
@ti.kernel
def scaled_dotproduct_attention(q: ti.template(), k: ti.template(), v: ti.template(), out: ti.template()):
"""
Parameters
---------------------
q,k,v,out : tensor with shape [... s e]
s : sequence
e : embedding
"""
assert q.shape == k.shape == v.shape == out.shape
# 形状からsequence_sizeとembedding_sizeを取得
upper_dims = ti.static(q.shape[:-2]) # 最初の2次元
sequence_size, embedding_size = ti.static(q.shape[-2:]) # 最後の2次元
for I in ti.static(ti.ndrange(*upper_dims)):
mat = ti.Matrix([[-1e9] * sequence_size for _ in ti.ndrange(sequence_size)], ti.f32)
# attention scoreを計算
for s, _s in ti.ndrange(sequence_size, sequence_size):
if s < _s: continue # Causal mask : s <= _s だけを計算
mat[s, _s] = 0.0
for e in range(embedding_size): mat[s, _s] += q[I, s, e] * k[I, _s, e]
mat[s, _s] *= (1.0 / ti.sqrt(embedding_size))
if IS_DEBUG: print("att: ", I, mat)
# Softmax
softmax2d(mat)
if IS_DEBUG: print("softmax(att): ", I, mat)
# 出力の計算
for s, _s, e in ti.ndrange(sequence_size, sequence_size, embedding_size):
out[I, s, e] += mat[s, _s] * v[I, _s, e]
scaled_dotproduct_attention(Q, K, V, out)
ti.sync()
time.sleep(0.1)
print("out: ", out)値が正しいか検証
`torch.nn.functional.scaled_dot_product_attention`と比較しました。
import torch
out_torch = torch.nn.functional.scaled_dot_product_attention(Q.to_torch(), K.to_torch(), V.to_torch(), attn_mask=None, dropout_p=0
# , is_causal=False
, is_causal = True
)
print("out: ", out_torch.numpy())
print("diff: ", out.to_numpy()-out_torch.numpy())結果:diffはほぼ0なので大丈夫そうです。
diff: [[[[0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00]
[0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00]
[0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00]
[0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00]]
[[0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00]
[0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00]
[0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00]
[0.00 0.00 0.00 0.00 -0.00 -0.00 -0.00 -0.00]]]]解説
テンソルの軸形状
テンソル「Q,K,V,out」の軸形状は「… s e」を想定しています。
… : なんでも。主に「b h」(バッチ軸、ヘッド軸)を想定。
s : シーケンス軸
e : Embedding軸
計算式とコードの対応

一時変数の注意点
並列実行されるforループ内に記述した一時変数「mat」は、並列実行時に各スレッドブロック(Thread Block。GPU上で並列に実行されるスレッドの論理グループ)で別々に作成されます。
そのため、一時変数「mat」の軸は「… s e」ではなく「s e」でよいです。
(というより、Taichiスコープ内ではfieldのように動的にメモリ確保する変数は定義できません。組み込み型のVector, Matrixなら定義できます。)
mat = ti.Matrix([[-1e9] * sequence_size for _ in ti.ndrange(sequence_size)], ti.f32)工夫した点
ランク多態性
さまざまな階数のテンソルを処理できる性質を私はランク多態性と呼んでいます。(正式な用語ではないと思います。)
こちらのスレッドの発言をそのまま使わせてもらっています。
基本的にQ,K,V,outのテンソル形状は「b h s e」軸を想定しています。
しかし、scaled_dot_product_attentionの処理で必要な軸(つまりインターフェース)は「s e」軸だけです。
そこで、それ以外の軸形状は分離しました。そのため、様々な形状「… s e」のテンソルをこの関数だけで処理できるようにしています。
実装のポイント:以下のようにti.staticの処理でテンソル次元を取得することで、Pythonスコープでのコンパイル時に軸を取得して、コンパイルエラーを回避しています。
upper_dims = ti.static(q.shape[:-2]) # 最初の2次元
sequence_size, embedding_size = ti.static(q.shape[-2:]) # 最後の2次元Pythonスコープ・Taichiスコープの参考
https://docs.taichi-lang.org/docs/language_reference
Causal Maskは必要な箇所だけ計算
素直にマスキング処理するなら、Attentionスコアをすべて計算した後に、マスキングして-infを代入するかもしれません。
しかし、Attentionスコアは-infで初期化して、必要な箇所だけ計算した値を代入するようにしています。
必要な箇所だけ計算を行うことで無駄な計算を減らしています。
# attention scoreを計算
for s, _s in ti.ndrange(sequence_size, sequence_size):
if s < _s: continue # Causal mask : s <= _s だけを計算
...Softmaxは指数関数を計算する前に最大値を引く
指数関数の指数から最大値を引いています。
mat_max = max2d(mat)
for s,_s in ti.ndrange(n,m):
mat[s, _s] = ti.exp(mat[s, _s] - mat_max) # 指数関数を計算する前に最大値を引く指数関数の出力値が大きくなりすぎてオーバーフローする問題の対策として一般的な手法らしいです。
改善点
以下の点はまだ詰め切れていないので改善が必要です。
ループの中のifをなくす
並列処理部分は極力if文を少なくして、Warpの並列実行が阻害されないようにする必要があります。
Warpとは、NVIDIAのCUDAアーキテクチャにおいて、32個のスレッドで構成される最小の実行単位です。同一のwarp内のスレッドは、命令を同時に(SIMD形式で)実行します。そのため、if文による条件分岐が存在すると、異なる実行パスをたどるスレッドが生じ、それにより実行がシリアライズされ、効率が大幅に低下します。
Causal Maskの処理でif文を使っていますが、インデックスの組を生成する時点で不要な組が生成されないように修正した方が良さそうです。
# attention scoreを計算
for s, _s in ti.ndrange(sequence_size, sequence_size):
if s < _s: continue # Causal mask : s <= _s だけを計算所感
Taichiは初見だったので、色々思うところがありました。
処理内容が分かりやすい
私はテンソル操作は不慣れで、コードを見ても具体的にどのような計算をしているのかすぐにピンときません。
たとえば以下のコードを見て思うのは…
att = (q @ k.transpose(-2, -1)) * (1.0 / math.sqrt(k.size(-1)))🤔💭
@ってどんな計算?(行列積です。"… i j" @ "… j k" -> "… i k")
transpose(-2, -1)?テンソルの転置って?(rearrange(t, '... i j -> ... j i')です)
Taichiならインデックスで指定するので、テンソルのどの要素を計算しているのか分かりやすいです。
mat[s, _s] += q[I, s, e] * k[I, _s, e]🤔💭
シーケンス位置s,_sの違う要素同士を掛け算して合計している!
学習
Taichiは学習曲線が急峻で、動くコードを書けるようになるまでがやや大変でした。
ウェブ上に情報が少ないためか、ChatGPTとClaudeはあまりよいコードの書き方を教えてくれませんでした。ランク多態性などの書き方は自分で編み出す必要がありました。
そのため結構学習が必要だったのですが、拙作「Code-lets」に書き方をメモしながら学習を進めました。

JupyterLabでスニペットを動かして、動作したコードをPostしていく感じです。
「あれはどのように書くんだっけ?」となった時に、素早く描き方を探すことができて、学習の記録場所としては結構良かったです。
