
人工知能入門:バックプロパゲーション
この記事は、私がメルマガ「週刊Life is beautiful」の2023年1月24日号に書いた記事です。今年になってからメルマガを読み始めた読者にも読んでいただきたいので、Noteとして公開します。
私は、難しいことを誰にでも(可能であれば中学生にでも)分かりやすく解説することに、使命感さえ感じています。
私自身、今でも勉強が大好きで色々なことを勉強していますが、その過程ではなかなか理解できずに苦労することもあります。そんな場合には、さまざまな教材に目を通して勉強しながら、時間をかけて手探りで答えを見つけるしかありません。特に私にとっての「理解」とは、単に公式や定理を覚えたりすることではなく、「直感的に理解する」ことなので、とても手間がかかります。
そんな中でも、「直感的な理解」に至るまで最も苦労したのは相対性理論です。最初に読んだブルーバックスの書物のような一般向けの解説書には、相対性理論から導かれる「時空の歪み」や「時間の遅れ」などが興味深く書かれていますが、最も重要な「アインシュタインはどうやってその理論に辿り着いたのか」がちゃんと書かれておらず、フラストレーションが溜まるばかりでした。
大学に入り、(私は電子通信学科でしたが)物理学科の相対性理論の授業を受けましたが、難しい数式ばかりで、数式はかろうじて追えるものの、「直感的な理解」とはほど遠いものでした。それから数年後に、ロシア人が書いた相対性理論の解説書(残念ながら題名は忘れてしまいました)を読み、目から鱗が取れるように「直感的な理解」が進み、本当に感動したのですが、同時に「こんなに分かりやすい解説方法があるのに、なぜ今まで誰もしてくれなかったのだろう」と不満に思ったことを良く覚えています。
「なぜ分かりやすい解説書が少ないか」に関しては、諸説考えられますが、ブルーバックスのような「解説書」は、「どうせ素人には理解出来ないのだから、相対性理論から導かれる不思議な現象を知ってもらえれば十分」と考えており、逆に、物理の教科書となると「直感的な理解よりも、数式や公式をツールとして使いこなせるように教育する」ことに重点が置かれており、私が求めている「相対性理論の直感的な理解」というニーズに応えてくれる書物が、ほぼ存在しない状況になっているのだと私は見ています。
今回、私が取り上げる「人工知能」に関しても同じことが起こっています。素人向けの入門書には、人工知能によりどんなことが可能になったのか、などが読者の興味をそそるように書かれていますが、ここ10年の急速な進歩のきっかけとなったディープラーニング(深層学習)とバックプロパゲーション(誤差逆伝播法)がどんな仕組みなのかに関しては、表面的な解説しかありません。
一方、実際にディープラーニングの教科書を見ると、PyTorchやTensorflowの使い方や実際の応用例にばかりページ数を割いており、もっとも肝心なバックプロパゲーションの「直感的な理解」の助けにはなってくれません。
私自身も漠然と、バックプロパゲーションがどんな仕組みで動くのかは理解していましたが、それを自分で実装することが可能になるほどの「直感的な理解」には至っていませんでした。私自身がそんな状態では、表面的な解説は出来たとしても、本当の意味で「分かりやすい解説」が出来るわけもなく、少し悩んでいました。
しかし、先日、TeslaのAIチームを率いていたAndrej Karpathyの[The spelled-out intro to neural networks and backpropagation: building micrograd」というタイトルのビデオを見た時に、それが「直感的な理解」に至り、ようやく「分かりやすい解説」をする準備が整ったと言えるようになりました。
機械学習の基礎になっているのは、パーセプトロン(Perceptron)と呼ばれる計算機で、数式にすると、以下のような形をしています。
output = g(w1 * x1 + w2 * x2 + ... + wN * xN + b)
x1, x2, ..., xN は、この計算機への入力(N個)で、w1, w2, ..., wNは、計算機が持つそれぞれの入力に対する重み付けのパラメータで、bは入力とは無関係に足されるパラメータです。g はアクティベーション関数と呼ばれ、(一般的に)入力が大きいと1に、小さいと0(もしくは-1)を出力する階段状の関数で、「スイッチ」のような役割を果たします。
別の言い方をすれば、1つのパーセプトロンは、N個の入力(x1, x2, ...xN)に対して1つの出力をしますが、その計算にN+1個のパラメータ(w1, w2, ..., wN と b)を使うのです。

パーセプトロンは、複数の入力を持ち、特定の条件を満たした時のみ「発火する(スイッチが入る)」脳みその中のニューロンをモデルにしており、複数のパーセプトロンをネットワーク状に組み合わせたものを、ニューラルネットワークと呼びます。
ネットワーク状とは言っても、M個のパーセプトロンを使って、N個の入力に対してM個の出力をする「レイヤー」を作り(その場合、一つのレイヤーは (N + 1) * M 個のパラメータを持ちます)、そんなレイヤーを複数繋ぎ合わせてニューラルネットワークを構成するのが一般的です。こんな構造にしておくと、レイヤーごとの計算は、単純な行列計算になるため、GPUなどのハードウェアを使った並列実行が可能になるのです。
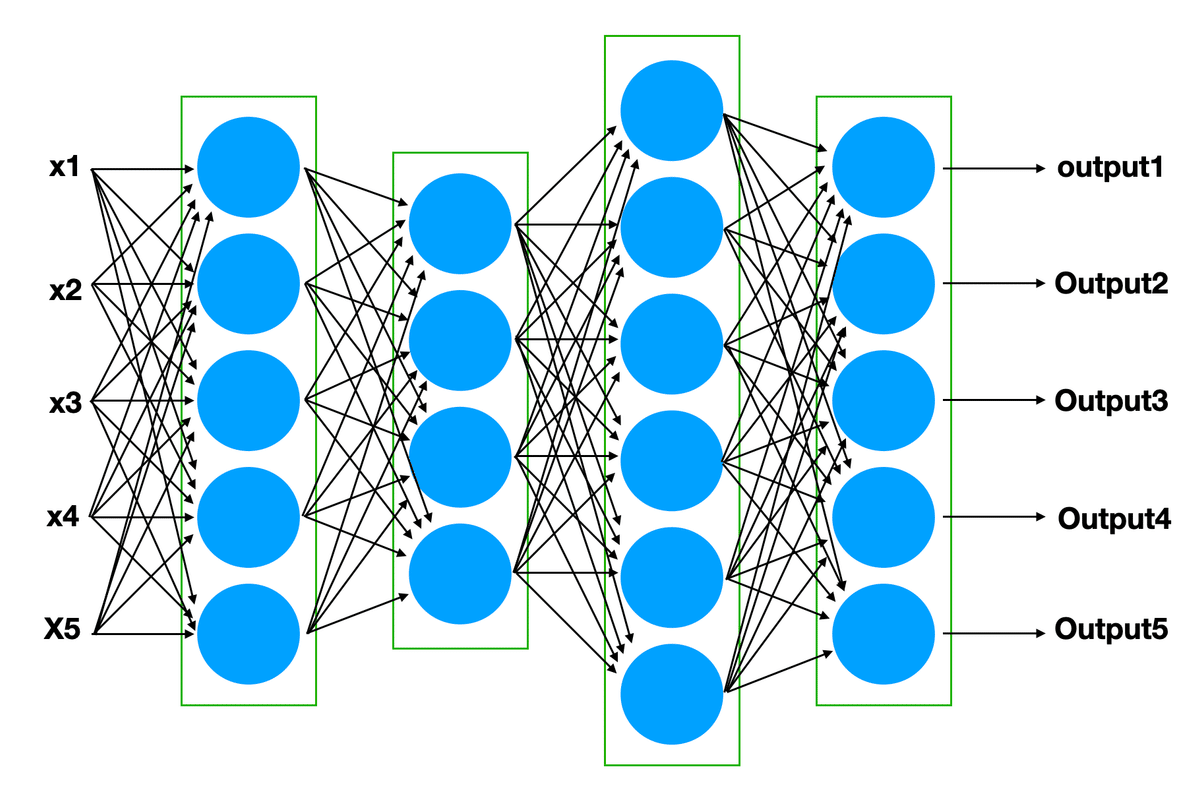
ここ10年ほどの人工知能においては「深層学習(deep Learning)」という言葉が使われますが、「深層」とは、レイヤーが複数あることを示しています。
そうやって作ったニューラルネットワークに仕事をさせるには、入力に対して適切な出力をするように(例:入力した画像に写されているのが猫か犬かを判断するように)、ニューラルネットワーク内部にあるたくさんのパラメータ(それぞれのパーセプトロンのw1, w2, w3, …)を適切な値に設定する必要があります。
そのために行うのが、「機械学習」というプロセスです。入力に対して期待した通りの出力が得られるかどうかを調べながら、少しづつ、それらのパラメータを変化させて(改良して)行くプロセスです。
そのプロセスに使われる手法が、Gradient Decentと呼ばれる手法です。まず、入力に対する出力がどのくらい間違っているかを数値化する関数 loss function を定義し、それぞれのパラメータをわずかに変化させた時に、loss functionの出力がどのくらい変化するか(微分係数=グラフを描いた場合の傾き)を求めた上で、その傾きに応じて、それぞれのパラメータを少しづつ変化させて、loss functionの出力を徐々に下げて行く、という手法です。
最も単純な例として、
output = w1 * x1 + w2 * x2というパーセプトロンのみがニューラルネットワークにあり、教育データとして、入力が[1, 0]の場合は出力1, 入力が[0, 1]の場合は出力0があったとします(ここでは、計算を簡単にするために、アクティベーション関数はなかったことにします)。loss functionとしては、得られた答えと期待する値の差の絶対値を使うことにします。
w1とw2のそれぞれの初期値が0.5だった場合、
- 入力[1,0]に対する出力は0.5(期待されている出力は1)。loss funcitionの出力は 0.25
- 入力[0,1]に対する出力は0.5(期待されている出力は0)。loss funcitionの出力は 0.25となります。
入力[1,0]の場合、loss functionの出力を減らす(期待されている出力に近づける)にはoutputを上げる必要があります。 output の式をそれぞれ、w1, w2で微分すれば、x1(=1), x2(=0) となり、w1を増やせば良いことが分かります(w2を変化させても効果はありません)。
入力[0,1]の場合は、loss functionの出力を減らすには、outputを下げる必要があるので、同様に考えて、w2 を減らす必要があることが分かります。
この情報を元に、w1 と w2 を少しだけ(例えば 0.1)変化させ、再度 loss function を計算して w1とw2を変化させる方向と量を決めることを繰り返し、徐々に loss function の出力を期待された通りのものに近づけて行くのです。
この手法が、一つのレイヤーのパーセプトロンを持つニューラルネットワークの学習に使えることは以前から知られていましたが、同様の手法が、複数のレイヤーから構成される複雑なニューラルネットワークにも適用できるようにする、バックプロパゲーションというテクニックが、一気に人工知能の技術を向上させたのです。
複数レイヤーあっても Gradient Decent が可能なことを示すために、
p = w1 * x1 + w2 * x2 + b1
q = w3 * x1 + w4 * x2 + b2
output = w5 * p + w6 * q + b3のように、最初のレイヤーで p, q を計算し、2番目の複数のレイヤーで、p, q から output を計算ケースを考えてみます。
パラメータ、w5、w6、b3 を少しだけ変化させた場合の output の変化(傾き)は、それぞれ p, q, 1 であることは、output の式をそれぞれ w5, w6, b3 で微分すれば一目瞭然です。
w1, w2, b1 に関しては、式pをそれぞれ w1, w2, b1 で微分すると、x1, x2, 1 という数値が得られますが、これは p の変化を表しているだけです。output の変化を知るには、式outputをpで微分して得られる値 w5 を掛け合わせる必要があり、それぞれ x1*w5, x2*w5, w5 という数字が得られます。これは、outputのw3による微分は、outputのpによる微分とpのw3による微分を掛け合わせれば良いという微分の法則から来ていますが、直感的には、二つの傾きが重なり合っていると考えても良いし、p を output で展開すれば、
output = w5 * (w3 * x1 + w4 * x2 + b2) + w6 * q + b3となるので、これを w3, w4, b2 で微分すれば、x1*w5, x2*w5, w5 になると考えても結構です。
こんな風に、それぞれのパラメータがloss functionに与える影響(微分係数)を、ネットワークの最終レイヤーから後ろ方向に計算していくことにより、どんなに複雑なニューラルネットワークであっても、それぞれのパラメータをどちら方向にどのくらい変化させれば良いのかを知ることができるようになり、これにより、それまで不可能だった複数レイヤーから構成されるニューラルネットワークの学習が可能になり、一気に人工知能がさまざまな分野で応用されるようになったのです。
Andrej Karpathyのビデオを見る前から、複数の書物を読み、ニューラルネットワークの仕組みも、バックプロパゲーションの存在も知っていましたが、レイヤーを遡って微分係数を求める際に、実際にどう計算すれば良いのかがどの資料にも明記されておらず、そこにフラストレーションが溜まっていたのですが、Karpathy氏が実際にコーディングをしてみせることにより、上に書いたように、単にレイヤーごとの微分係数を掛け合わせれば良いことが直感的に理解でき、そのフラストレーションが解消できたのです。
