大学入試数学今週の一題#4
久々の投稿💦
では、前回の問題のおさらいから

いわゆる、存在範囲の問題です。
問題を読んで気づいてほしいのは次の事実です。
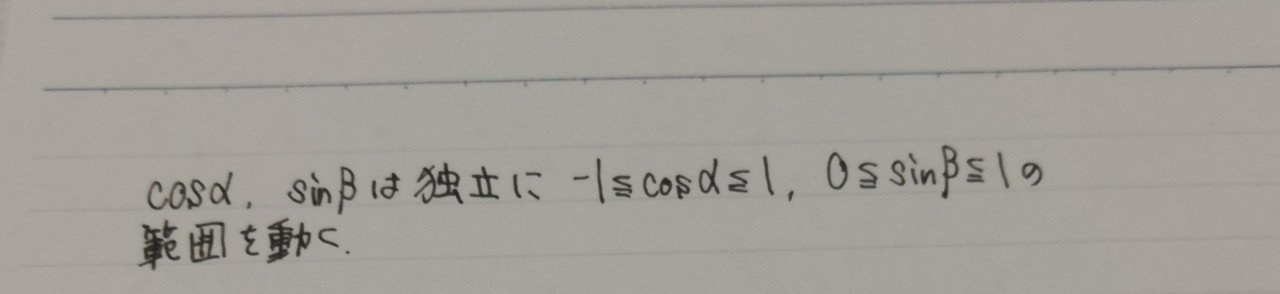
そして独立であるときの基本的なアプローチは、いくつかの文字を固定して、動くものを一つだけにすることです。
例えば、cosγを固定すると点Pの存在範囲は以下の線分となります。
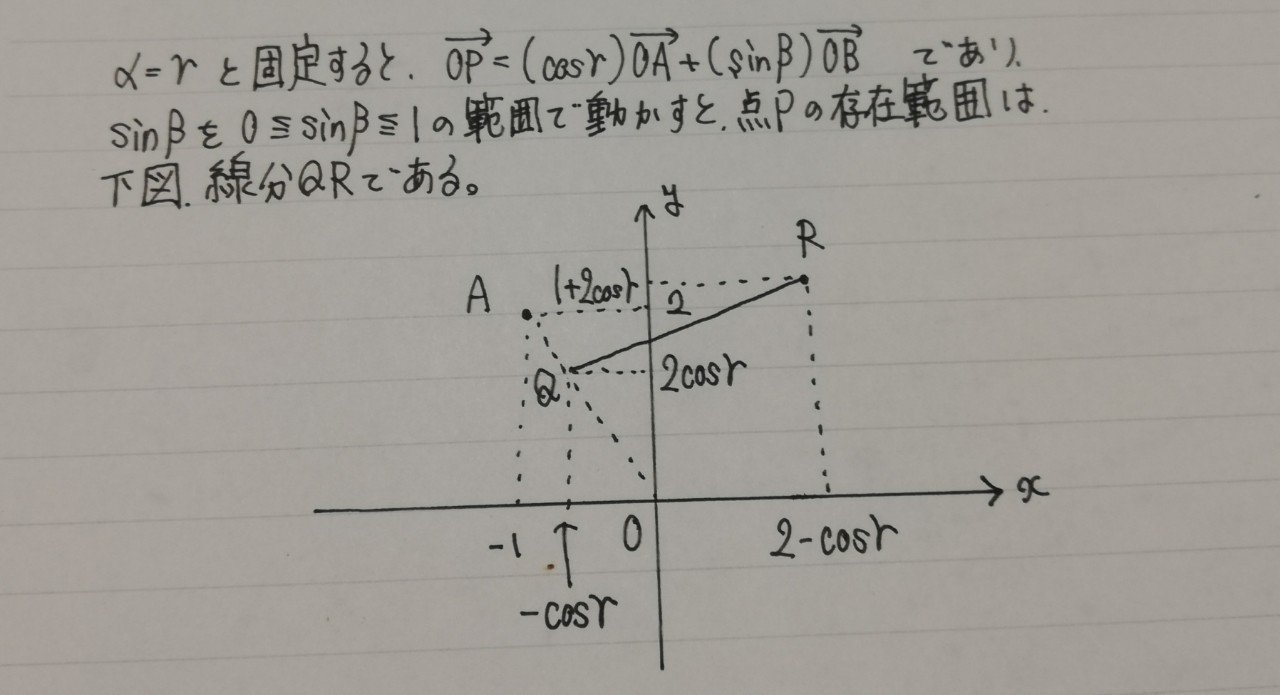
この状態で、今度はcosγを動かすと、それに伴って線分QRが動き、本来の点Pの存在範囲が以下のように求まります。
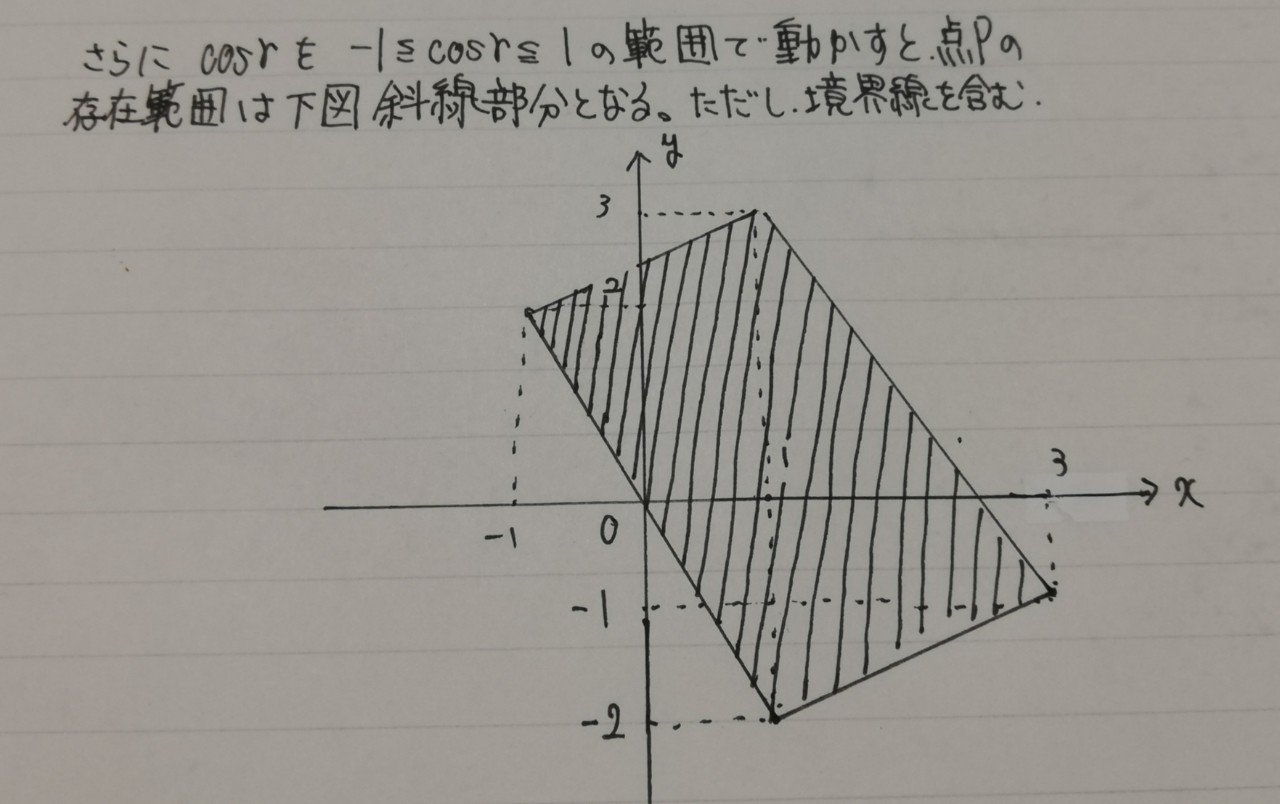
では、本問の別解(さすらい流とは言うのはおこがましいくらい有名)を紹介します。
大学入試界隈では逆像法と言われています。
平たく言うと、逆に考えると言うこと…
いやいや、これは適当過ぎましたね
具体的に言うと、
求める領域内の点(u,v)を取ってきたとき、この(u,v)を出力する上手い入力元の組(α,β)があるはずです。
そこで、入力元の組(α,β)が存在するための必要十分条件を考えるのが今から、紹介する逆像法です。
実際に答案を見ていきましょう。
出力先に注目すると、入力元があると記述することからスタートです。

さらに書き換えると

もっと書き換えると

ここが、ポイントで、α、βが存在するということは、cos,sinも当然存在します。
なので、次の書き換えが成立します。

さらに書き換えると

となって、求める領域を図示すると
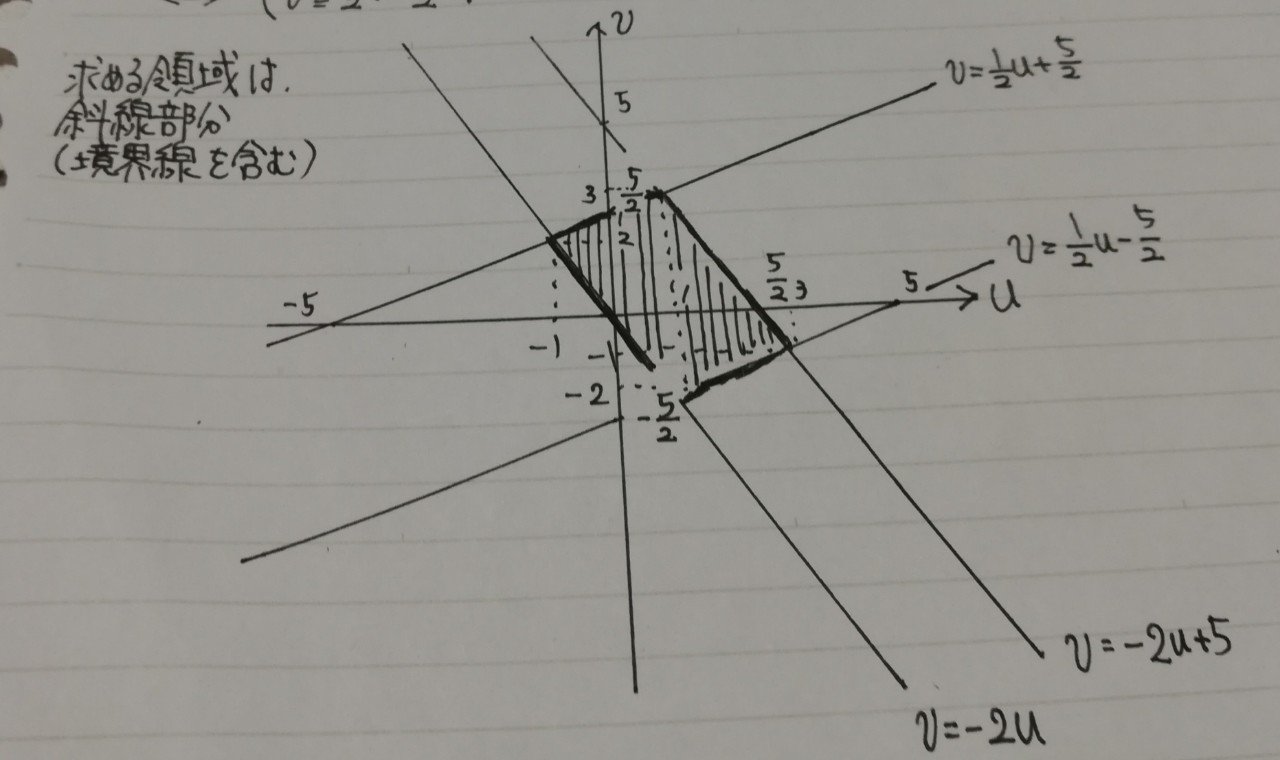
となります。
今日はここまで‼️
存在範囲は毛嫌いする人が多いですが、図を求められたときは、とても嬉しくなる問題です。めんどくさがらずにアタックしましょう。
そして次回の問題はこちら
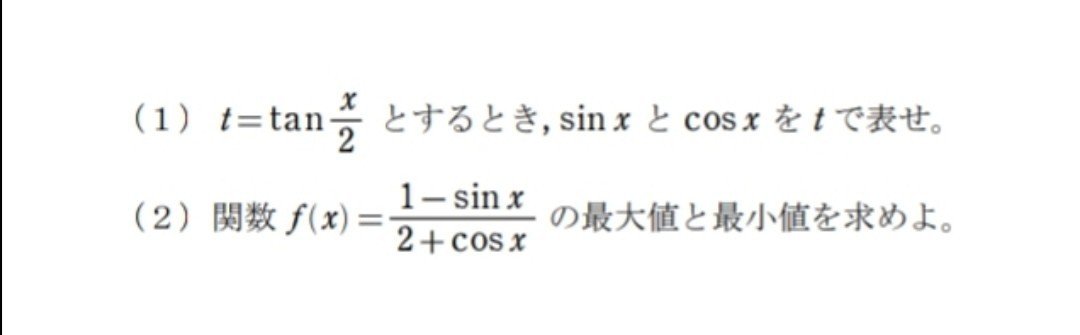
色々アプローチ方法がある一題ですね
では、次回をお楽しみに
良ければ👍、フォローをお願いします
