九州大学入試問題解説2022理系

2022年4月10日 17:14

新学期が始まりました。
今年度もがんばって投稿していきます。
今年の入試問題を少し目を通して見ると、なかなか面白い整数問題がいくつかありました。
一例としては、京都大学や東京工業大学です。京大の問題は実験では法則性を見抜くのが難しかったり、東工大の問題は解答の方向性がそもそも見えにくかったりしています。

今回このnoteで取り上げるのは九州大学の入試問題です。比較的難しい問題なのですが、解答自体は教科書の応用例題程度の知識で何とかなる教育的な問題となっています。
では、問題の紹介です。

問題もそこそこに早速解説に入っていきます。
まずは(1)から

考えている２数は隣り合っているので、この２数が互いに素であることを説明するのは容易です(教科書の傍用問題には確実にのっています)。なので、簡単な問題と思ってしまい、互いに素であることを示して終わってしまいそうです。ですが、それでは間違いです。というのも、本問で扱う２数は分数の形をしています。そのため、

そもそも整数なのか❓

ということに疑問を持ち、整数であることを示さなければなりません。そのことの証明も難しくありませんが、忘れやすく教育的な問題となっています。

続いて(2)に入ります。

168の倍数という、大きな数の倍数であることを示すことにぎょっとしますが、素因数分解をして、8,3,7の倍数であることを示せばいいことがわかります。それでも、難しそうに思えますが、本質は数を余りで分類することという、教科書に必ず載っていることだけです。
8の倍数であることを示すときに使った、a,a+1のいずれかは偶数は忘れやすいですが頻出事項なので使いこなせるようになりましょう。
(2)も解答を見ればとても教育的なものになっていることがわかりますね。

最後に(3)です。

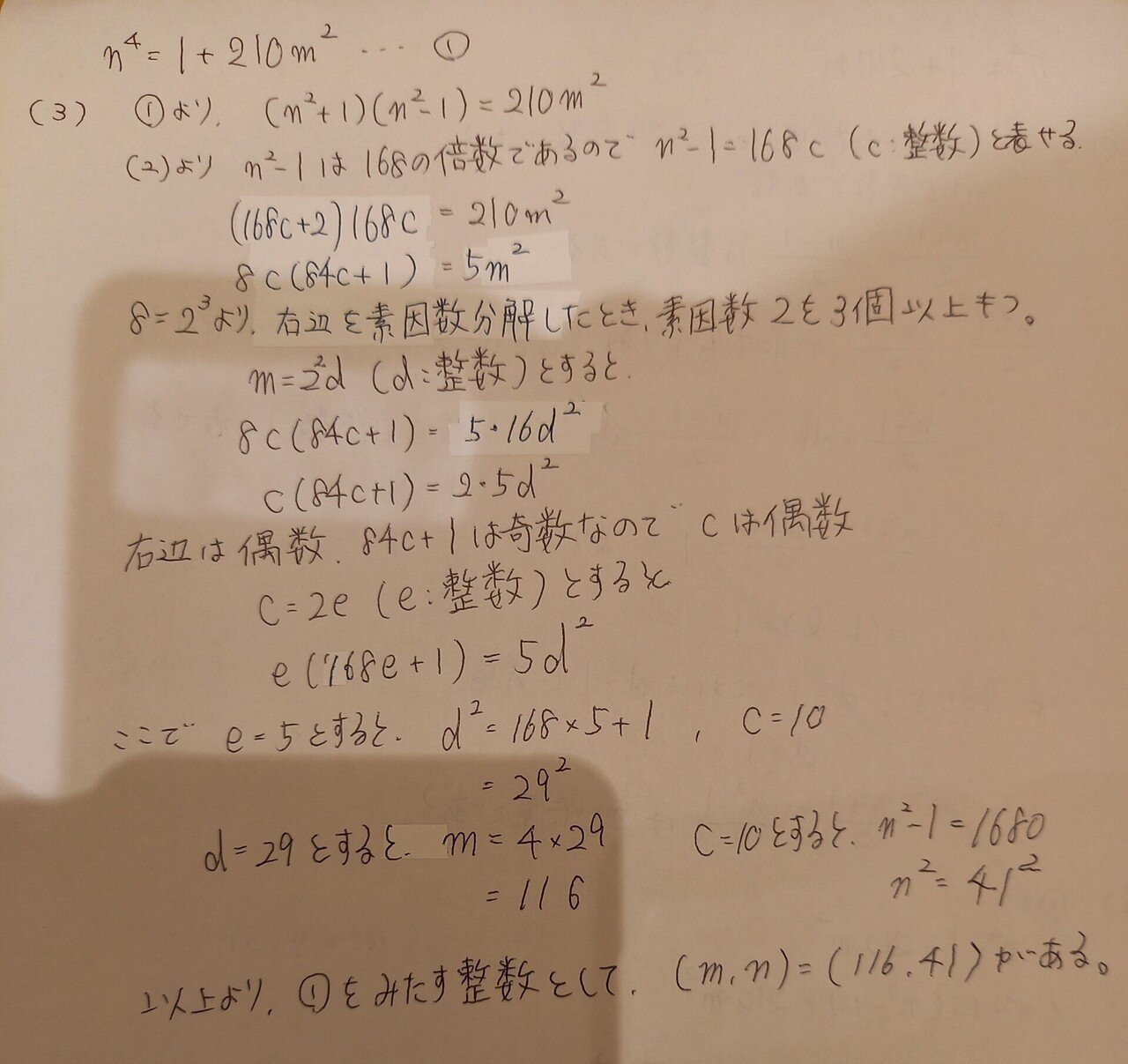
問題文から答えをすべて見つけるのではなく、一つ見つけるであることに注意しましょう。
ここまで来たのですから(2)を活用して、n^2-1=168cと設定するのが妥当でしょう。ここからも方針に戸惑いますが求めたいのはmとnです。nについては(2)でどのような数か把握できたので、mがどのような数かを理解することを考えましょう。すると8c(84c+1)=5m^2でm=4dと設定することが自然と見えてきます。
するとcがわかる　→　dがわかる
　　　　　　　　 →　m,nがわかる
という流れが出来上がります。
結果としてcの性質を理解し、決めうちをするとd,m,nが求まり、解の一つが求まります。

いかがだったでしょうか？(3)は少し難しかったですが、全体を通して見ると、難しい知識がなくても理解できる問題だったのではないかと思います。
今回はここまで。よければ👍️をお願いします。