数学力向上のヒント#2
久々の投稿
今回も数学力向上に繋がる問題を紹介していきます
数学力向上のヒント
有名不等式との関連性を考える
今回の問題はこちら

不等式を証明せよではなく、大小関係を調べさせるのが面白いところ。
ノーマルな解答はこちら
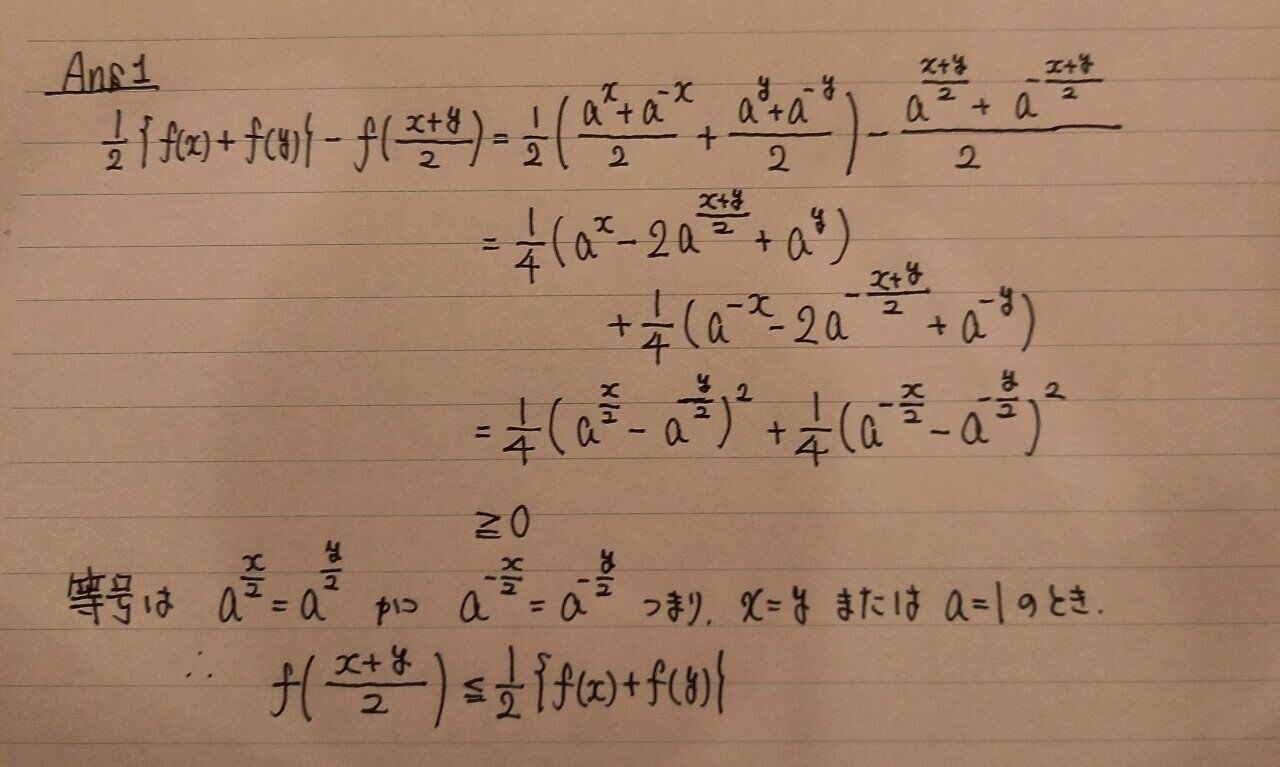
大小の当たりをつけて、差をとって、二乗の形を目指す。
オーソドックスな解答ですね。
では、この問題をどのように作ったのかを考えてみましょう。
背景にあるのは、次の不等式です。

聞きなれない不等式ですが、グラフの凸性に関しての不等式です。
では、これを既知として本問を解くと次のようになります。

なんと、微分して、数値を代入するだけで解決してしまいます‼️
要するに、出題者は下に凸な関数にイエンゼンの不等式を当てはめて、問題を作っていただけなのです‼️
あとは、差をとって、二乗の形を目指す方法で解けるかを確認するだけ(笑)
実は、こういった問題は探すとたくさんあって、例えば、相加平均相乗平均の不等式に当てはめただけとか、コーシーシュバルツに当てはめただけの問題があります。
なので、不等式の問題をみかけたら、有名不等式から導くことができないかなと考えてみましょう‼️
そうするだけで、解法の幅が広がります。
本日はここまで、ではまた次回
#ステイホーム
