大阪大学整数問題その2
今回も大阪大学整数問題の解説を進めていきたいと思います。
前回の記事はこちらから
今回扱うのはこの問題です。

この問いは大阪大学の問いでは易しい問題であると思われます。というのも、整数と無理数が関係する事実は次に載せるもの程度しかなく、教科書にも必ず載っているからです。

では、この事実を用いて、整数の組を求めてみましょう。
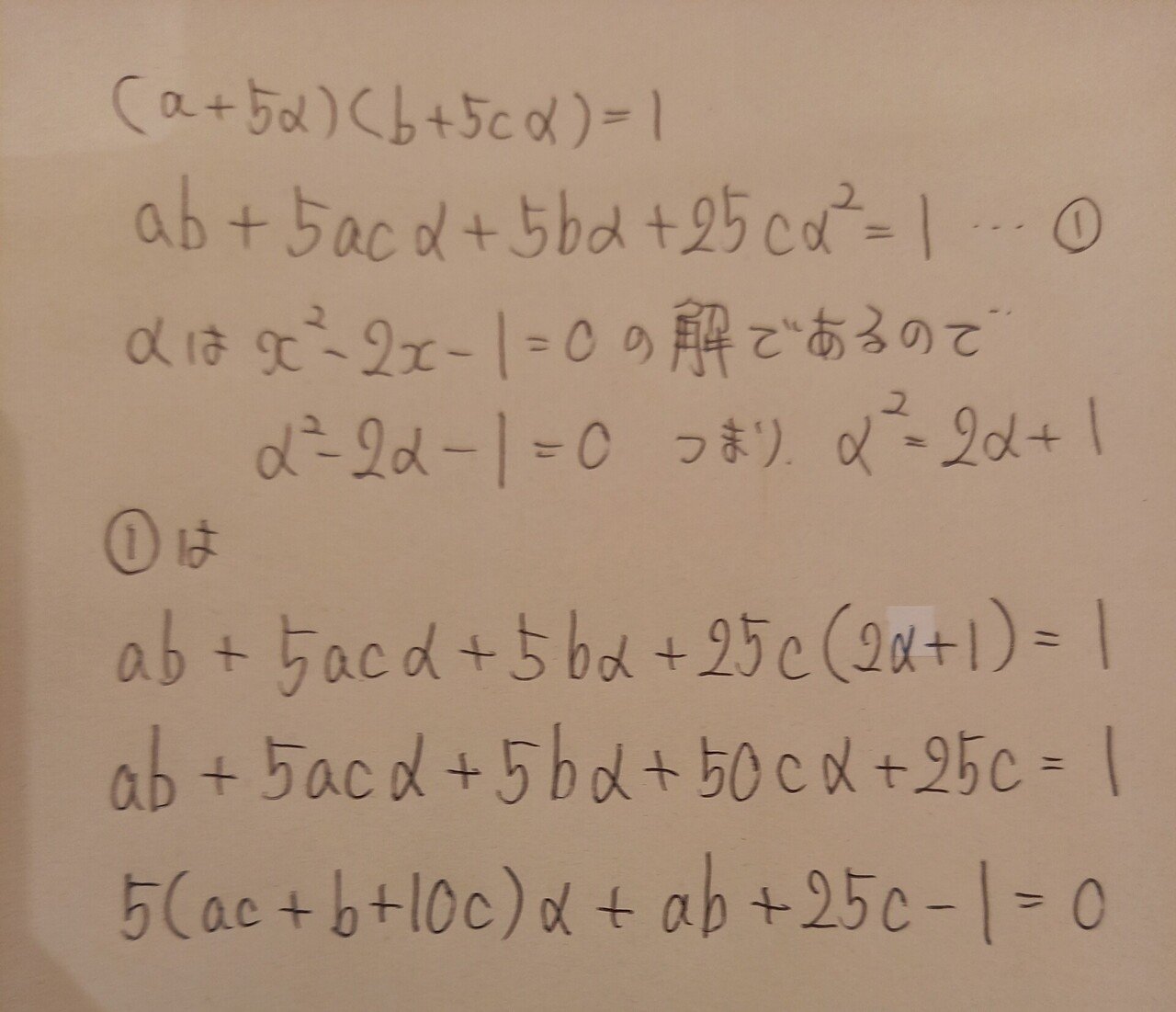
上の事実の形に持っていくためにα^2に次数下げを用いてαの1次式で表したのがよくあるテクニック。案外使いこなせない人が多いので、入試に向けてできるようになっていきましょう。
上の事実の形に持っていけたので、αの係数、定数項の比較に入っていきます。

ただ、比較するに当たって、係数が有理数であることと、αが無理数だあることの確認を忘れてはいけません。
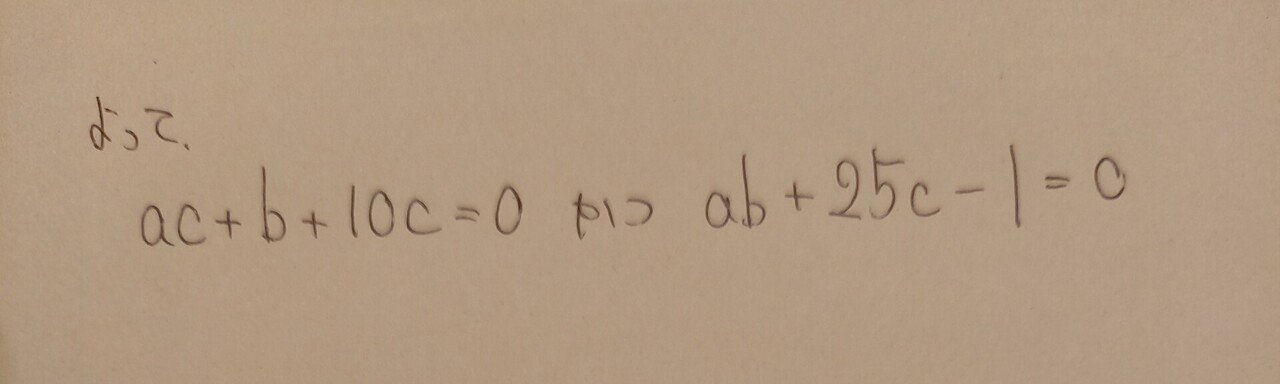
ここからは、a.b.cの連立方程式を解いていくことになります。ここで気付いておいてほしいこととして、未知数が3つに対して式が2つであることから、どこかでa.b.cが整数であることを用いるということです。では、解いていってみましょう。
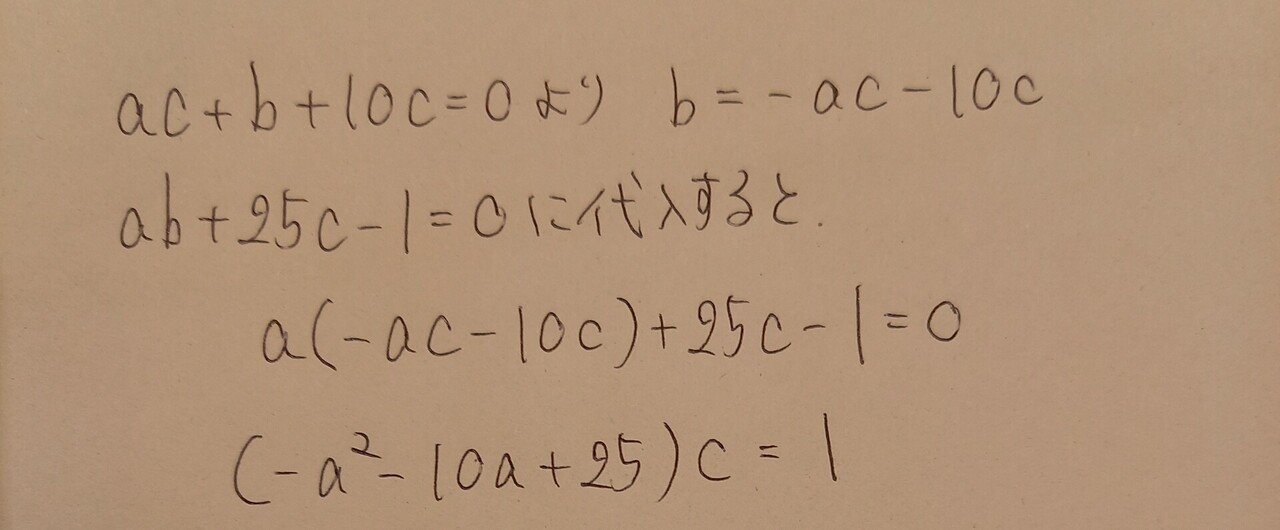
連立方程式は消去しやすいものを消去するのが鉄則(予備校界で有名な安田先生の著書にも書いてありました。)
本問ではbを消去していくのがわかりやすくて、上記のように整数✖️整数=1の形になります。ここまでくるとcを特定するのは簡単で1or-1の2つしかありません。
以下、丁寧に場合わけをしていくと、

とこのようにa.b.cの組を求めることができます。
いかがだったでしょうか?有理数と無理数の間にある基本的な事柄を押さえておくだけで簡単に解けてしまいましたね。
本問の類題としてあげられるのは以下の問題があります。

京都大学で出題された一題です。ぜひ、挑戦をしてみてください‼️
今回はこれにて終了とします。よかったら👍️をお願いします。
