
【中学受験:算数】論理パズル「数当て」の解き方 (ここはこれは無いよね理論)
問題文の解釈
今日は「数当て」という論理パズルの解き方です。
出題は天才脳ドリル(上級)より引用です。

ルール
① はこが4つあります。はこの中に数字が入っています。
A~Cの3人がはこの中の数当てをしています。
② 〇は、正確に当てることができた数字の数を表しています。
③ △は、はこをまちがえた数字の数を表しています。
④ はこの中には同じ数字は入りません。
⑤ 4つのはこの中に入っている数字を求めなさい。
まず、この問題を理解するのが難しいですね。
この問題文は、少し言葉足らずなところがあるので、補足しましょう。
(この手の言葉足らずは、言葉が足らないと怒るよりも、謎解きゲームを解くと思いましょう)
② 〇は、正確に当てることができた数字の数を表しています。
③ △は、はこをまちがえた数字の数を表しています。
まず、「正確に当てる」とはどういうことか。
③には「はこをまちがえた」とあるので、②は「箱の場所も当たっていて、〇〇も当たっている」という事でしょう。
それでは、〇〇はというと数字でしょうね。
そうすると、②、③の文を正確に理解するとこうなります。
② 〇は、箱の場所も含めて当てるができた数字の数を表しています。
③ △は、はこの場所は間違えたが、別の場所のはこには入っている数字の数を表しています。
そうすると、もう一つカテゴリーを作りたくなりませんか。
「そもそもはこに入っていない数字の数」、これを×とする。
このカテゴリーを入れることで、MECE(ミーシー)になります。
MECEとは、日本語にすると「モレなく、ダブりなく」という意味で、論理パズルを解くときに大切な概念です。
そうすると、問題の表も以下のように書き換えられます。
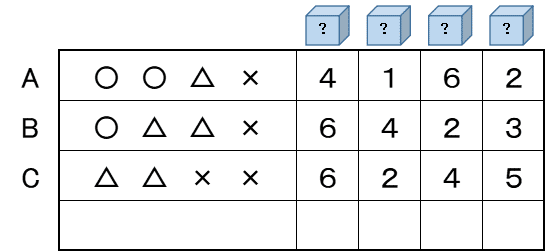
問題の理解
それでは問題を理解していきましょう。
ここで使われている数字は1,2,3,4,5,6の6種。
はこに入っているのはこのうち4つの数字で、2つは落選です。
2,4,6はABC全員が選んでいて。1,3,5はABCがそれぞれ1つずつ選んでいます。

さて、ここで、ABは×1つで、Cだけが×2つです。
そうすると、落選する数字のうち一つは分かりますね。1,3,5の内でCに選ばれた5です。もう一つの落選は、全員が選んだ数字の中にありますが、2,4,6のどれかはまだわかりません。

ここはこれは無いよね理論
さて、これまでの論理パズルでは、「ここはこれしか無いよね理論」と言って、答えが分かる(一つに決まる)場所から埋めていく、ことをしました。
ただ、この問題ではそのような場所がありません。
そこで、「ここはこれは無いよね」という形で、消去法により可能性を絞っていく手法を使いましょう。
ここではAに着目すると、箱が4個ある中で、数字と場所の両方が正しい〇が2か所あるので、〇の付け方のパターンは6個です。
この6パターンについて、これは無いよね(矛盾するよね)ということを検証しましょう。

パターン1

パターン1は上記の状況なので、?の二つを考えましょう。
この点、パターン1はさらに2つに分岐します。
つまり、2,4,6の中から1つは落選なので、2の落選のパターン(パターン1-1)と、6の落選のパターン(1-2)に分かれます。
パターン1-1
2が落選なので、4,6が当選です。4はすでに当選しているので、6を?に入れますが、「箱う」に入れると、Aの〇が3つになってしまうので、「箱え」が6になります。
「箱う」には、3が入ります。(そもそも、5は、全パターンで落選ですからね)

さて、そうすると、Bは矛盾がないでしょうか?
これだとBには〇が1つも無いはずなので、矛盾します。従ってパターン1-1は没です。
パターン1-2
6が落選なので、2,4が当選です。4はすでに当選しているので、2を?に入れますが、「箱え」に入れると、Aの〇が3つになってしまうので、「箱う」が2になります。
「箱え」には、3が入ります。

そうすると、Bは〇が2つになって矛盾します。従ってパターン1-2は没で、パターン1は全部没です。
(要は、これを矛盾の無いパターンが見つかるまで続けるだけです。)
パターン2

パターン2は上記の状況なので、?の二つを考えましょう。
まず、2,4,6の中から1つは落選なので、2の落選が確定です。あとは、1,3は当確なので、?には1、3が入りますが、「箱い」に1を入れると〇が3つになってしまうので、「箱い」に3、「箱え」に1で確定です。

そうすると、Bは〇が0になって矛盾します。従ってパターン2は没です。
パターン3

パターン3はパターン2に似ていますね。
まず、2,4,6の中から1つは落選なので、6の落選が確定です。あとは、パターン2と同じく「箱い」に3、「箱え」に1で確定です。

そうすると、Bは〇が0になって矛盾します。従ってパターン2は没です。
パターン4

パターン4は上記の状況なので、?の二つを考えましょう。
この点、パターン1と同じく、2つに分岐します。
つまり、2,4,6の中から1つは落選なので、2の落選のパターン(パターン4-1)と、4の落選のパターン(4-2)に分かれます。
パターン4-1
2が落選なので、4,6が当選です。6はすでに当選しているので、4を?に入れますが、「箱あ」に入ると、Aの〇が3つになってしまうので、「箱え」が4になります。
「箱あ」には、3が入ります。

そうすると、Bは〇が0になって矛盾します。従ってパターン4-1は没です。
パターン4-2
4が落選なので、2,6が当選です。6はすでに当選しているので、2を?に入れますが、「箱え」に入ると、Aの〇が3つになってしまうので、「箱あ」が2になります。
「箱え」には、3が入ります。

そうするとBは、〇が1つ、△が2つ、×が1つと完全に矛盾がありません。
Cを見てみると、△が2つ、×が2つと、こちらも完全に矛盾がありません。
従って、これが正解になります。

まとめ
いかがでしたでしょうか。
このように、「ここはこれしか無い」と一発で分からない場合には、「ここはこれは無い」と選択肢を絞って、各パターンを一つずつ調べていくという手法で解きます。(力技ですね)
ここで、なるべく少ないパターン設定にできるように、選択肢を絞っておくことが重要です。
この問題、もっとスマートな解き方がある気もするのですが、私には思いつきませんでした。
もしわかる方がいれば、コメントで教えていただければありがたいです。
