【中学受験：算数】論理パズル「道をつくる　Ⅱ」の解き方　（ここはこれしか無いよね理論）

論理パズルの「道をつくる」の別パターンの問題です。

ルールは以下の通り。
１．スタートからゴールまでの道順を記入
２．同じマスを2回以上通れない
３．進める方向は、たてと横だけで、ななめには進めない
４．数字は、その列のマスのうち、道が通るマスの数を表す

この問題も、ここはこれしか無いというところを見つけましょう。
じゃあ、どのような場所が「これしか無い場所か」というと、基本的になるべく極端な場所が「これしか無い」と決まりやすいです。

じゃあ、この問題において、極端な場所(条件)となるのはどんな場所か。ここは、1回しか通れない「1」か、全部のマスを通らないといけない「8」が極端でありそうです。この問題では8がないので「１」を見ていきましょう。

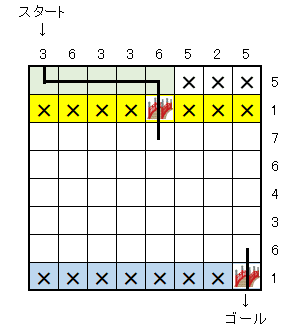
1は2行(黄色と青)がありますが、簡単なのは下の青いほうです。
ゴールは右下なので、右下のマスを通るしかない。しかも、1なので、横には行けないから、上に行くしかありません。
イメージとしては、１というのは、「両サイドを繋ぐ橋を1か所だけ置ける」という感じです。

そして、ほかのマスは通ることができないので、×と書いておきましょう。

次に、上の黄色いほう。
こちらも１なので、両サイドを繋ぐ橋を1か所だけ置けます。どこに置きますか？
ヒントとしては、黄色の上の行がスタート行で、スタートのマスから5マス分通ります。ということは、黄色行における橋は1か所だけなので、スタートから5マス分を通って、黄色行の橋を使って下に行くしかありません。（緑部分）
なぜなら、1回黄色行より下に行ってしまうと、もう上の行には戻れませんからね。
そして、通らないところは×を書いておきましょう。

それでは、「1，8」に次いで極端な数字の「2，7」を見ていきましょう。
まずは２から。

２の特徴は、１と同様「１度渡ったら戻れない」ということです。
下の図を見てください。もし、２の時に１マスの橋を渡ってしまうと、2にするために、もう一度その列に戻らないといけないのですが、そうするともう反対側に行くことができなくなります。

したがって、「2の時には1マスで反対側に行って、また戻る」ということができないので、以下の2通りの通り方しかありません。

上記2通りのどちらにせよ、一度渡ったら戻ることができないので、青の列を渡る前に、一番右の緑列の５マスを全て通らないといけません。

したがって、ここの通り方はこれしかありません。

さて、そうすると、ピンクマスから、上と下どちらに行くでしょうか。
まだ、それは今の条件では確定できないので、次の条件を見ていきましょう。
7の行です。

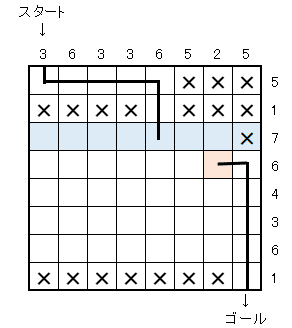
７の特徴は、通らないマスが１つあることなのですが、実は先ほどの右端5の列の確定によって、通らない１マスが確定していますので、それ以外の全てのマスを通ることが確定しています。
（ちなみに私は、通ることは確定しているけど、通り方は確定していないマスに〇を薄く書いています。）

実は、これを見るとピンクのマスから上と下のどちらに行くかが確定しています。
ポイントは、ピンクの一つ上の緑のマス。
この緑のマスは通ることは確定していますが、このマスから上と右に行けません。したがって、このマスを通るには、このマスの左と下のマスを通るしかないのです（赤いコース）。
そうすると、2の列のほかのマスは通れないので×です。

次に、7の行の一番右の緑マスを見てみますと、通ることは確定していますが、上と左に行けないので、右と下のコースで確定です（赤いコース）

それでは、次に極端な「3，6」を見ていきましょう。
どの３、６を見るかですが、まず「すでに規定数のマスを通っている行列があれば、それで確定」ですよね。
この点、１番左列がすでに3マス通ってますので、それ以外のマスは×です。かつ、緑マスからは右に行くしかないので、ここも確定です。

次ですが、ヒントが多い端っこで「3，6」になっている行列を見ていきましょう。
そうすると、×によって端っこのマスになったオレンジを含む行列は、端っこであることに加え6になっているので、そこに注目です。

この6の行も列も、すでに２つの×を含んでいるので、残りの空のマスはすべて通りますので薄く〇をつけましょう。
そして、オレンジマスは、端っこで上と右しか行けないので、赤いコースで確定です。

次は、6の列横の3の列の２列です。
ここは、すでに通るマスが3マス確定しているので、それ以外が×になります。
そうすると、自ずと通るルートが確定しますね。（赤ルート）

次に、以下の6，4の行については、×の数がそろっています。よって、空のマスは通ることになるので〇のマスになります。

それでは、ヒントも増えているので、最後の空欄も〇×をつけてみましょう。
６の列はすでに通るマスが6個あるので空のマスは×、5の列は〇が4個なので空のマスは〇です。

そうしたら、〇のマスを全て通るように、線を引きましょう。

いかがでしたでしょうか。
この手の問題は、後半になるほどヒントが増えて解きやすくなっていきます。これはナンプレなどもそうですが、最初どこから手を付けるかがポイントになります。

その際に思い出していただきたいのが、「ここはこれしか無いよね」という場所を見つけるのが大切で、「極端な場所」ほど、「これしか無い」場所になりやすい、ということです。

この問題では、１と２が「一度渡ったら戻れない」という点で、「ここはこれしか無い」の法則が使える場所という形で、この法則を使えるのです。

「天才脳ドリル　仮説思考」という問題集が、この手の問題の練習にとても良いです。入門・初級・中級・上級とありますが、上級は大人でも慣れていなければ、苦戦すると思います。この手の論理パズルは「ここはこれしか無い」理論で解けるものが多いので、ぜひチャレンジしてみてください。

ちなみに、同じような問題の「道をつくる」についても、解き方を書いているので、ご覧いただければありがたいです。