Besiegeで学ぶ機構学#3の振り返り。

　閲覧ありがとうございます。「Besiegeで学ぶ機構学#3、リンク機構の基礎（Youtube、niconico）」を振り返るnoteです。

導入

ここで挙げた３つの機構「歯車機構」「カム機構」「リンク機構」について、すごく雑ですが、

歯車機構…回転速度を変換する機構
カム機構...運動の方向を変える機構
リンク機構...入力を異なる動作に変換する機構

と言えます。もちろん例外は多々（歯車におけるラック＆ピニオンとか）あります。
私がリンク機構に魅力を感じる理由は、これらの中で機構の最小単位が一番単純なのにも関わらず、それをたくさん用意して組み合わせることで複雑な動作を実現できる点にあります。
とはいえ、この動画シリーズで最初にリンク機構を扱うのは、他の機構を考える際にもリンク機構は分かった上でやらないとわけわからんことになるからです。この辺の話は次回ちょっと触れると思います。

OP

うんこ。

リンク機構とは？

このシーンで言った「この定義に当てはまらないもの」について触れておきましょう。
機械学会による「リンク機構」の定義はこの通りなのですが、同時に環状になっていない機素が対偶でつながったものも「リンク機構」の一部だと解釈されることもあります。環状になったものを「閉リンク」「クローズドループ構造」、環状になっていないものを「開リンク」「オープンループ構造」と呼びます。　
あまり「環状」に重点を置かずに考えましょう。

リンク機構の運動

てこクランク機構は閉リンクのリンク機構の中で一番単純なものじゃないかなと思います（異論は認める）。実用されているものでは、足踏みミシンなんかがわかりやすいかもしれません。

この↑動画では、リズミカルな足踏みによる揺動運動がでっかい車を回し、それをベルト＆プーリーでミシンに伝えています。こっちの動画の方が機構は見やすいかも。ちょっと長いけど。
それにしても、昔のミシンってどれもかっこいいですよね。今の白とか、淡い色とかのやつはあんまり好きじゃありません。清潔感を重視してるんでしょうか。
話が逸れました。この足踏みミシンはてこクランクのうち、てこの方に足を置いて動かしています。つまり動力源がクランクではなく、てこにあるのです。よって、足踏みミシンのてこクランク機構について、駆動リンクはてこ側と言えます。駆動リンクが常にクランクだと思わないようにしてください。

両てこ機構、両クランク機構においても、この考え方は同様です。今回の動画でこれらの説明をしているときは、常に固定リンクの左端に動力がついているという前提で話しています。
一般的に、動力は固定リンクの端のどちらかにつくものであり、今回の例のようにモーターやエンジンをブンブン振ったりはしません。どれが駆動リンクかよくわからなくなる問題はBesiege等、ゲームにだけ存在する問題だと思ってもらって結構です。

固定するリンク、というか固定する機素を変えると機構の運動の様子は大きく変わります。地面に足をついてバーベルを持ち上げる人と懸垂をする人で体の動きは同じでも、見た目は全然違うみたいなものですね。
差動機構の一端を手で止めるようなもの、と言えばわかる人にはわかるでしょう。

リンクを増やしたりしてみる

トラス。割と誤解を招きやすく、立場によって使い方が変わってくる言葉です。

トラス構造とは本来、「回転対偶で接続されてるけど動かない連鎖」のことを指します。三角がたくさん繋がってる奴ですが、大事なのは三角と言うことよりも「回転対偶でつながっていること」です。回転対偶でつながっておらず、しっかりくっついて回らないようになっている構造を「ラーメン構造」と言います。

とはいえ、そのへんのトラス橋の三角の頂点がぐるぐる回るようになっているわけではありません。ではなぜ、あれがトラス橋と呼ばれているのか。
それは、トラス橋を設計する際、一旦回転対偶でつながっているものとして計算しているからです。
（しっかり固定された）トラス橋のそれぞれの部材には、大きく分けて三つの力がかかります。引っ張る力、圧縮する力、そして曲げる力です。ここで接続をすべて回転対偶によるものだと仮定すると、部材にかかる力は全て引っ張る力と圧縮する力の二つになります。すると計算が比較的楽に行えるようになり、かつしっかり固定されていると置いて計算した時とほとんど同じ結果が得られるのです。この辺は「材料力学」の分野ですね。
実際には、橋の部材同士の接続はボルトをいっぱい刺してぎっちり行います。すべての接続に回転対偶を作るよりも、よっぽど安いからです。

というわけで、バラストの間をブレースで三角につないだような構造は正確にはトラス構造とは言えません。あえていうなら、トラス状、くらいが限界でしょうかね。まあトラス状を略してトラスって言ってると思いましょう。
ちなみに、トラス橋が地面と接するところにはクソでかヒンジがあります。気温の変化による変形を受け止めてくれたりします。けなげな奴ですね。

リンク機構の自由度を求める

グルーブラーの式、実は最初に発表された式が完全じゃなかったりなんだりしたせいで、名前がいっぱいあります。英語のWikiの名前は「Chebychev–Grübler–Kutzbach criterion」です。長い。

この式で計算できない機構に「過拘束機構(Overconstrained mechanism)」と言うのがあります。まあ、だいたいはすっごい特殊な機構なので、自分で計算して合わない時はほとんどの場合、計算ミスだと思います。

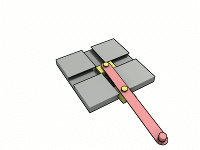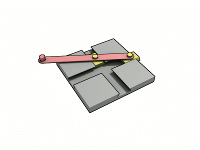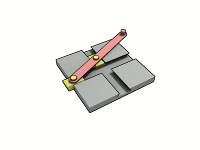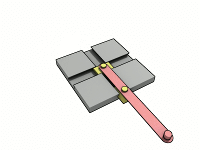
一番単純そうなやつでこれ↑ですからね。

ポースリエの解説は次回。

締め

エンディング、なんかよくない？
でもなんか「完」感あるよね。終わりません。

次回はちょっと楽しいと思います。私の編集カロリーは高いけど。

というわけで、今回もご視聴・閲覧ありがとうございました。細かいところの編集ミスが目立ちますね。フェード忘れとかフェードインの遅れとか。まあこんなもんでしょう。