
中二病でも「連続体仮説」と「不完全性定理」を理解したい!③
前回:https://note.com/ktkusayama/n/nfd6295a7bb2a
だいぶ間が空いてしまった。というか忘れていた。なので加筆。
前回は無限集合のレベルみたいな概念である「濃度」について触れた。そこで、自然数の集合に一対一対応がつくれる集合は、すべて濃度が一緒ということにしてその濃度を「ℵ_0(アレフ・ゼロ)」というカッチョイイ名前で呼ぶことに決めたのだった。有理数やガウス整数、代数的数なんていう集合まで全部濃度はℵ_0なんだという。
じゃあ全部ℵ_0なんじゃね?
チッチッチッ(人差し指を横に振る)
実は実数の濃度は、ℵ_0よりも大きいことが分かっている。
ではこれを証明した「カントールの対角線論法」について、ざっくりと説明していこう。
実数全部に番号振れるマン、参上!
カントールの対角線論法について、形式的に厳密な証明はしかるべき書籍をあたってもらうとして、雰囲気だけ簡単に理解していこう。
濃度がℵ_0に該当する集合は「その要素が自然数で番号付けできるもの」だった。なのでここで、架空の「実数全部に番号振れるマン」というものを登場させてみよう。もしコイツのいうことが本当なら実数の濃度はℵ_0だし、矛盾があったらℵ_0ではないことになる。
実数全部に番号振れるマンは「〇〇という数はどこにありますか?」と聞くと、当然じぶんで実数全部に番号振れるマンと名乗っているのだから「△番目にあるぜ!」と答えてくれるはずだ。
実数全部に番号振れるマンに実数全部に番号振ってもらいましょう
実数全部に番号振れるマンがどんな規則にそって番号付けをしているかはわからないので、とりあえずちょっと書き出してもらおう。
といっても実数はあまりにも多いので、0から1までの間の数だけで大丈夫です。実数全部に番号振れるマンさん、よろしくお願いいたします。
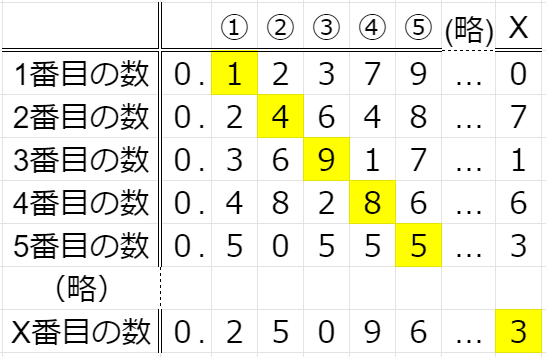
こんな感じらしいです。ありがとうございます。
ここである操作を行う。それはどんな操作かというと、
①1番目の数の小数第1位、2番目の数の小数第2位を順番に足していって新しい数を作る
上の図だと、黄色で示したところを足していって「0.14985…」という数を作る。
②小数点以下の数について、数字をすべて+1してずらし、新しい数を作る(1→2→3→4→5→6→7→8→9→0→…)
この規則は実は何でもいい。たとえば偶数を適当な奇数に、奇数なら適当な偶数に置き換えるとかでもいい。とにかく「違う数字になる」ような規則で新しい数を作る。
たとえばさっき作った「0.14985…」という数は「0.25096…」という数になる。
カントールに論破してもらいましょう
実はさっき作った「0.25096…」という数は実数全部に番号振れるマン(以下:実マン)には作れない数なのである。
俺「すいません、この新しい「0.25096…」という数、どこにあります?」
実マン「あ~それね、たぶんX番目にありますよ」
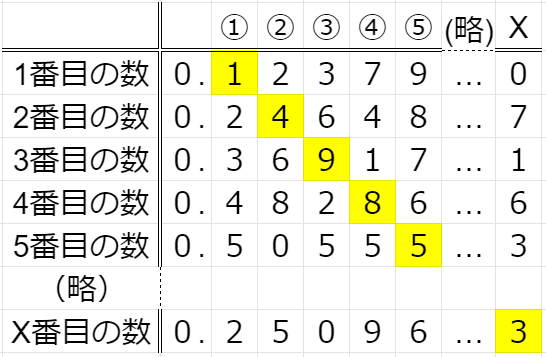
もし実マンがこのように答えたとしよう。確かにX番目には0.25096…っぽい数があるのだが、この数の小数第X位は「3」で、俺が尋ねた数は第X位が一つズレた4なのだ。これは俺が探している数とは違う。
「いや、2679458235番目にありました!今度はあってるはず!」などと言ったとしても、その数は第2679458235位が違う。実マンが「〇番目にあるはずです!」と言っても、それは必ず第〇位が俺の言っている数と違うのだ。
こんな感じでいたちごっこになってしまい、実マンがこの数に番号を振れていなかったことが判明。
ハイ論破~~wwww
というのが、カントールの対角線論法なのである。
で?
論破したはいいものの、ここから何が分かるのだろう?
さっき作り出した「0.25096…」という数は0から1の間に存在しているにも関わらず、それは実数全部に番号振れるマンには作れない数だった。つまり上の対応表からあふれた数なのである。
それは「実数全部に番号振れるマン」が存在しないこと=どんな番号規則を作っても自然数と一対一対応させることができない実数が作り出せるということであり、実数の濃度は自然数よりも多いということなのだ。
ということで、自然数の濃度より大きい濃度があることが分かった。これを「ℵ_1(アレフ・ワン)」と名付けよう。う~んカッコいい!
あ、そういえばこれはあくまで0から1の間の話なんだった。でも大丈夫。0
~1を-π/2~π/2の区間に対応させてtanで飛ばすとかやれば実数全体に全単射がつくれるよ。まあこのへんは込み入った話になるので割愛。
とにかく数直線の一部を切り取るだけでも、自然数よりデケえクラスの無限があるということなのだ。
連続体仮説の主張とは
では本題。ℵ_0よりもℵ_1が大きいことがわかり、カントールはこう考えた。
「濃度がℵ_0より大きくてℵ_1より小さい無限集合ってあるのかな?」
たしかに当然の疑問である。
そして「連続体仮説」とは、「このような中間にあたる無限集合は存在しない」という仮説である。
対角線論法がトンチみたいなものだったので、こいつもなんか、うまいこと証明できそうな気がする。
ところがどっこいコイツは「現代の数学の枠組みでは証明も反証も不可能であることが証明されている」というのだ!
次回は連続体仮説についてさらに深く掘り下げていこう。
