
27.03 三角関数(準備③角の拡張と象限)
導入
度数法において、測れる角度の範囲は 0度 から 360度 まででしたね。でも多角形の内角の和を考えると 三角形は 180度、四角形は 360度 でしたが、五角形は 540度、六角形は 720度 と360度を優に超えます。でも内角の和なので何の問題もなく受け入れたと思います。
角の拡張というのは 0度 から 360度 まで の範囲に収まらなくても意味を持たせようというものです。720度なら2回転分だろうと考えた人もいるかと思いますが、それを一般化しようというのが話の中心です。
明石家さんまさんが昔、自分の父の話を笑いのネタにしていました。
おやじが「高文の人生は380度変わった」と言うてね
「ボクの人生、一回転して20度しか変わってへんのかい」
さんまさんは角の拡張を理解してたのですね。
さてここで思い出してください。三角関数では角を弧度(ラジアン)で考えるという約束でしたね。ここからは $${0 \leqq \theta \leqq 2\pi}$$ を超える範囲に意味を持たせ、考えられる角の範囲を実数全体に拡げていきます。
角の拡張
角$${\theta}$$の大きさを回転と捉えると $${2\pi}$$ を超えても考えることができます。例えば、$${3\pi}$$ という角は1回転半と考えます。フィギュアスケートでの3回転半ジャンプは $${7\pi}$$ジャンプ ということになります。
さらに角を拡張します。
回転にも右回り、左回りがあるので、数学では左回りを正の向き、右回りを負の向きとします。このように考えた角を一般角といい、角の大きさが実数全体に拡がります。
※ 左回り・・・進行方向左手側に極(中心)がある, 右回り・・・時計回り(※2)
知識の整理
平面上に基準点Oと、これを端点とする半直線OXを取ります。次にOを端点とする半直線OAをOを中心として回転させます。

用語を書き入れましたが暗記をする必要はありません。この用語を使うのは最初のうちだけです。正の向き、負の向きの約束だけは覚えてください。
左回りを正の向きとするのは数学での慣習ですが、陸上のトラックを走るのも、野球の進塁も左回りなので覚えやすいと思います。
確認問題1 次の角に対する動径を図示せよ。
(1) $${\dfrac{\:2\pi\:}{3}}$$ (2) $${-\dfrac{\:\pi\:}{2}}$$ (3) $${-\dfrac{\:4\pi\:}{3}}$$ (4) $${\dfrac{\:7\pi\:}{2}}$$
確認問題2 動径OAの表す角θを答えよ。ただし、θは実数とする。
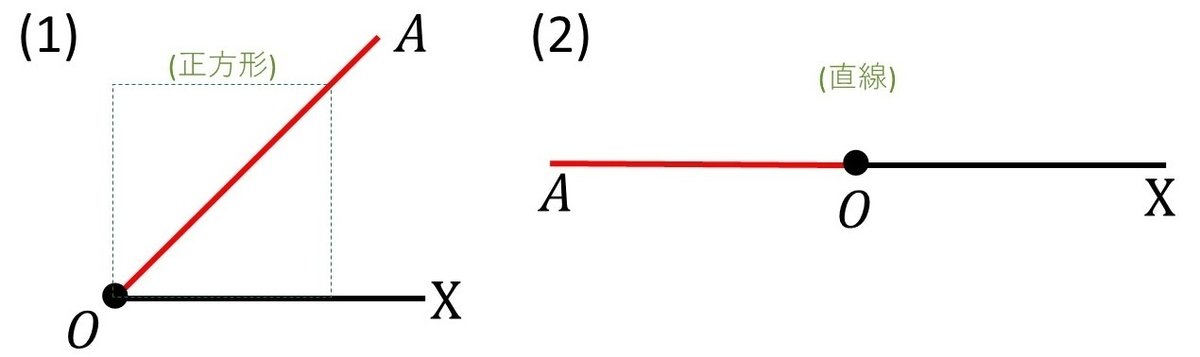
確認問題1の答え

確認問題2の答え (1) $${\theta=\dfrac{\:\pi\:}{4}+2\pi n \:\:(n\in \mathbb{Z})}$$ (2) $${\theta=\pi+2\pi n \:\:(n\in \mathbb{Z})}$$
※ $${\mathbb{Z}}$$ は整数を表す記号
マガジンには高校数学Ⅱの指数と対数、微分と積分も掲載予定です。応援してくれるとうれしいです。
安心して創作活動が続けられるよう応援してくださると助かります。いただいたチップは書籍もしくは文具の購入に当てたいと思います。

