33.02 複素平面（複素数を点とみる）

複素平面の最初の話をします。実数を直線上の点と捉えたように、複素数を平面上の点と捉えます。ではそれをどう考えるか･･･
前回の内容を踏まえて話を展開します。

複素平面

実数を大小の順に横一列に並べると直線が得られます。これが数直線と呼ばれるもので、実数が捉えやすくなりました。複素数も似たことができないかと考え、そして得られたものが複素平面と呼ばれるものです。

最初に考えた人はノルウェーの数学者 ウェッセルで、1799年に発表されていますが注目されなかったようです。1806年フランスの数学者 アルガンによって再発見され、その図は現在も用いられています。さらに1831年、ドイツの数学者 ガウスによって三度目の発見がなされました(※1)。三番目ですが複素平面はガウスの名で知られています。そのため複素平面はガウス平面とも呼ばれます。アルガン図という呼び名は非常に稀です。

複素数を平面で捉えることによって何がうれしいかというと、複素数を変数とする関数の研究が進めやすくなることです。実数を変数とする関数がグラフを通して考えやすいのと同じです。その結果、代数学の基本定理が証明され、電磁気学では欠かせない道具になり、量子力学のシュレーディンガー方程式を得ました。複素数を変数とする解析（複素解析）は大学２,３回生で学びます。理屈を抜きにすれば高校数学の微分積分の続きとして読むことも可能です(※2)。

複素平面

複素数$${a+bi \:\:(a, b\in \mathbb{R})}$$と実数の組$${(a, \: b)}$$は１対１に対応するので、複素数$${a+bi}$$を平面上の点として捉えることができます。その平面が複素平面（または 複素数平面）です。

例１　複素数と点との対応

$${3+i \longleftrightarrow (3, \: 1)}$$
$${5 \longleftrightarrow (5, \: 0)}$$
$${-2i \longleftrightarrow (0, -2)}$$
$${0 \longleftrightarrow (0, \: 0)}$$

これを図にすると次の通りです。

左図はアルガン図、右図は例１を図示したもの

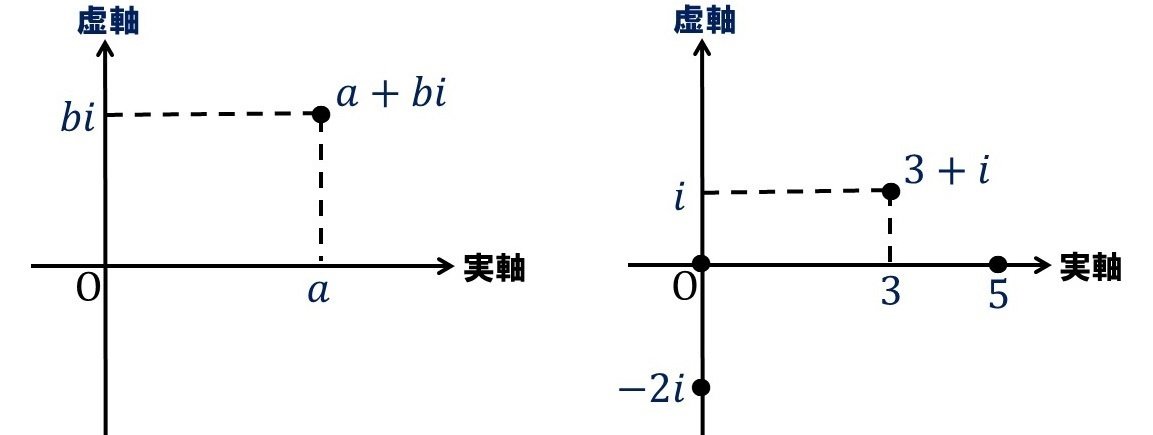
左図がアルガン図と呼ばれるもので、複素平面の横軸を実軸 (ジツジク) 、横軸を虚軸 (キョジク)といい、交点は原点です。

注：複素平面のかき方はいろいろあります。
①矢印を付けたり、付けなかったり
②実軸、虚軸でなく、座標平面と同じくｘ軸、ｙ軸としたり
　（このときは普通に座標平面として書かれます）
③実軸、虚軸の代わりに、それぞれを Re,  Im と書いたり（頭文字２字）
④縦軸、横軸だけで何も書かなかなかったり（専門書でよく見かける）
※ どのかき方を選ぶかは好みですが、高校生の場合は教師の指示に従ってください。

複素数は平面上の点と捉えられるので、複素数$${z}$$を点$${z}$$ということもあります。さらに、複素平面で考えるときには、単に点でなく、ベクトルで捉える方が分かりやすくなります。どういうことかというと

複素数$${a+bi}$$を、単に点$${(a, \: b)}$$ではなく、成分が$${(a, \: b)}$$である原点を基準とする位置ベクトルとみるのです。つまり、複素数$${z}$$をベクトル$${\overrightarrow{\mathrm{Oz}}}$$と考えるのです。

歴史の順序で言えば、座標平面、複素平面、ベクトルなので、複素数をベクトルとみるという考え方はベクトル誕生以後です。

複素数の絶対値

複素数には実数と違って大小関係がありませんが、実数に絶対値があったように複素数にも絶対値というのを考えることができます。実数の絶対値の図形的意味は原点からの距離でした。複素数の絶対値も原点からの距離と定義します。そうすると複素数$${z=a+bi\:\:(a, b\in \mathbb{R})}$$の絶対値$${|z|}$$は次のようになります：

注：$${i=0+1i \longleftrightarrow (0, \: 1)}$$なので$${|i|=1}$$と考えます。

複素数をベクトルと見れば、$${\overrightarrow{\mathrm{Oz}}=(a, \: b)}$$なので、ベクトルの長さ$${\overrightarrow{\mathrm{Oz}}}$$は複素数の絶対値$${|z|}$$に相当し

$${|z|=|\overrightarrow{\mathrm{Oz}}|=\sqrt{a^2+b^2}}$$

となり、同じ結果を得ます。
注：複素数$${z}$$の絶対値$${|z|}$$は実数です：$${|z|\in \mathbb{R}.}$$

例２　$${z=3-4i}$$のとき、$${|z|=\sqrt{3^2+(-4)^2}=\sqrt{25}=5}$$となります。

複素数の和と差の図示

計算の仕方は知っているので、２点$${z, \: w\in \mathbb{C}}$$の和$${z+w}$$および差$${z-w}$$の図示について話します。２つのベクトルの和および差と考えれば説明の必要がないのかもしれませんが、次がその図です：

左図が複素数の和で、ベクトルの和のように平行四辺形を利用します。
右図が複素数の差を図示したものです。２点$${z, \: w}$$を結べばベクトルの差が得られましたが、それは複素数の差ではありません。複素数の場合は原点を基準にした位置ベクトルで考えるので、始点を原点に平行移動させます。なので次のように考えると直接かけます。ベクトルでもやっていることですが$${z-w=z+(-w)}$$と和で考えます。そうすると原点を基準にしたベクトル$${z-w}$$が得られます(※3)。

複素数には積と商もありますが、その話をするには別の準備が必要になるので次回の話です。

複素数の絶対値の性質

複素数の絶対値の性質を紹介すると同時に、実数の絶対値、ベクトルの長さの性質にも触れておきます：

よく使われる性質は①～④です。
複素数の③④⑤の$${\bar{z}}$$は$${z}$$の共役複素数です：$${\overline{a+bi}=a-bi}$$
①～③は実数・複素数・ベクトルともほとんど同じですね。一方、④は対象によって異なるので注意が必要です。

性質①は複素数の絶対値の定義からいえます。性質②③は問題にするので考えてみてください。

問題　$${z=a+bi \:\:(a, b \in \mathbb{R})}$$として、複素数の絶対値の性質②③が成り立つことを確認してください。③については、同一の複素平面上に図示してみてください。気づくことがあると思います。
（答えは少し下にあります）

複素数の絶対値の性質⑤は④から平方根を取ることで得られます。実際、

$${|z|\in \mathbb{R}, \: |z|\geqq 0}$$なので、$${|z|^2=z\bar{z}}$$の平方根をとると$${|z|=\sqrt{z\bar{z}}}$$です。

そこで④が成り立つことを確認します：④ $${|z|^2=z\bar{z}.}$$

$${z=a+bi \:\:(a, b \in \mathbb{R})}$$とすると

$${z\bar{z}=(a+bi)(a-bi)=a^2-b^2i^2=a^2+b^2=|z|^2.}$$

問題の答え
性質② $${|z|=0 \iff z=0}$$について：
$${|z|=0 \iff \sqrt{a^2+b^2}=0 \iff a^2+b^2=0 \iff a=b=0 \iff z=0}$$

補足：$${a^2+b^2=0 \iff a=b=0}$$について
右から左は明らかなので、左から右を説明します。
背理法を使います。
$${a\neq 0}$$と仮定すると$${a^2>0}$$なので$${b^2\geqq 0}$$ですが$${a^2+b^2>0}$$となり矛盾します。したがって$${a=0.}$$ 同様にして$${b=0}$$もいえます。▮

性質③ $${|z|=|-z|=|\bar{z}|}$$について：$${|z|=\sqrt{a^2+b^2}.}$$
$${-z=-a-bi}$$なので、$${|-z|=\sqrt{(-a)^2+(-b)^2}=\sqrt{a^2+b^2}.}$$
$${\bar{z}=a-bi}$$なので、$${|\bar{z}|=\sqrt{a^2+(-b)^2}=\sqrt{a^2+b^2}.}$$

だから、$${|z|=|-z|=|\bar{z}|}$$　が成り立ちます。

図示すると次の通り：

図から、$${z}$$と$${-z}$$は原点対称、$${z}$$と$${\bar{z}}$$は実軸対称と分かります。なので$${|z|=|-z|=|\bar{z}|}$$は明らかです。

問　$${z}$$と虚軸対称の点は何だと思いますか。

答え　求めたい虚軸対称の点は、点$${\bar{z}}$$と原点対称なので  $${-\bar{z}}$$  です。

今回紹介した知識を使えば次のことが分かります：

例３（２点間の距離）

２点$${\alpha=4-3i, \: \beta=2+i}$$間の距離を求めることができます。

$${|\overrightarrow{\mathrm{\alpha\beta}}|=|\beta-\alpha|=|(2+i)-(4-3i)|=|-2+4i|=\sqrt{(-2)^2+4^2}=2\sqrt{5}.}$$

※ ベクトルを使ったのは$${|\beta-\alpha|}$$で求められることの説明をするためです。テストなどで単に問題を解くだけなら、$${|\beta-\alpha|}$$から書き出して構いません。もちろん、$${|\alpha-\beta|}$$でもよいです。
なお、複素数の差の意味を考えると、ベクトルを使わなくても$${|\beta-\alpha|}$$で求められることが分かります。（各自の課題）

例４（不等式の証明）

複素数$${z\in \mathbb{C}}$$に関する不等式を証明することができます。

不等式　$${|z|^2-(z+\bar{z})+1\geqq 0}$$　を示してみます。

　　　　$${|z|^2-(z+\bar{z})+1}$$
　　　$${=z\bar{z}-(z+\bar{z})+1}$$
　　　$${=z(\bar{z}-1)-(\bar{z}-1)}$$
　　　$${=(z-1)(\bar{z}-1)}$$
　　　$${=(z-1)(\overline{z-1})}$$　◀$${\bar{z}-1=\bar{z}-\bar{1}=\overline{z-1}}$$
　　　$${=|z-1|^2\geqq 0.}$$ ▮

注：①最後の等号は複素数の絶対値の性質④を使いました。
②$${a\in \mathbb{R}}$$　ならば　$${a=\bar{a}}$$　ですね。
実際、$${a=a+0i}$$のとき、$${\bar{a}=\overline{a+0i}=a-0i=a}$$だから。

知識として整理すると

　　　　　　　　　　$${z\in \mathbb{R} \iff \bar{z}=z}$$
　　　　　　　　$${z}$$が純虚数 $${\iff z\neq 0 \:\: かつ \:\: \bar{z}=-z}$$

が成り立ちます。後者が成り立つのは

$${z}$$が純虚数 $${\iff z=bi \:\:(b\in \mathbb{R},\neq 0) \iff \bar{z}=-bi=-z, \: z\neq 0}$$

だからです。

今回のポイントは、複素数をベクトルとして捉えることです。まずはこれを修得してください。複素数の絶対値の性質、$${z, \: -z, \: \bar{z}}$$の図形的関係や最後に紹介した内容は後回しで構いません。内容的にもやさしくありません。▢

確認問題

(1)  ２点$${\alpha=2-5i, \: \beta=7+7i}$$間の距離を求めよ．

(2)  不等式$${|z|^2+iz-i\bar{z}+1\geqq 0}$$を証明せよ．ただし，$${z\in \mathbb{C}.}$$

確認問題の答え

(1)  13
(2) 　$${|z|^2+iz-i\bar{z}+1}$$
　$${=z\bar{z}+iz-i\bar{z}+1}$$
　$${=z(\bar{z}+i)-i(\bar{z}+i)}$$
　$${=(z-i)(\bar{z}+i)}$$
　$${=(z-i)(\overline{z-i})}$$
　$${=|z-i|^2\geqq 0.}$$ ▮

※１　歴史の詳細については

ジョン･タバク 著『はじめからの数学３　数』

の pp.145-149 をご覧ください。

※２　複素解析は関数論とも呼ばれます。本を探すときには複素解析だけでなく、関数論も探してみてください。例えば、高校数学の延長でだいたいのことを知りたいのなら

小野寺嘉孝 著『なっとくする複素関数』

が読みやすいと思います。細かい部分は気にせずざっと目を通す感じで１回目を読み、２回目、３回目と少しずつていねいに読んでいくのが良いかと思います。

いやそうでなく、高校数学を含み、少し越したくらいの内容を知りたいのならブルーバックスから出ている

堀場芳数 著『虚数 i の不思議』

がおもしろいと思います。

専門書に分類されると思いますが、一般向けに書かれた複素関数論の本があります。『なっとくする複素関数』は計算重視ですが、こちらは理屈の概要が説明されています。

志賀浩二 著『数学30講シリーズ　複素数30講』

※３　この数学事始めでは、ベクトルの差を２点を結ぶ方法よりも、和を利用した方法を多く使いました。その理由がここにきて分かったと思います。できるだけ統一した見方をしたかったのです。

参考文献

佐藤恒雄・吉田英信 共著『初歩から学べる複素解析』（培風館）
高校数学Ⅲの検定教科書