
31.06 ベクトルの初歩(空間図形の話)
各自の直観に頼って、ベクトルの話を進めることも可能だと思うのですが、その直観はこれまでの生活の中で育まれるものなので、どうしても理解のできないことも出てくると思います。
多くの場合は直観でわかると思いますが、いざというときのために、論理を準備しておきます。高校数学では定義・公理・定理が曖昧に書かれていますが、ここでは明確にします。
なお、この話を読み飛ばしても、特に空間ベクトルで困ることはないと思います。高校数学の教科書 (昔の中学数学の教科書) で十分です。
大切なこと:実際に図を描いて読み進めると理解が深まります。
空間図形の話をすることにした動機
問題 正四角錐O-ABCDにおいて、辺OCの中点をMとするとき、線分ABおよび点Mを含む平面で立体を切断したときの切り口の図形を答えよ。また、その理由も述べよ(※1)。
切り口の図形は等脚台形です。ではその理由を説明できますか。
例えば
線分ABと平面OCDが平行なので、平面で切ったときの辺ODとの交点をNとすると、AB//NMである。AB//DCより、NM//DCとなる。したがってNはODの中点である。さて、△OBM≡△OANよりBM=ANである。以上から四角形ABMNは等脚台形である。▮
と説明できそうです。でもこの説明には欠陥があります。
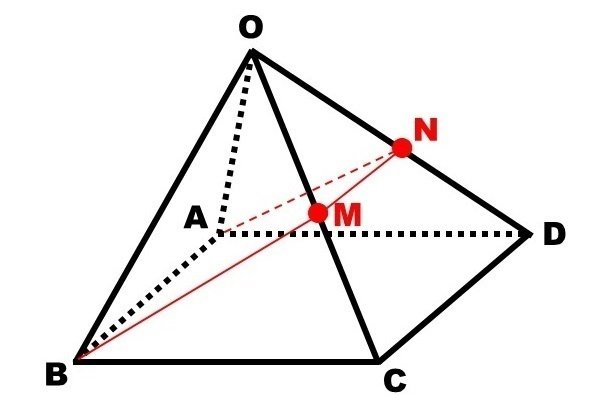
なぜ「線分ABと平面OCDが平行」なのでしょうか。
かんたんに説明できると思っていたのですが、なかなか出来ません。皆さんはできそうですか。
これを解決する過程で知ったのですが、空間内において、3本の直線$${\ell, \: m, \: n}$$において
安心して創作活動が続けられるよう応援してくださると助かります。いただいたチップは書籍もしくは文具の購入に当てたいと思います。

