26.52 図形と方程式（総合問題）

これまで学んだ知識が確認できる問題です。
入試では解けるようにしておきたい必須問題だと思うのですが、数学Ⅱの図形と方程式を終った段階で解くのはやさしくありません。３時間掛かってでも初見で解けるようなら、相当な力があると思います。
力試しをしたいなら、次の問題を問いください。
総合問題として知識を確認したいなら、少し下のヒント付きの問題を解いてください。

問題　座標平面上の点$${P(a, b)}$$が不等式$${x^2+y^2<1}$$をみたす範囲を動くとき、点$${Q(a+b, ab)}$$はどのような範囲を動くかを$${xy}$$平面上に図示せよ。

※ これは岐阜大学で出題された問題を少し変えたものです。
元の問題は不等式が$${x^2+y^2+xy<1}$$でしたが、意味が取りやすいように円にしました。２次式$${x^2+y^2+xy=1}$$は楕円を表し、45度傾いています。原点を中心とし、４点$${(\pm \frac{1}{\:\sqrt{3}\:}, \pm \frac{1}{\:\sqrt{3}\:}), (\pm 1, \mp 1)}$$（複合同順）を頂点とする楕円がそれです。

この問題では知識を確認するのが困難なので、この問題を分解した次の問題を解いてください。

総合問題　元の問題を、小問(1)~(4)を解くことで解決せよ。

元の問題　座標平面上の点$${P(a, b)}$$が不等式$${x^2+y^2<1}$$をみたす範囲を動くとき、点$${Q(a+b, ab)}$$はどのような範囲を動くかを$${xy}$$平面上に図示せよ。

　$${u:=a+b, v:=ab}$$と置く。このとき次の各問に答えよ。
(1) 点$${P(a, b)}$$が不等式$${x^2+y^2<1}$$をみたすので$${a^2+b^2<1}$$である。$${a^2+b^2<1}$$を$${u, \: v}$$で表せ。

(2) $${a, \: b \in \mathbb{R}}$$のとき$${u, \: v \in \mathbb{R}}$$であるが、一般にこの逆は成り立たない。そのような$${u, \: v}$$の組を一つ挙げよ。

(3) $${a, \: b \in \mathbb{R}}$$のとき$${u, \: v \in \mathbb{R}}$$であるための必要十分条件を$${u, \: v}$$で表せ。

(4) 点$${Q(a+b, ab)}$$の動く範囲を$${xy}$$平面上に図示せよ。

総合問題の答え（(4)の答えは問題の答え）
(1) $${u^2-2v<1}$$
(2) 例えば $${u=0, \: v=1}$$
(3) $${u^2-4v \geqq 0}$$
(4) 下図

実線の境界は含み、点線の境界は含まない。交点は含まない。

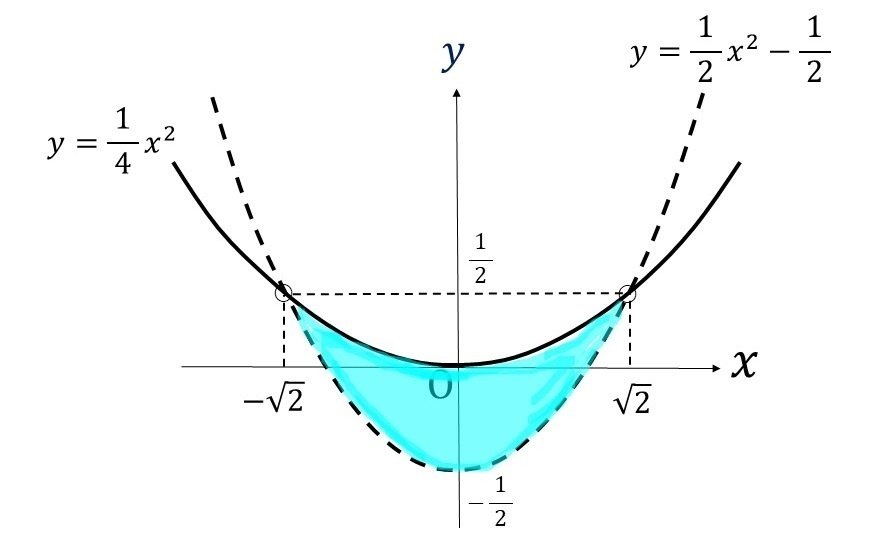
これより下は有料ですが、(1)~(4)があれば独力で解決できると思います。この問題が難しいのは(2), (3)に気づけるかどうかです。方程式でいう検算をする習慣のある人なら初見でも気づけかと思います。