6-1．いまさらきけない平方根（①数の世界）

はじめに
平方根は方程式の話の中で触れようと考えていたのですが、数の世界の話もしたかったので、分けることにしました。次のように話を進めていきます。
①数の世界
②平方根の定義
③ルート記号
④ルート計算（和差，積商，分母の有理化）
⑤ルート計算の理屈
その後に『７．いまさらきけない２次方程式』の話をしようと思います。

では本題に入ります。
これまでは、有理数の世界で話が収まっていました。有理数というのは、整数と分数を合わせた世界のことです。別の言い方をすれば、「比」で表せる数の世界のことです。比というと２：５などを思い浮かべると思いますが、分数 2／5も比と言います。

問題　対角線の長さが２の正方形を書くことはできますね。この正方形の面積を求めるといくつですか。また、この正方形の一辺の長さはいくつですか。

前半はこれまでの知識で解けますが、後半は知らないと解けません。

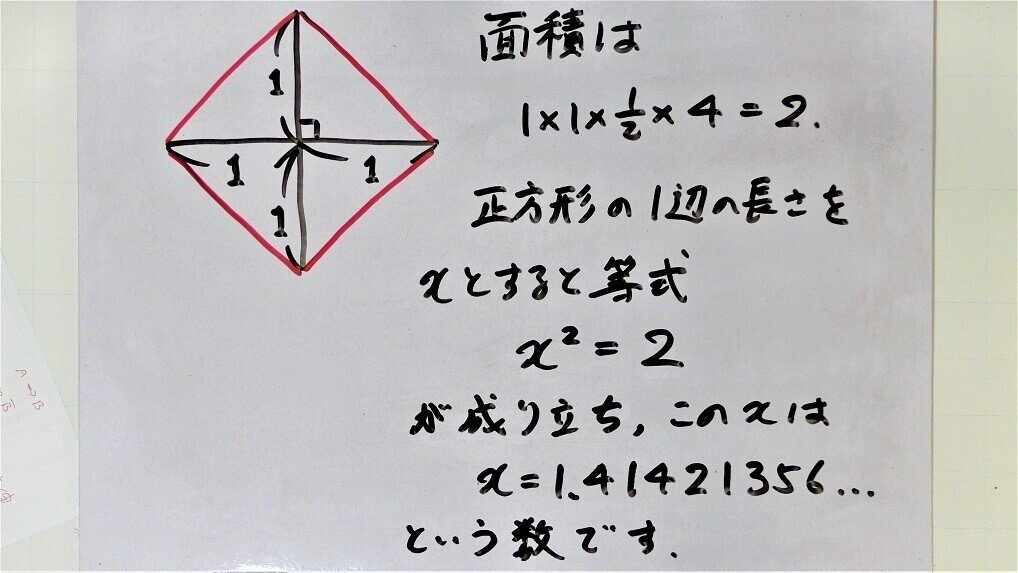
　　　　公式（菱形の面積）＝（対角線）×（対角線）÷２
を使えば、対角線の長さが２の正方形の面積は、２×２÷２＝２ とも求められます。

正方形の１辺の長さをｘとすると、ｘ･ｘ＝２を満たす未知数ｘは有理数ではありません。つまり、比で表すことができない数です。なぜなら、

このような比で表せない数のことを無理数と言います（※１）。有理数と無理数を合わせて、実数(ｼﾞｯｽｳ)と言います。円周率 π (=3.1415926535...)は無理数であり、もちろん、実数です。中高の数学で学ぶ関数はこの実数が前提になっているので、実数という数学用語は覚えておきましょう。

【注】２枚目の図の説明が理解できなくても、気にしないでください。証明に慣れていないなら、なおさらです。論法はホームズやコナンが用いるアリバイの有無で犯人か否かを考えるのと同じです。つまり、容疑者Xが犯人だと仮定したときに、アリバイがあることで矛盾(ﾑｼﾞｭﾝ)が生じるから、Xは犯人でないと考えられる、というものです。

実数の特徴は、「どんな実数も２乗すると０以上になる」ことです。また、加減乗除（＋－×÷）ができ、数に大小関係があります。その大小によって一列に並べると途切れなくすべて繋がって(連続して)います。（※２）

整数も２乗すると０以上になりますが、加減乗はできますが除（割り算）ができません。ただし、余りのある割り算はできます。数に大小関係がありますが、大小によって一列に並べると隙間だらけです。

有理数も２乗すると０以上になるし、加減乗除もでき、数に大小関係もあります。でも、大小によって一列に並べると隙間があるのです。円周率 π や上に述べた２乗すると２になる数などの隙間があるのです。分数があれば隙間なく並んでいると思えるのですが、実際には隙間があるのです。分数で表せない数があることに気づいたピタゴラスたちが、これを秘密にしようとしたのもすなずけますね。（※３）▢

動画をクリックするとみられます。（2021.4/1 6:17以降視聴可）

※１　有理数はrational number、無理数はirrational numberの邦訳です。書名を忘れましたが、「有比数」「無比数」と訳した方が良かったのではないかと書かれていました。私もそう思います。irrationalはrationalの否定です。

※２　実数についてきちんと学ぶこともできます。『実数論』というタイトルの本もあるくらいです。ここに書いたことを慎重に読むと、怪しいことだらけです。それに気づいた人は、次の本を立ち読みでもいいから見てみてください。（次回6-2の表紙）
デーデキント著『数について　連続性と数の本質』（岩波文庫）

※３　いろいろな本に書かれていると思います。私の手元にある本で言えば
今回の表紙にした
ジョン・タバク著『はじめからの数学３　数』（青土社）
の第５章 進展する数の概念（97頁）に書かれています。