
はじめてのシステム思考 #7 因果ループ図 作り方
VUCA(変動性,不確実性,複雑性,曖昧性が高い)時代と言われる現代、複雑な問題に対処する能力がますます求められています。そのような能力の一つであるシステム思考は、戦略,組織,政策,地域,持続可能性など様々な課題領域で、複雑な問題の解決に役立つ思考法です。
このマガジンでは、私が15年ほどシステム思考を学び実践してきたことをもとに、初学者向けにシステム思考の基本を紹介します。(周南公立大学で受け持つシステム思考の講義の一部をnoteにまとめたものです)
この連載を読んでいただきシステム思考を更に学びたいと思った方は、日本におけるシステム思考の第一人者・小田理一郎氏が経営するチェンジエージェント社のHPをのぞいてみるとよいでしょう。システム思考に関連する様々な情報発信やセミナー、研修などが紹介されています。
今回は第7回「因果ループ図の作り方」です。因果ループ図の作成手順と注意点について解説します。
因果ループ図の作成手順
こちらが因果ループ図の作成手順です。

まず、解決したい問題を、問いの形で表現し、問題のストーリー展開を話します。問いの形というのは、「なぜ○○は△△なのか?」とか「どうすれば、○○は△△になるだろうか?」などの疑問形の表現です。そしてこの問題にまつわるストーリー展開、これはパターンに相当するものですが、今回はグラフの代わりに物語として語ります。「最初は何とかだけど、だんだんこうなって、ある時○○が起こって、最後は△△になる」というような形で問題のパターンを共有します。

次に、問題に関わる主な関係者や立場を挙げていきます。これをやることで、後から重要な変数を出しやすくなります。例えば、「なぜ、学力が身につかないのか?」という問題には、学生本人や親、教師、友達などの関係者が関わっていますよね。

そして3番目に、関係者が特に気にしている物事や行動を、変数として表現します。最初からたくさん出すとやりにくいので、まずは大事なものを10個くらいまでにするのが良いでしょう。例えば学力の問題であれば、テストの点数、勉強時間、やる気、教育費、親の干渉度合い、テストの難易度、ノート貸し借り、友達への依存心などです。前回解説した通り、変数は減ったり増えたりする名詞の形で表現し、数値化できないものも重要であれば含めます。

4番目に、最も重要な変数を中心に置き、その変数と他の変数を因果関係の矢印で結んでいきます。例えば、「テストの点数」が最も重要だとして、その要因として「ノート貸し借り」や「勉強時間」が同の矢印、逆に「ノート貸し借り」や「勉強時間」の要因として「テストの点数」が逆の矢印で結べます。
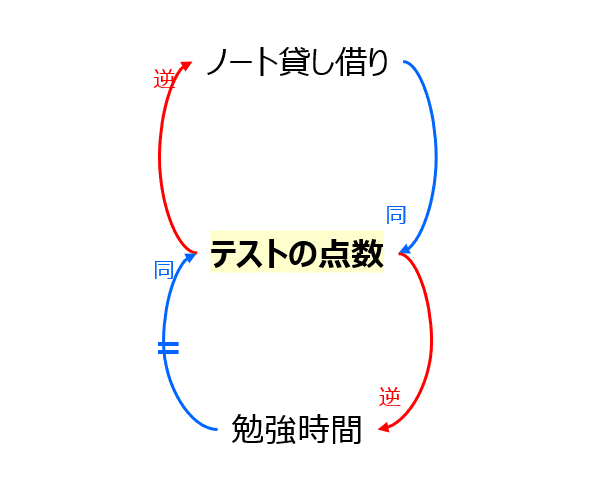
5番目に、他の変数同士も因果関係の矢印で結びながらループを複数作っていき、ループに名前を付けます。ループはその中の逆の矢印の個数によって、自己強化型とバランス型の2種類がありました。例えば、ノート借りてしのぐループ、じっくり実力をつけるループ、学ぶ力が無くなるループなどです。
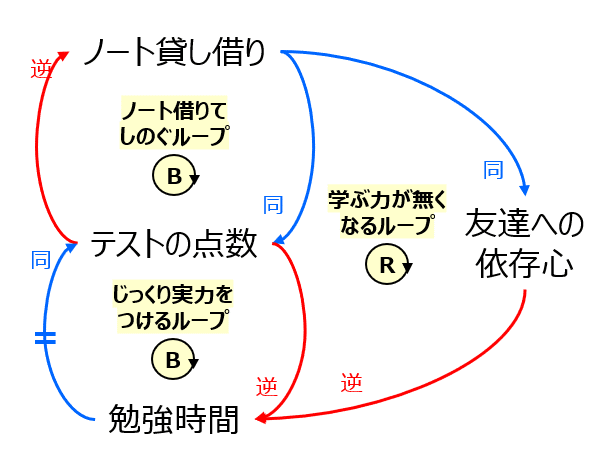
6番目に、ループ図全体をなぞり、こうなったらこうなって、このループが回って、などイメージをしながら、最初に共有したストーリー展開のパターンをこの構造で表せているか確認します。うまく表せていない場合は、手順3、4、5に戻りながら修正していきます。

最後に7番目の「レバレッジポイントを探る」については、第8回で解説します。
以上が作成手順ですが、因果ループ図を書くのは簡単ではありません。ただし正解というものもありません。大事なのは議論の過程でメンバーの考え方の違いを理解しすり合わせていくこと、そして関係者が理解でき、納得できる構造を描くことです。
注意点①変数の抽象度
因果ループ図の作成にあたっての注意点を2つ説明します。1つは変数の抽象度に関する注意点です。
具体的という言葉の対義語が抽象的です。例えば、算数をより具体的にすると演算、図形、グラフなどの要素があります。逆に抽象的にすると教育、さらに抽象化すると学びという概念になっていきます。その言葉がどの程度具体的か?抽象的か?の度合いを「抽象度」と言います。

因果ループ図の変数にする言葉は、具体的で細かすぎず、抽象的でおお括り過ぎない、議論に適切な抽象度にすることが重要です。変数が具体的過ぎると煩雑になり、抽象的過ぎると言いたいことを言い表せなくなります。解決したい問題や議論の目的に対して、ちょうど良い抽象度かどうか?議論する人や説明される人たちの理解が、噛み合う抽象度か?といったことを念頭に置きながら、適切な抽象度に調整していきましょう。
抽象度の調整は最初は難しい事ですが、思考の訓練をしていると次第に身についてきます。
注意点②因果関係
2つ目の注意点は、因果関係についてです。改めて因果関係とは、ある事象が原因となり、他の事象が結果として生じるという関係です。因果ループ図で矢印で結んだものが、本当に因果関係として成り立っているのか?注意が必要です。
今、変数Aを要因、変数Bを結果として矢印を結びました。でもこの因果関係は本当に成り立っているでしょうか?そうではない場合もあります。例えば、変数AとBは直接因果でつながっていないけど、間に別の変数Cがある、という場合。他には、要因は変数Aだけではなく別の要因として変数Cがあり、この2つの要因が重なった結果Bとなる、という場合。他にも、AとBは因果関係ではなく、実は別の変数Cが共通の要因として隠れている場合などです。

全ての矢印をこうやって検証するのは現実的ではないですが、システムの中で特に重要な因果関係や、つながりに違和感がある因果関係は、このような考え方で検証してみると良いでしょう。
第7回「因果ループ図の作り方」は以上です。次回は、因果ループ図で構造を可視化した上で効果的な解決策を探る考え方について解説します。
いいなと思ったら応援しよう!

