構造最適化手法とアルゴリズム

前回の記事で構造最適化問題についてご説明しました。
今回は、最適化問題を解くための手法と、それに用いるアルゴリズムについて解説します。

※この記事はシリーズになっておりますので、初めての方は下の記事をご覧ください。

最適化手法

最適化問題は、変数によって目的変数が変化する関数として捉えることができます。目的関数が最小となる変数を探すために、さまざまな最適化手法が考えられてきました。その手法は「数理計画法」と「発見的手法」の大きく２つに分かれます。
これらの手法から、最適化問題に合わせてアルゴリズムを選択する必要があります。有効でないアルゴリズムを使用すると、時間がかかったり、そもそも解が得られなかったりします。

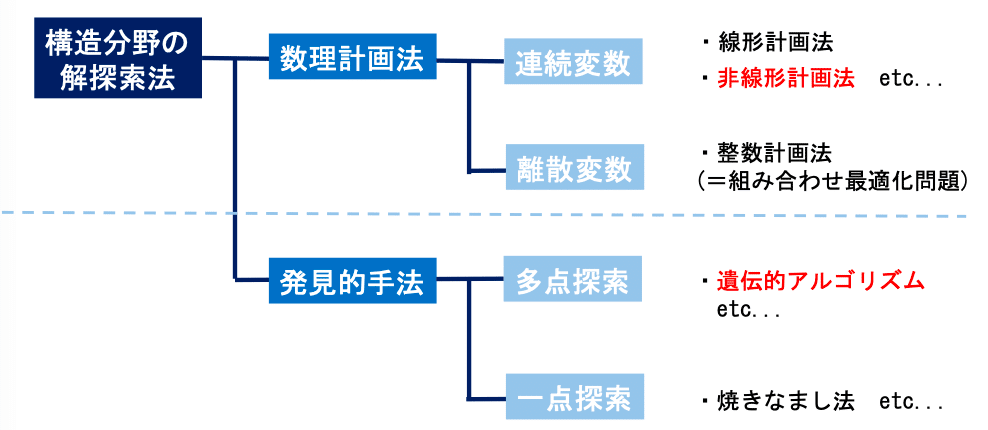
数理計画法

数理計画法は、比較的単純な最適化問題に有効な手法です。
制約条件から数式を予測し、そこから解を求めます。
参考サイト(https://www.msi.co.jp/nuopt/introduction/algorithm/index.html)

このうち、連続変数という分類では、y=f(x)のグラフが連続であるものを言います。
式が線形なものは「線形計画法」
式が非線形なものは「非線形計画法」
を用いることが多いです。

離散変数という分類では、変数自体に「整数」などと離散的な制約がある場合に用います。

数理計画法では、単純な最適化問題に有効であると言いました。
では逆に、複雑な最適化問題とはどのようなものなのでしょうか？

最適化問題には、非凸性という難しい特徴のあるものがあります。

上右の画像のように、凹んだ部分がない関数の場合、素直に最適解を求めることができます。
しかし、左の画像のように凹んだ部分があると、そこに惑わされて正しい解を得ることが難しくなります。

そこで、この問題を解決できるのが発見的手法です。

発見的手法

発見的手法では、まずランダムな変数を解析します。
その後、その解析結果をもとに次の変数を決定し解析する。
またさらにその解析結果をもとに次の変数を決定…というように、繰り返していきます。
この手法では、完全な最適解を見つけることは難しい一方で、複雑な問題でも、最適解に近い答えを見つけることができます。

この時、「次の変数を決定する」ためにさまざまなアルゴリズムが考案されてきました。

代表的なものとして
・山登り法
・焼きなまし法
・遺伝的アルゴリズム
・蛍アルゴリズム
などがあります。

以下のサイトでわかりやすく解説されていますので、ご覧ください。
https://kumagallium.hatenablog.com/entry/2019/07/24/124501

まとめ

ここまで、さまざまなアルゴリズムをご紹介しました。
最適化問題に合わせて手法を選択することは
・時短
・正確性
・そもそも解が見つかるかどうか
と、さまざまなメリットがあります。

数式が出てきて難しい部分もありますが、色々なツールを扱ううちにだんだんと理解できてきますので、ぜひ色々と調べて試してみてください。