NumPyroで大阪の中古マンションデータをベイズモデリング

2022年10月15日 17:42

最近NumPyroなるMCMCを実行するためのライブラリを発見したので、勉強がてら試してみました。

データの読み込みから可視化

Bayesian Regression Using NumPyro という公式マニュアルの超絶わかりやすい解説のJupyter notebookがあります。これを参考にして線形モデルの当てはめまで試してみました。

大阪データの読み込み

前回使った大阪市中央区のデータを一部加工して、必要な列だけに直したものを作りました。まずは必要なライブラリを全部インポートして、データを読み込みます。

import os

from IPython.display import set_matplotlib_formats
import jax.numpy as jnp
from jax import random, vmap
from jax.scipy.special import logsumexp
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns

import numpyro
from numpyro.diagnostics import hpdi
import numpyro.distributions as dist
from numpyro import handlers
from numpyro.infer import MCMC, NUTS

plt.style.use("bmh")
if "NUMPYRO_SPHINXBUILD" in os.environ:
    set_matplotlib_formats("svg")

# assert numpyro.__version__.startswith("0.10.1")

data_file = './data/osaka_data.csv'
df = pd.read_csv(data_file)
df.head(5)
df[['price','room_size','howold_building']].head(5)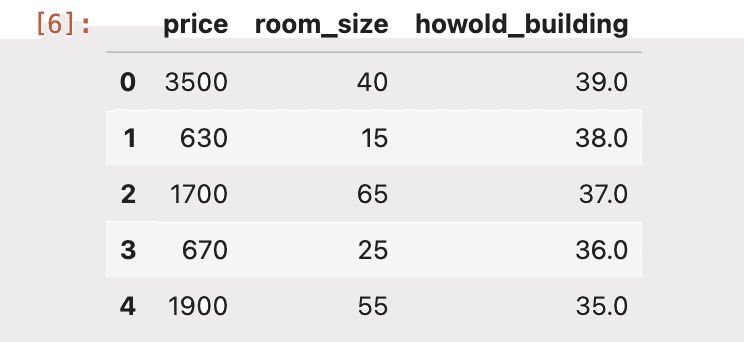

グラフで関係を見てみる。

%matplotlib inline
vars = [
    "price",
    "room_size",
    "age",
    "t_year"
]
sns.pairplot(df, x_vars=vars, y_vars=vars, palette="husl");

価格と部屋サイズの関係を見る。


sns.regplot(x="room_size", y="price", data=df);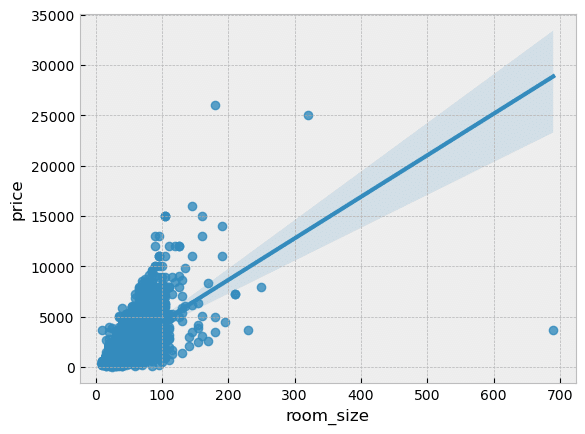

大阪市中央区のデータを全部まとめていますが、前回も見た通り部屋が広ければ価格は高いです。

線形モデルのフィット

まずは簡単なモデルから作っていったほうが理解はしやすいので、価格は面積と築年に比例している、という超単純なモデルを作ります。公式マニュアルのサンプルを読み解いたところがこちら。

def model1(room_size=None, age=None, price = None):
    alpha = numpyro.sample("alpha", dist.Normal(0.0, 10000))
    x1, x2 = 0.0, 0.0
    if room_size is not None:
        beta1 = numpyro.sample("beta1", dist.Normal(0.0, 10000))
        x1 = beta1 * room_size
    if age is not None:
        beta2 = numpyro.sample("beta2", dist.Normal(0.0, 10000))
        x2 = beta2*age
    sigma = numpyro.sample("sigma", dist.HalfCauchy(100))
    mu = alpha + x1 + x2
    numpyro.sample("obs", dist.Normal(mu, sigma), obs=price)

NumPyroのモデルはこうやって関数の中で定義するみたいで、PyMCのように割と理解しやすいです。

最後から二行目を見ると、mu = alpha + x1 + x2となっていて、ここでモデルの式を決めています。日本語にすると、

価格＝切片＋beta1 * 部屋サイズ＋beta2 * 築年

という具合です。x1とx2はそれぞれ上の部分で

x1 = beta1 * room_size
x2 = beta2 * age

と定義しています。ベイズモデリングなので、このbeta1とbeta2が何らかの事前確率分布に従っていますよ、と指定しているのがそれぞれ定義してあって、

beta1 = numpyro.sample("beta1", dist.Normal(0.0, 10000))

と平均ゼロ、分散10000の正規分布に従っていますよ、と宣言しています。Stanだとここは標準偏差だったりするので、分散なのか標準偏差なのかよくわかりませんが、いずれにせよ結構大きな値、小さな値を取る可能性がありますよ、としています。beta2も同じです。

最後に価格は「切片＋beta1 * 部屋サイズ＋beta2 * 築年」で計算した値を平均値として、正規分布に従っています、と宣言しています。

numpyro.sample("obs", dist.Normal(mu, sigma), obs=price)

ここでsigmaというのが出てきますが、これが正規分布の標準偏差で、二行上で、

sigma = numpyro.sample("sigma", dist.HalfCauchy(100))

sigmaはHalf Cauchy分布に従っていますよ、としています。Cauchy分布のパラメータをなんと呼ぶのか分からないのですが、英語ではlocation parameter（普通はゼロ）とscale parameterと呼んでいます。sigmaは正規分布の標準偏差として使いたいので、０より大きい値を取るように事前分布でHalf Cauchyを使っています。

MCMC実行

# Start from this source of randomness. We will split keys for subsequent operations.
rng_key = random.PRNGKey(0)
rng_key, rng_key_ = random.split(rng_key)

# Run NUTS.
kernel = NUTS(model1)
num_samples = 2000
mcmc = MCMC(kernel, num_warmup=1000, num_samples=num_samples)
mcmc.run(
    rng_key_, room_size=df.room_size.values, age=df.age.values, price=df.price.values
)
mcmc.print_summary()
samples_1 = mcmc.get_samples()

rng_keyというのがよく理解できていないですが、乱数を発生させるためのシード値のようなものを与える必要があるようです。NUTSという関数に先ほど定義したモデル式の関数を与えます。で、結果がこちら。

beta1が面積に対する係数、beta2が築年に関する係数です。それぞれ44と-56で、前回記事の最終モデルの中で推定された係数がそれぞれ43と-58だったので、ほぼほぼ同じ結果が出ていることが確認できました。

NumPyroの感想

これまでBUGSから始まって、JAGS、Stan、PyMCと色々と使ってきましたが、メインで使ってきたのはRでのStanでした。Stanは本もたくさん出ていて使いやすいのですが、ネックはモデルのコードを別のファイルに保存しないといけないことで、これが面倒でした。NumPyroはPythonで動くのと、モデルのコードもPyMCのように同じファイル内に記述することができるので、これは便利でした。

一方でまだまだ使っている人が少ないのか参考資料が少ないのがデメリットでしょうか。以前やったような東京と大阪での階層モデルはどうやったら良いのかがまだ分からず、苦戦しています。ただし公式マニュアルにさまざまな問題への応用事例を解説した資料がそろっているので、英語が読める人はそれほど苦労せず学べるのではないでしょうか。

まとめ

NumPyroの試用記事でした。WinBUGSを使ってマウスで操作をしていた頃を思えば、Pythonのコードだけで実装できて便利な世の中になったな、と思いました。