
Numbers for iPhone - ㉝ 分散図(scatter plot)
Numbersには、分散分析(ANalysis Of VAriance, ANOVA) 用の初歩的指数が用意されている。そのための分散図が用意されている。
文中で用いるファイル(タップすればダウンロードできる)
日付という項目と、最高血圧と最低血圧というデータ列を選択して、最上部の「+」アイコンをタップ
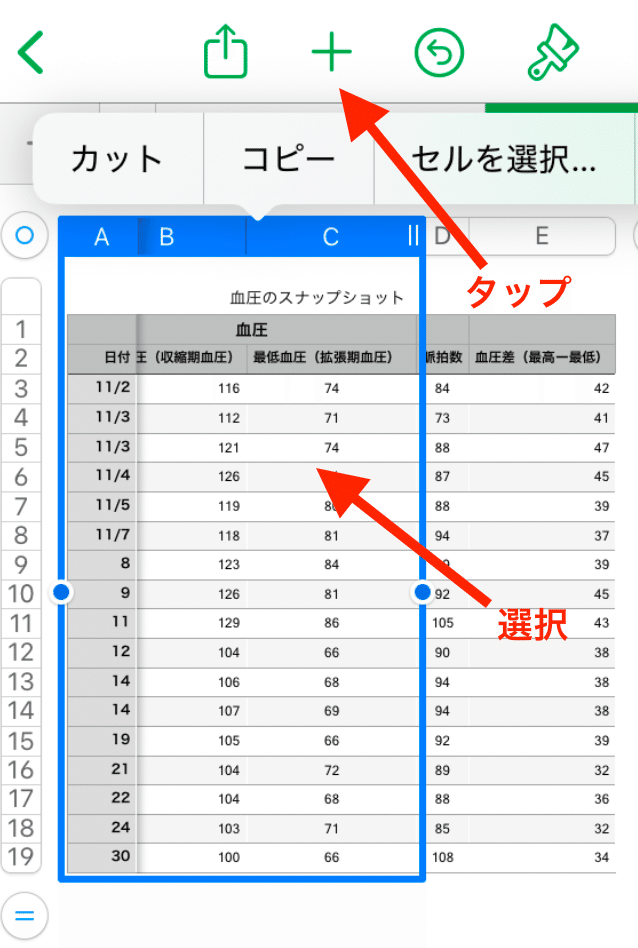
2.表示されるダイアログの最上部からグラフのアイコンをタップし、折れ線グラフのアイコンをタップ

3.折れ線グラフを見やすくするために、最上部のフォーマット・アイコン(刷毛の形)をタップ

4.下に表示されるダイアログの最上部に表示される「データ」というタブをタップして、「Y軸目盛り」をタップ

5.グラフを見ながら、上下に余裕を持たせるように最大値と最小値を決め、目盛りが整数になるように「目盛り数」を調節
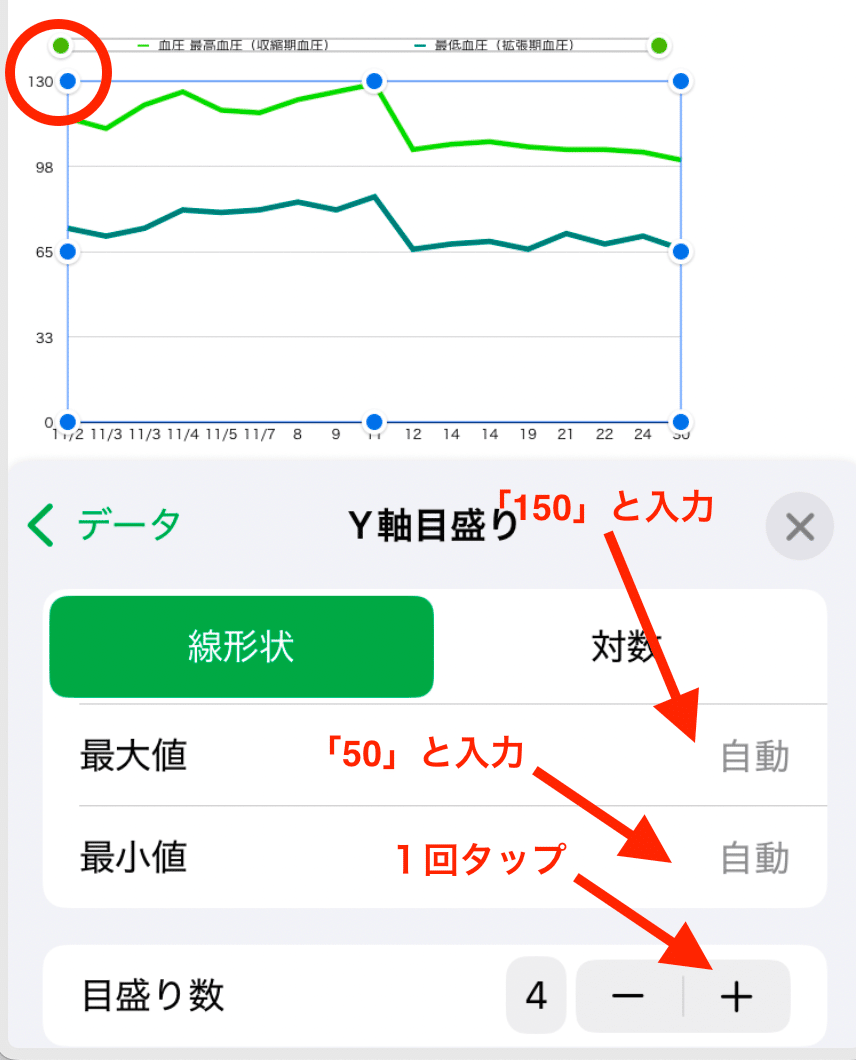
6.うまくできれば、右上の⊗をタップして、終了

さて、作成できたグラフをよく見てみると、動きが連動しているように見える。

両者に関係があるのかどうかを確認するため、分散図を作成する
表の項目を選択後、「+」印をタップして、グラフ・タブをタップし、一番下の右側の分散図アイコンをタップ

2.分散図が作成されるが、X軸とY軸の値が不適切なため、綺麗に表示できない

3.そこで、最上部のフォーマット・アイコン(刷毛の形)をタップ

4.下から現れるダイアログの最上部に表示される「データ」タブをタップし、「X軸目盛り」をタップ
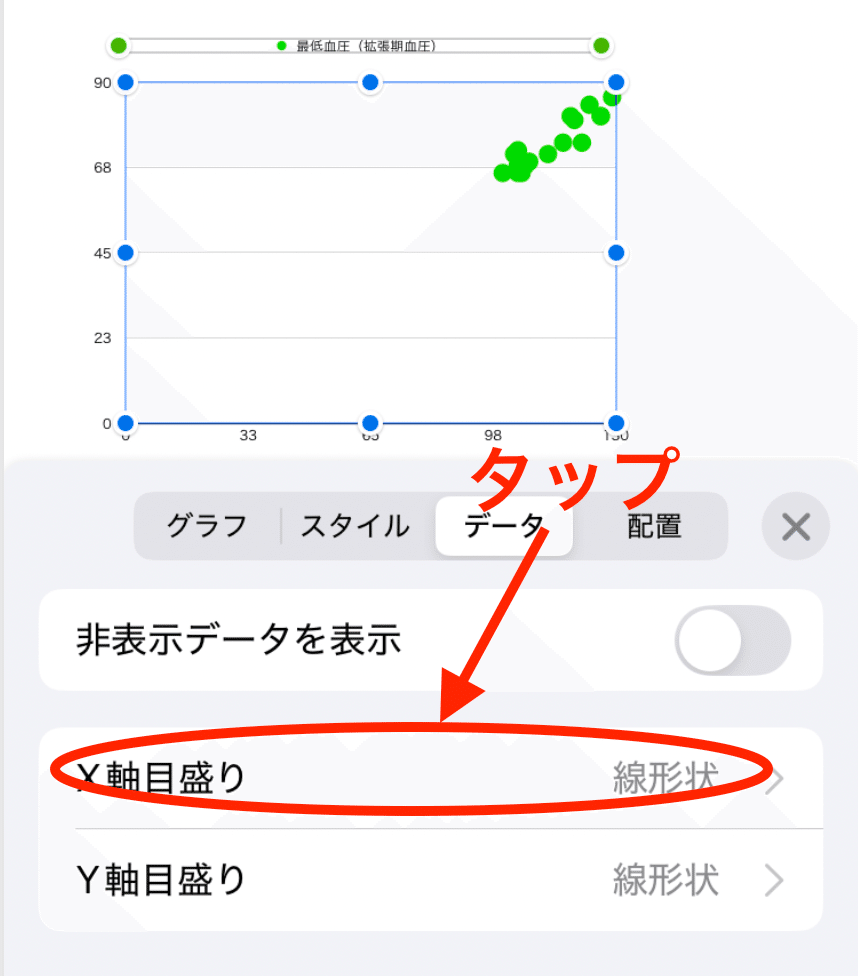
5.X軸目盛りは、最大血圧なので、上下に多少の余裕を持たせるように、最大値と最小値を決め、「目盛り数」を整数になるように調節

6.Y軸目盛り(最低血圧)も同じように調節し、「グラフ」タブをタップして、「トレンドライン」をタップ

7.「R2乗値」をタップ
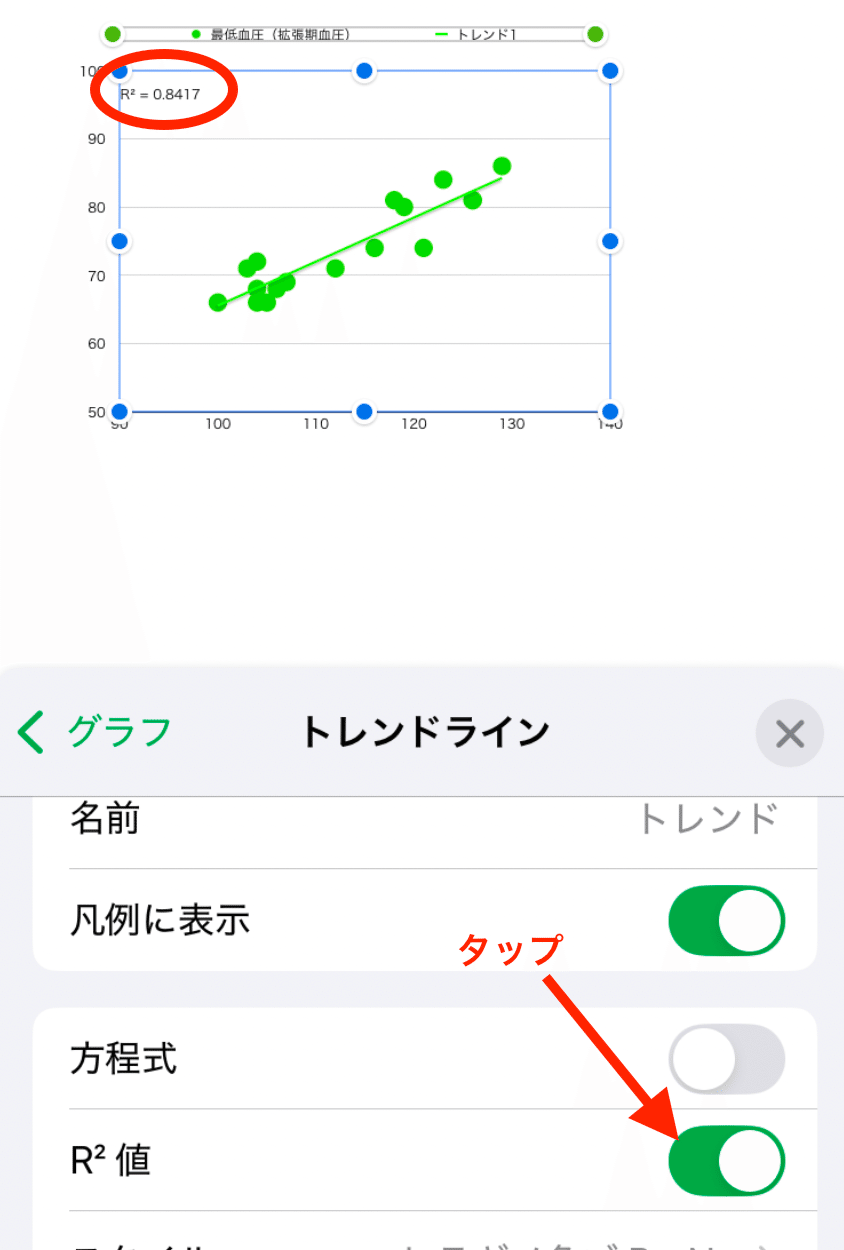
8.R2乗値が0.84であることが分かる。Fratioは、0.84 ➗(1-0.84)✖️20(観察値の数)なので、100以上になり、棄却率が0.0000以下になることが分かる。

つまり、この二つの数値が連動する偶然性は、ほぼない(帰無仮説が棄却される)ので、両者は、正比例の関係にあることが分かる(ANOVA)。
最後の部分は、より精密な統計解析ソフトを用いて立証するが、Numbersでも、大体のことが分かるようになっている。
