
【ゲーム理論】確率論的に最大レートを達成に重要なことを解説します
こんにちは!お久しぶりです。
今回は、教育系とは打ってかわって、ゲーム理論について考えていきたいと思います。
対戦ゲームには、レートというシステムを導入して、ランキングを競うものがありますよね。
今回は、対戦ゲームの中でも、複数人の対戦ゲームについて、確率論的な観点から、最大レートを達成する戦略を考察したいと思います。
この記事でお伝えしたい結論は以下の通りになります。
「最大レートを達成する上で平均順位は当然大事だが、時には平均順位を犠牲にしてでも順位の分散を大きくする必要がある」
です。
これだけ言われてもいまいちイメージがつかないと思うので、どういうことなのか、順を追って解説します。
まず最初に理解しないといけないことは、分散とは何かです。
分散とは、平均順位からのズレの大きさのことです。
例えば、平均順位が5位だったら、4位や6位の割合が多いよりも、1位や10位の割合が多い方が、分散は大きくなります。
ここから先は分散についてわかっていないと理解するのが難しいので、
そのような場合は先に文献[1]などを読むことをお勧めします。
それでは、本編に入っていきましょう!
1. 1位狙い vs 一つでも上の順位狙い
複数人対戦ゲームが、2人対戦ゲームと大きく違うのは、順位について、大きく分けて2つの戦略が取れることです。
それが、見出しにも書いた
1位を狙う戦略
か
一つでも上の順位を狙う戦略
か
です。
2人対戦のときは単純です。
ただ、相手に勝つことだけを考えればいい。
でも複数人で対戦するときは、順位がつきます。
このとき、
リスクを冒してでも1位を積極的に狙っていくか、
無難に一つでも上の順位を狙っていくか
でプレイスタイルが変わってくる場合があります。
例えば、人気ゲームマリオカート。
12人対戦で、順位に応じてレートが増減します。
当然、上位ほどレートがたくさんもらえて、下位ほどレートが大きく減ってしまいます。
確か、6位前後でレートのプラスマイナスが変わってきた気がします。
だから、1,2位をガンガン狙っていくか、まずは6位以上を目指して、そこから一つでも上の順位を目指すかという二つの方針がとれます。
この2つの戦略は、具体的にはどのような面で変わってくるのでしょうか。
わかりやすい例として、ショートカットが考えられるでしょう。
ショートカットは、成功すると一気に上位を狙うことができます。
ただし、失敗すると一気に下位に下がってしまうリスクもあります。
自分が現在4位だとしましょう。
このまま、安定したプレイを続けていればレートがプラスになることが期待できます。ただし、一位とは距離がそこそこあるようです。
さて、ショートカットが狙えるスポットがきました。
あなたは、ここでショートカットにトライするか、それともやめておくか。
もちろん今の自分のプレイスキルによるとは思いますが、1,2位を狙っていくなら、トライするべきでしょう。
反対に、安定して6位以上を狙っていきたいなら避けるべきでしょう。
このように、順位の狙い方によって、プレイヤーの取るべき選択肢が変わってくるのです。
(ショートカットなんてみんなできるんだからできないと話にならないとかそういうツッコミはなしで。あくまで例えです。)
では、どちらの戦略の方が、最大レートを到達するのに有利なのでしょうか。
答えは、「それだけではどちらとも言えない」
です。
もし、どっちの方がいいってはっきり言えたら、それを結論に持ってきてます(笑)
ただし、自分の取りうる成績から、どのように立ち回ればいいか、その方針を決めることができます。
次のことを念頭において、この後の説明を読み進めてください。
リスクを冒してでも1位を狙う戦略は、下位を取る可能性も多くなるので順位の分散が大きくなる
安定をとって一つでも上の順位を狙う戦略は、成績が安定するので順位の分散が小さくなる。
厳密には違うけど、大体そのようなイメージはできるかと思います。
2. 最大レート達成確率を決める要素 平均順位と分散
最大レート達成確率を決める要素には何があるでしょうか。
ここでは、プレイヤースキルではなく、確率論的観点から、つまり、確率分布から考えていきます。
プレイヤーのレートの分布を考えてみます。
確率分布を構成する要素はなんでしょうか。
そう、確率密度関数、さらには平均と分散といったパラメータですね。
レート分布の確率密度関数を考えるのは困難なので、今回は、平均と分散について考えていきます。
レート分布の平均・分散は、順位の平均・分散に対応づけられます。
実は、確率論的に、レートの達成確率を決めるのは平均順位だけではありません。
分散も関わってきます。
もっというと、分散は、大きいほど有利です。
ここで、冒頭でさらっと書いた私の結論を振り返ってみましょう。
私がこの記事で伝えたい結論は、
「最大レートを達成する上で平均順位は当然大事だが、時には平均順位を犠牲にしてでも順位の分散を大きくする必要がある」
でした。
つまり、分散が大きいことはアドバンテージで、そのアドバンテージが平均順位のアドバンテージを上回る場合があるのです!
この理由を次の節で解説したいと思います。
3.確率分布を考えれば明らか
その理由は、理由は確率分布を考えれば明らかです。
例えば、以下の図1を見てください
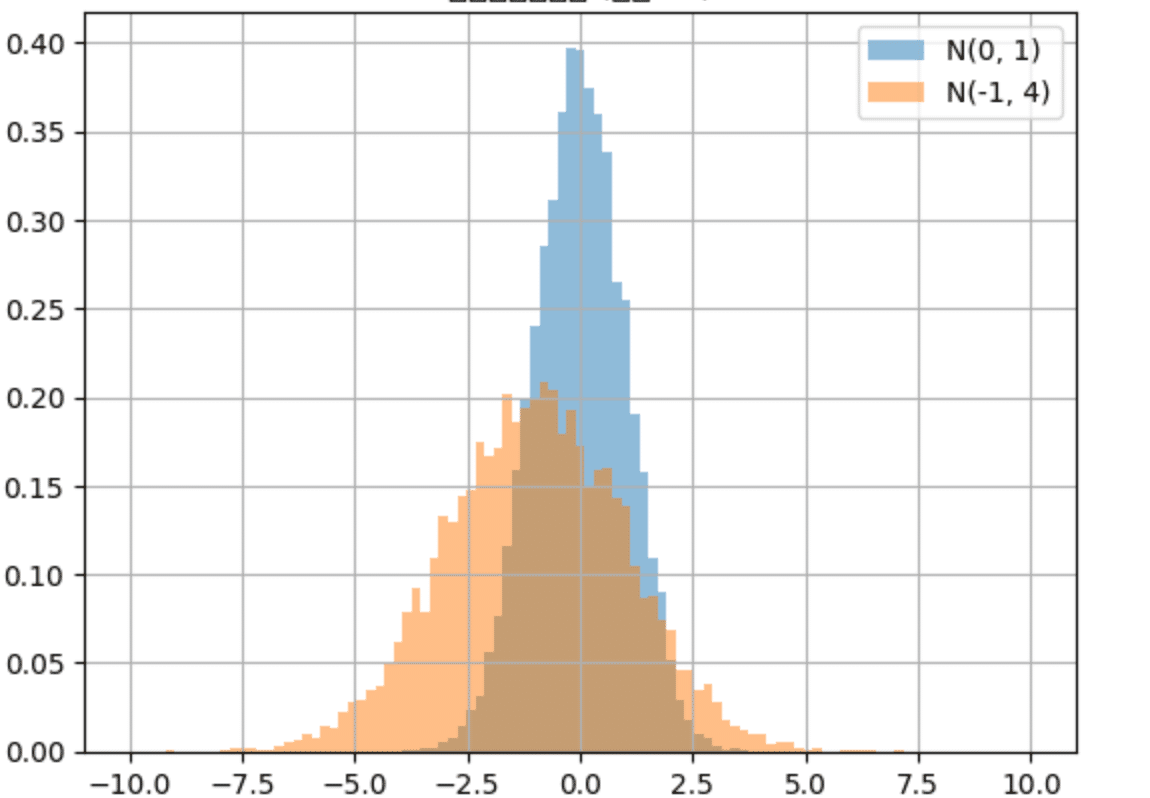
これは、二つの正規分布N(0,1)とN(-1,4)を並べたものです。
どちらも面積は1にそろえています。
正規分布がよくわからないって人は、今は世の中の代表的な確率分布とだけ思ってくれればOKです。
詳しく知りたいって方は、文献[2]などを参照してみるといいかもしれません。
それで、一つ目の正規分布N(0,1)は、平均が0,分散が1であることを示しています。(青色)
二つ目の正規分布N(0,4)は平均が-1,分散が4であることを示しています。(オレンジ色)
例えば、異なる2人のプレイヤーのレート分布が、それぞれこのN(0,1)とN(0,4)になったとします。
このとき、それぞれのプレイヤーがあるレートGより上に位置する確率は、それぞれの確率分布のx>Gの部分の面積になります。
(確率分布って確率の分布だから、面積の総和が確率の総和だよね)
これをみると、分散の大きいN(-1,4)のプレイヤーの方が、高レートに位置する確率が大きいことがわかります。
もちろん、低レートに位置する確率も大きくなるので、一定のレートを維持することが目標ならN(0,1)の方がいいのでしょうが、今回の目標は最大レート到達です。
分散が大きいことが目標達成の上でアドバンテージになることが理解できたのではないでしょうか。
同じように、結論も正しいとわかります。
平均順位は、レート分布上の平均が小さいN(-1,4)の方が悪いですが、高レートに到達する確率はN(-1,4)の方が高くなっています。
このことから、
「最大レートを達成する上で平均順位は当然大事だが、時には平均順位を犠牲にしてでも順位の分散を大きくする必要がある」
ということがいえるのです。
4.まとめ
ここまで読んでくださり、ありがとうございます。
確率論的な観点から、最大レート達成において、平均順位と分散の大きさが大事なことがわかっていただけたと思います。
また、1節にて1位狙いの戦略と、一つでも上の順位を目指す戦略、どちらがいいのかを考えていました。
その答えも保留していましたが、ここで詳細な結論を出しましょう。
平均順位が下がるリスクよりも分散のアドバンテージが大きくなるなら1位狙いをしていけば良いし、下回るなら一つでも上の順位を目指した方が良い
ということになります。
改めて、最後まで読んでくださり、ありがとうございました!
5. 参考文献
今回は、分散、正規分布など、人によっては馴染みがない概念が出てきました。
それらについて、この記事では詳しく解説する余裕がなかったので、参考になるサイトを紹介します。
[1]「分散とは?公式や求め方、計算問題をわかりやすく解説!」受験辞典
[2]「正規分布とは?初学者向けにわかりやすく解説」DATA VIZ LAB
この記事が気に入ったらサポートをしてみませんか?
