高校数学で理解する感染症の拡大と防止策：SIRモデルと等比数列

2020年の初め頃から，新型コロナウィルスが拡大し，私たちの生活も一変しました．特に，緊急事態宣言が発令された2020年4月ごろには，人との接触を控えるような生活スタイルが励行されました．この生活スタイルには"接触を減らすことで感染拡大を防ぐ"という目的がありました．では接触を減らすと，どの程度感染拡大が軽減されるのでしょうか．このnoteでは，高校数学で学ぶ「数列」を使って，この感染症の拡大と防止策としての接触回避の効果を確認します．

なお，先んじてこのnoteの参考文献を挙げておきます．
・稲葉寿編著，2008，『感染症の数理モデル』培風館．
・新居俊作，2020，『コロナの感染拡大と終息の予測方法』https://www2.math.kyushu-u.ac.jp/~snii/SIR.pdf（2021年1月1日アクセス）．

感染症の広がりをとらえる：SIRモデル

このnoteでは，SIRモデルという感染症拡大を表現するモデルを用います．SIRとは，Susceptible（感受性：感染する可能性のある人），Infectious（感染性：感染している人），Recovered（回復：治った人）の頭文字です．SIRモデルは，まだ感染に至っていない人が，感染した人との接触によって感染し，その後回復する，というプロセスを想定しています．

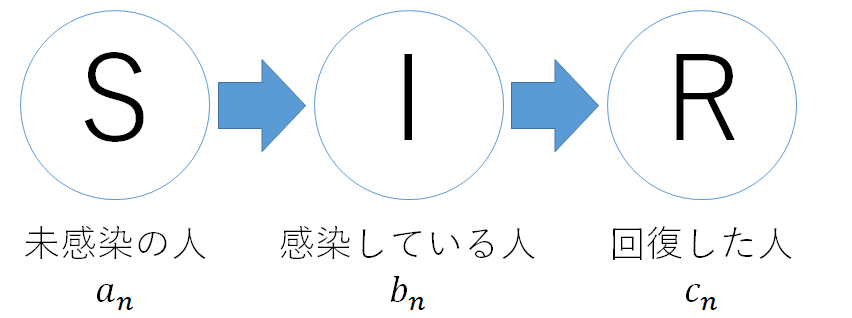
数列の記号を使って，それぞれの段階にいる人の割合を表しましょう． 感染のプロセスのそれぞれの段階をa,b,cの記号を使って表します（以下，note表記の制約上，数列を本文ではa(n), b(n), c(n)とあらわします）．

添え字のnは何日目かを表しています．このa, b, cは時々刻々と変化していきます．典型的なSIRモデルのふるまいをまずは見てみましょう（なお，本noteのグラフはmathematicaを使って描画しています）．

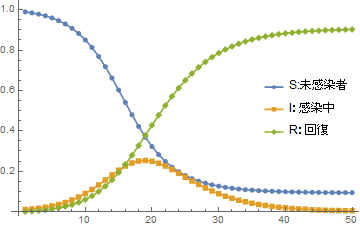
図１ 典型的なSIRモデルのふるまい（β=0.5, γ=0.2, b(1)=0.01(人口の1%)，横軸：n（日数））

未感染者が減少し，感染者が増加するものの，ピークを過ぎると減少し，回復していく流れがわかると思います．この変化を生み出しているのは，高校数学で学ぶ漸化式と，そこに組み込まれた接触による感染というプロセスです．

接触による感染：SIRモデルの漸化式

漸化式とは，数列における変化をとらえるための道具になります．今回のSIRモデルの文脈で言えば，それぞれの段階の1日分の増減をモデル化したものになります．たとえば，左辺のa(n+1)-a(n)は，n+1日目の未感染者割合a(n+1)から，n日目の未感染者割合a(n)を引いたものなので，1日分の未感染者割合の変化を表すことになります．一方，右辺には未感染者割合の増減がどのようにしてもたらされるか，そのメカニズムを反映した式が入ります．

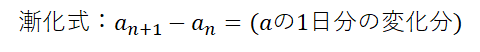
SIRモデルは3つの連立方程式になります．このモデルは外部との人口移動がない場合を想定しています．

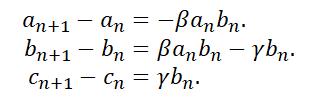
このモデルの漸化式には，接触による感染が組み込まれています．まずは未感染者の変化を表すaの漸化式を見てみましょう．

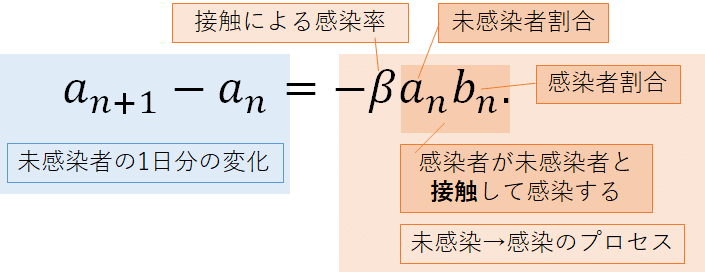
左辺は未感染者の1日分の変化を示しています．右辺は感染者が未感染者と接触することによって，未感染者が感染者になっていく流れを表しています．

感染者が生活のなかで接触をすることを考えます．未感染者と感染者との接触の数は未感染者割合a(n)と感染者割合b(n)に比例します．具体的に言うと，未感染者が6人，感染者が3人のとき，生じうる接触は6×3=18になります（図2にイメージを示しました）．割合でも同じようなことが言えるでしょう．

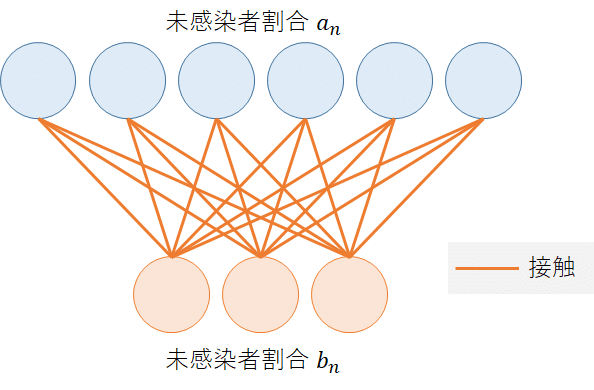
図2 未感染者と感染者との接触の数は互いの割合の積に比例する

β（読み方は「べーた」）は起こりうる接触のうち，どのぐらいの割合で感染が生じたか，をあらわすことになります．それらの積βa(n)b(n)は，感染してしまった未感染者の割合を表すことになります．よって，未感染者割合a(n)の漸化式は，この積にマイナスを乗じる（未感染者が減少する）ように表されます．

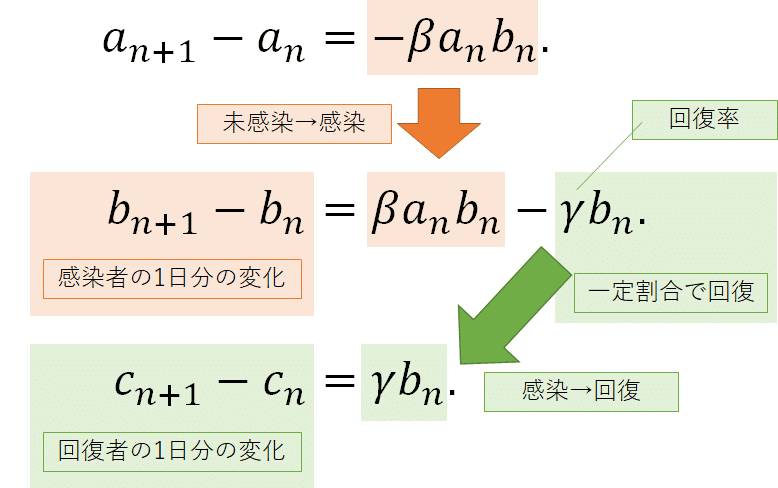
b(n)とc(n)の漸化式も説明しましょう．b(n)の漸化式（感染者割合の変化）には2つの要素が絡んできます．a(n)の漸化式でも登場した新規に感染した人の割合がプラスされる一方（+βa(n)b(n)），感染者の中から一定の割合で回復していく（減らされる）項が追加されています（-γb(n)）．ここで回復率をγ（読み方は「がんま」）と表記しています．c(n)の漸化式は回復者の増減を表します．回復者は感染したのちに回復した人が毎日追加される（+γb(n)）ことになります．

この漸化式は，高校数学で学ぶような方法で解く（a(n)=(nだけの式)にする，一般項を求める）ことはできません．しかし，愚直に数値を代入していくことで，a(n)，b(n)，c(n)の変化を追うことができます．それが図1に表れています．

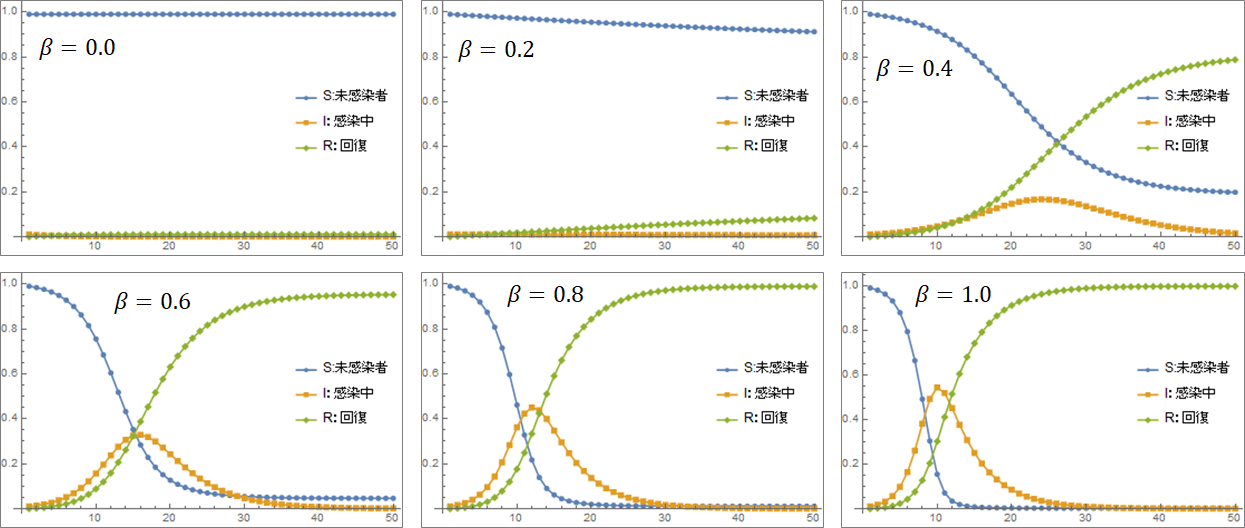
図3 SIRモデルのふるまい（回復率γ=0.2で固定）

別の数値でもSIRモデルの図を見てみましょう．図3に感染率βを変えたものを示しました．回復率γは0.2に固定されています．感染率βが回復率γ=0.2より小さいか等しいとき（β=0.0, 0.2）には，感染者割合b(n)（グラフではオレンジ色）は増加しません．しかし，回復率βが回復率γ=0.2より大きい場合（β=0.4以上）には，増加していることがわかります．

この増加の条件を，等比数列との対比から見てみましょう．

感染が増大する条件：等比数列との比較

等比数列というものは，次の数列のように一定の数がかけられていく数列です．この時，かけられる数は公比というものです．

等比数列の例：1, 2, 4, 8, 16, 32, ……

等比数列は，a(n+1)とa(n)の関係式（漸化式）として次のように書かれます．なお，rは公比です．

等比数列のふるまいは公比rが1より大きいか否かによって決まります．公比が1より大きいときはa(n)は増え続け，1より小さいときはa(n)は0に近づいていきます．図4に実際の数値例を示しました．

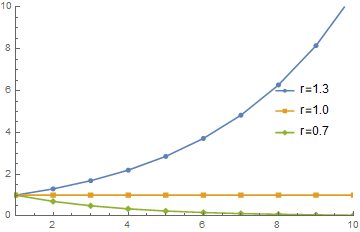
図4 等比数列と公比の関係（a(n+1)=ra(n), a(1)=1のとき）

さて，この知識を踏まえてSIRモデルの感染者率b(n)の漸化式を見返してみましょう．いま，関心があるのはこのb(n)が増加していくのか，減少していくのか，ということです．増減を等比数列の公比から考えてみましょう．

b(n)の漸化式を等比数列のように書き換えます．

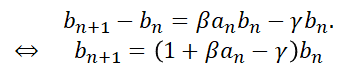
このとき，公比に相当する部分は(1+βa(n)-γ)の部分になることがわかります．a(n)が入っているので，時々刻々と公比が変化するような，少し特殊な等比数列とみなすことができるでしょう．

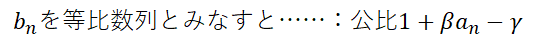
そうすると，感染者割合b(n)が増加する条件は公比が1未満であること，つまり1+βa(n)-γ<1が条件となります．

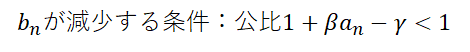
この条件を未感染割合a(n)について整理すると次のように式変形できます．

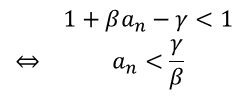
つまり，未感染者割合がある一定数γ/β以下まで減少すると，増加がとまるということです．さきほどのグラフのβ=1.0のグラフを例にふるまいを見てみましょう．

図5 感染者割合の増加とγ/βの関係

γ=0.2，β=1.0のとき，γ/βは0.2/1=0.2となります．なので，未感染者割合a(n)（グラフ中だと青い線）が0.2を割り込むまで感染者割合b(n)（グラフ中だとオレンジの線）は増加し続け，逆にa(n)が0.2を割り込むとb(n)は減少に転じます．グラフ中では，10日目にb(n)の増減が逆転していることがわかります．（ちなみに，このγ/βの逆数β/γは基本再生産数と呼ばれています．）

感染拡大を止めるには：モデルからわかること

γ/βが増減のカギを握っていることがわかりました．そうすると，感染者割合をできる限り減らすために考えるべきことは，このγ/βを大きくすることでしょう．γ/βが大きければ，未感染者割合a(n)が大きい場合であっても，感染者割合b(n)は減少に転じることができます．

では，実際にγ/βを大きくするにはどうすればよいでしょうか．数学的には2つの方策があります．
　1) 回復率γを大きくする
　2) 接触による感染率βを小さくする

「1) 回復率γを大きくする」ためには，現実には治療法の確立や対症療法を効率化するなどが挙げられます．しかし，回復率γを大きくするのは技術革新や体制の強化が必要ですので，すぐにはできません．時間がかかるのです．

一方，「2) 接触による感染率βを小さくする」は接触を減らすことでβを小さくすることができます．あるいは，手洗いやうがい，マスクをつけることでも小さくできるかもしれません．こちらは実行に移しやすいでしょう．緊急事態宣言時に提言されていた「8割の接触を減らす」という目標は，この考えに基づいているといえるでしょう．

実際に，接触をピーク前に8割減らした場合のSIRモデルを見てみましょう．図6にβ=1.0, γ=0.2の場合にピーク前の8日目から接触を8割減らした（β=0.2にした）ときのグラフを示しました．

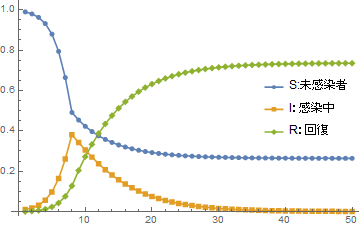
図6 接触を8割減らしたときのSIRモデル（β=1.0から0.2へ, γ=0.2, b(1)=0.01）

接触を減らした8日目から，感染者割合が急激に減少していることがわかります．これは，βが1.0から0.2に減少したことで，γ/βが0.2/0.2=1.0となり，感染者割合b(n)が増加する条件であったa(n)<γ/βを満たすようになったからです．

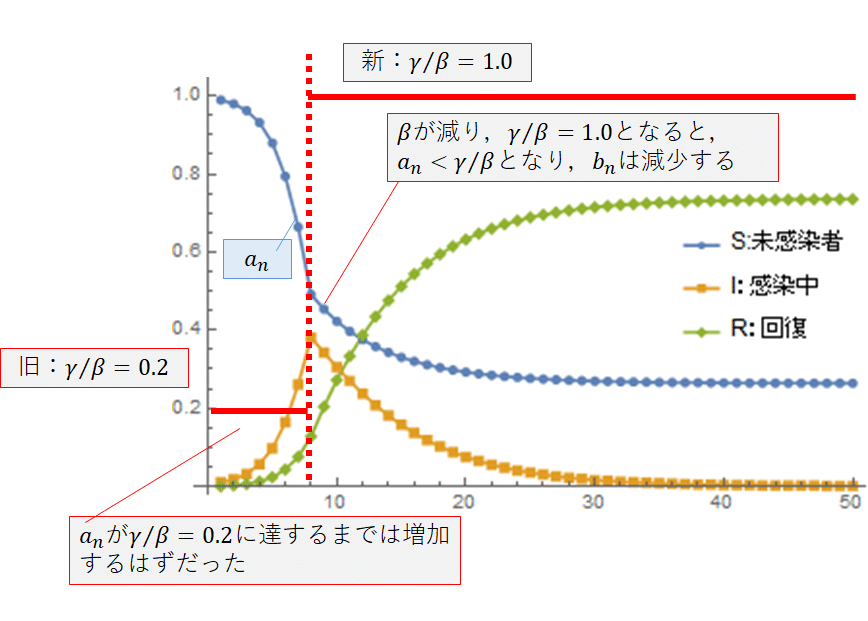
図7 βが途中で減少した場合の感染者割合の増加とγ/βの関係

SIRモデルからわかった拡大防止策の効果

このnoteではSIRモデルという「接触による感染」という概念を軸にしたモデルを見ながら，接触を減らすことの意味を見てきました．実際，接触を減らすことは感染者割合を減少させる，という意味では非常に大きな意味を持ちます．

今後，ワクチンの登場など新型コロナをめぐる攻防は新たな局面を迎えています．しかし，まだまだ「接触を減らす」という拡大防止策は効果を持ち続けるでしょう．

-------------------------------------------

補足1：モデルのありがたみ

このような数理モデルにはしばしば「現実を反映していない」という言葉が投げかけられます．数理社会学が専門の私もよく言われます．しかし，分析者の立場からすれば，数理モデルで現実すべてを表せるという考えは毛頭ありません．最初からそれは無理だとわかっているからです．

では，なぜ数理モデルを使うのでしょうか．それは次の2つの理由があると私は考えています．
　1) 重要なメカニズムを抽出して，「もし○○だったらどうなるか」というシミュレーションが簡単にできる
　2) 現実に対する「基準点」として機能する

1)の点は今回のnoteで行ったことです．接触というメカニズムを抽出してモデル化し，もし途中で接触が減ったらどうなるか，というシミュレーションを行いました．実際の社会ではそのような実験はまずできません．数理モデルであれば，いくらでもできます．

2)の点は，現実とモデルとのズレに焦点を当てています．たいてい，今回のような数理モデルは現実とズレます．だからモデルは役立たずなのか，というとそうではなく，そこから「なぜズレたのか」を考えていくことが重要になります．今回の場合ならモデルよりも現実が多いほうにズレたのであれば「接触以外にも感染経路があるんじゃないか」，あるいは現実のほうが少ないのであれば「普段から行っている何かが実は画期的な感染対策になっていたのではないか」と考えることができます．このように，モデルには現実との対比を行う上での参照点としての機能を持ちます．（2)の考え方は，モデルを改善するためにも活かせます．）

補足2：微分方程式

このSIRモデルは本来，微分方程式で表現されています．微分方程式とは日数のように離散的ではなく，連続的な時間の中で増減を扱うことができる枠組みです．具体的には以下の式で表現されます．

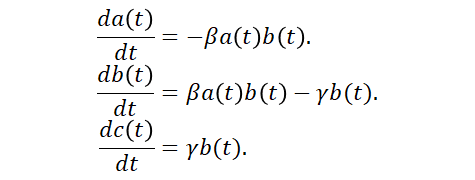
しかし，基本的な展開はこのnoteで扱ったことと同じです．もし，微分方程式の扱いに興味がある方は，冒頭にあげた参考文献を参照してください．また，参考文献にはSIRモデルのバリエーションも紹介されています．