初心者目線の確率過程入門

「確率過程」をご存知でしょうか？確率変数の連続データ版みたいなもので言語モデル、時系列解析のみならず株価など日常生活ですら結構見かける概念なのですがその単語自体出てこない確率論の教科書もざらです。また、確率過程自体をテーマとした書籍は確率論の書籍の中では少ないようです。一方で確率過程を前提としているテーマを扱っている書籍は結構多いのですが説明をあまりしない、もしくはわかっている前提で特に触れない書籍が多いのも実状です。

個人的には事前に確率過程の概念を簡単にでも整理しておけばこのテーマはスムーズに入っていけるな、と思うことが結構あります。

そこで入門レベルの内容ですが、確率過程について自分なりに調べた結果が誰かの役に立てばと思い、公開します。

確率過程の概要

・確率過程(stochastic process)とは確率の概念に時間変化を加えたもののこと。
・時間$${t(t_0,t_1,t_2,t_3,…)}$$ごとにそのパラメータ（正規分布なら平均や標準偏差）が変化する確率変数$${X(t)}$$が並んだ、
$${ \{ X(t) \} =X(t_0),X(t_1),X(t_2),X(t_3),... }$$
のこと。
・単一の確率変数同様に実現値を生成するが確率過程の場合、実現値は列をなす。
・別名として不規則過程(random process)、データ生成過程(Data Generating Process、DGP)とも呼ばれる。

(通常の)確率変数

・確率変数の実現値（標本を引いた結果）は単一の数値、状態など。
・個々の実現値は確率的に決まる。

コイン投げ

サイコロ

確率過程

・各時間ごとに確率変数を持つ。それらは互いに異なる確率分布に従う場合もあれば、同一な確率分布に従う場合もある。また独立な場合もあれば従属な場合もある。
・個々の確率変数の確率分布は様々（一様分布、ガウス分布など）
・確率過程の実現値を
　・データパス
　・サンプルパス
　・標本過程
　・見本過程
　・経路
　・パス
　・軌跡(軌道、trajectory)
　などと呼ぶ。
・金融、制御工学など確率過程が土台となる分野は多岐にわたる。

株価などある確率過程から得られた実現値の例（各色ごとの折れ線グラフ）。
確率変数の実現値のように標本を得るたびに異なる結果になるのが普通。

状態遷移を出力する確率過程もあり得る。状態B→状態C→状態Aや状態B→状態A→状態Cなど。やはりどのような状態遷移となるかは標本を取るたびに変わる。

確率過程における性質

定常性

・確率過程の実現値の時間や位置によって確率分布が変化しない確率過程は定常性を持つと言う。
・例えば時間$${t}$$に関係なく一定の平均、標準偏差に従う正規分布に従う各確率変数がからなる確率過程であるならばそれは定常性を持つ確率過程（定常性を持つガウス過程）となる。
・定常性を持つ確率過程を定常過程と呼ぶ。逆に定常過程ではない確率過程を非定常過程と呼ぶ。

例
・ホワイトノイズ（白色雑音）
下図は各時点でパラメータが同一（平均0、分散1）のガウス分布からなるガウス過程から生じているホワイトガウスノイズ（白色ガウス雑音）。

ホワイトノイズ（白色ガウス雑音）

マルコフ性

・次の時刻での確率分布が直前のn個の時刻での値によってのみ決まる性質をマルコフ性と呼び下記式で表す。マルコフ性をもつ確率過程をマルコフ過程と呼ぶ。
$${P_r(X_n+1=x|X_n=x_n,…,X_1=x_1,X_0=x_0)}$$
$${    =P_r(X_n+1=x|X_n=x_n)}$$
・未来を予測する際に、現在の情報以外のいかなる過去の情報も必要としない、みたいな説明でまず？？となるのがマルコフ性の典型的な説明です。しかし難しいことは言っておらず具体例を交えればわかり易いと思います。
　n=1の例（直前の過去のみ考慮するケース。単純マルコフ性と呼ばれる）として、下図の状態遷移図を考えましょう。矢印に添えられている数字は遷移確率（ある状態から別の状態に遷移する確率）を示しているとします。
　ここで、状態Cから状態Dへの遷移が起こった事実に対し、直前の状態が状態Cだったことだけが関係し、状態Cの前に状態Aであったかあるいは状態Bであったかは全く関係がない、というのがマルコフ性という性質です。要するに単純化してその確率過程を議論できる性質、ということです。

・ただ 1 つの状態から次に起こる事象が決定されるマルコフ過程を単純マルコフ過程と呼ぶ。
・連続する n個の状態系列から次に起こる事象が決定されるマルコフ過程をn階マルコフ過程またはn重マルコフ過程と呼ぶ。
・確率変数が離散値を取るマルコフ過程を特にマルコフ連鎖と呼ぶ。マルコフ連鎖は時間が離散的なものを指すことが多い。
・マルコフ性があると扱うモデルをシンプルできる利点がある。例えばある時系列データにおいて、それが単純マルコフ過程に従うものだとすれば次の値を予測する場合に直前の値だけを考慮すれば十分に予測できることになります。逆にマルコフ性がなくいくつも過去を遡らないと妥当な予測ができないとすれば予測は困難になるでしょう。
・マルコフ過程の発展型として、隠れマルコフ過程やマルコフ決定過程がある。

代表的な確率過程

ベルヌーイ過程

・ベルヌーイ試行（コイン投げなど）を繰り返したときに得られる結果を並べたもの。
・離散時間確率過程である。

ガウス過程

・正規確率過程とも呼ばれる。
・各時点での確率変数は正規分布に従う。
・一般に各時点での確率変数のパラメータ（平均、標準偏差）はことなり、それぞれも時間tに関数となることが一般的である。ただし前述のホワイトガウスノイズのように定常な場合は平均も標準偏差も時間tの関数ではなく固定ということにある。

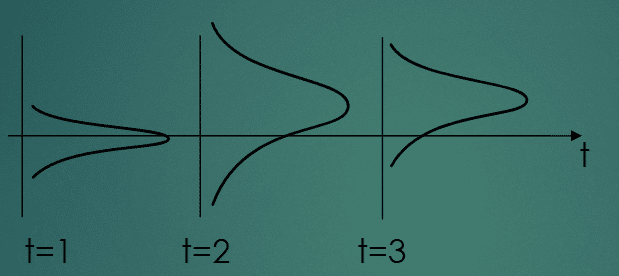
・上記は離散時間ガウス過程（時点は３つ）だが連続時間ガウス過程も存在する。
・ガウス過程の応用例はガウス過程回帰が挙げられる。
　各データに対する回帰分析を行う際、誤差がなるべく小さくなるように多項式などを当てはめるのではなく、ガウス過程を当てはめる平均、標準偏差を示す関数をフィッティングさせる。各点ごとのガウス分布の分散が信頼度となり、柔軟な予測を実現できる。
出典：
https://statmodeling.hatenablog.com/entry/how-to-use-GPy

ランダム・ウォーク

別名：酔歩、乱歩
・独立かつ同分布な確率変数 (Xn)の総和Snのこと。総和をSnとすると、
例えば、コインを投げて表が出れば+１，裏が出れば-1という足し算を繰り返していく。
・離散時間確率過程である。
・ある時刻でのSnは直前のSn-1にのみ依存、すなわち単純マルコフ連鎖である。
・金融理論では株価などはランダム・ウォークに従っており予測不可である、とするランダム・ウォーク理論（効率的市場仮説）がある。

ランダムウォークの例

ウィーナー過程

・ブラウン運動とも呼ばれる。
・ランダム・ウォークの連続時間型のこと。
・植物学者ロバート・ブラウンが、水中に流出し浮遊した微粒子の振る舞いを発見したことからその名がついた。
・ノーバート・ウィーナーにより数学的に解析されウィーナー過程とも
　呼ばれるようになった。

その他

その他の有名な確率過程として二項過程、ポワソン過程などがある。

参考文献

新インターユニバーシティ 確率と確率過程　武田一哉編著 オーム社
https://www.ohmsha.co.jp/book/9784274209307/
自然科学の統計学　東京大学教養学部統計学教室 編
http://www.utp.or.jp/book/b300859.html
「確率過程とその応用」 　逆瀬川浩孝　早稲田大学の学内資料？
http://www.f.waseda.jp/sakas/stochastics/
確率過程（ウィキペディア）

確率過程 - Wikipedia