Pythonで学ぶ統計学4:推測統計(推定)
1.概要
本記事は統計学の学習記録用として作成しており、私が理解するのに時間がかかった場所や追って参照したい内容を中心にまとめております。
本記事のテーマは「推測統計:推定」になります。
参考資料として下記(CC-BY)を使用させていただきました。
1-1.記事説明:データとPythonライブラリ
本記事で使用したサンプルデータを紹介します。本題ではないため詳細な説明は省きます。
またPythonも使用していきますがライブラリの詳細説明は省きますので個別のライブラリは別記事で確認お願いします。なおScipyは(2023年1月現在)では記事を作成しておりませんがこちらも説明は省きます。
2.推定の用語
推定で使用する用語一覧を事前に記載しておきます。
母数:母平均や母分散など、母集団が持つ固有の統計量のこと
母比率:母集団の比率(母集団内の相対度数)
標本比率:標本内の比率(標本内の相対度数)
自由度:自由に値を取れるデータの数のこと。不偏分散の計算ではサンプル数n-1を自由度として用いる
統計量:データの特徴を要約した数値
点推定:推定方法の1つであり、平均値などを1つの値で推定
区間推定:推定方法の1つであり、平均値などをある区間でもって推定
標準誤差:点推定において、推定量がどのくらい正しいものかを表す指標であり、標本から得られる推定量そのもののバラつきを表す
(95%)信頼区間(confidence interval, CI):母集団から標本を取ってきて、その平均から95%信頼区間を求める、という作業を100回やったときに、95回はその区間の中に母平均が含まれるという"頻度"もしくは"割合"(確率ではない)
推測統計:母集団から抽出した標本の情報を用いて、母集団の情報を推測する。統計学的に推測するには、データに当てはまるであろう確率分布を推定し、その確率分布を基に、母集団のデータを推測します。
大数の法則(law of large numbers):ある独立した試行においてその事象が発生する確率をpとすると、試行回数nが大きくなるにつれて事象の発生確率がpに近づいていくこと
中心極限定理:母集団が正規分布でなくても、そこから抽出したサンプルサイズNが大きくなると標本の分布は正規分布に近づく
標準誤差(SE:standard error):標本から測定された統計量の標準偏差であり標本統計量の精度を表す。標本平均の標準偏差を指すことが多い
$$
標準誤差(SE):\sqrt{\frac{分散}{サンプル数}}=\sqrt{\frac{\sigma^2}{n}}=\frac{\sigma}{\sqrt{n}}
$$


3.推測統計とは
3-1.記述統計と推測統計の違い
統計学には記述統計と推測統計があり、特徴は下記の通りです。
【記述統計(Descriptive Statistics):提唱者 カールピアソン】
取得したデータを整理・集約して、そのデータが表す性質を定数として表現する。
【推測統計(Inferential Statistics):提唱者 ロナルドフィッシャー】
取得したデータを整理・集約して、そのデータが表す性質を確率として表現する。つまり見えるデータ(標本)から求めたい未知データ(母集団)を分布として推測する手法です。
推測統計は大きく分けて「推定問題」と「検定問題」があります。本記事では推定を紹介しますが「基本的な考え方・計算する統計量は検定・推定とも同じ」です。
推定:標本データから母集団の統計量(母平均や母分散)を推定する。推定には信頼区間を用いて確率で計算する。
検定:母集団に関するある仮説が統計学的に成り立つか否かを、標本のデータを用いて判断すること
【コラム:ピアソンとフィッシャーについて】
各種統計学を体系化した両氏ですが、統計学だけでなく様々なことを提案しており今でも重要な内容ばかりとなります。
【カールピアソン】
線形回帰、相関とピアソンの積率相関係数:彼はゴルトンによる「平均回帰」データを用いて数学モデルを構成し、以後これらの理論の発展に中心的役割を演じた。
ピアソンのカイ二乗検定:カイ二乗検定のうち最も基本的なものである。
ヒストグラム:用語を創案した。
【ロナルドフィッシャー】
実験計画法・分散分析・小標本の統計理論
集団遺伝学の創始者
分散分析(ANOVA, Analysis of variance)の基本的手法を確立
最尤法という手法を確立
3-2.推定の種類:点推定と区間推定
記述統計ではデータを定数として扱いましたが、母集団から標本を抽出すると標本には分布が発生します。
その分布を考慮して推定には「点推定」と「区間推定」があります。
【点推定】
母集団の平均や分散などの特性値を1つの値(定数)で表現する。
(※記述統計と似ているが分散の数式などが異なる。標本抽出時のばらつきを考慮してサンプルサイズnではなく自由度n-1を使用する)
【区間推定】
母集団の分布を仮定したうえで、標本データを用いて母平均などの推定量を、1つの値ではなく、確率的な区間(幅)で表現する(例:母数がある区間に入る確率はX%以上)
※推定するのは母数(母平均や母分散)であり母集団の分布は求めません。
3-3.標本分散と不偏分散
標本のデータから(標本)分散を計算すると、標本抽出による誤差の影響で過小評価されます。
$$
母分散 = 標本分散+標本平均のばらつき
$$
母集団の分散を適切に推定するために不偏分散を使用します。計算としてはサンプル数を通常の分散(標本分散)より1小さくします。
$$
標本分散\sigma^2 = \frac{1}{n}\displaystyle \sum_{ i = 1 }^{ n } (x_i-\overline{x})^2
$$
$$
不偏分散\sigma^2 = \frac{1}{n-1}\displaystyle \sum_{ i = 1 }^{ n } (x_i-\overline{x})^2
$$
デフォルトとして「Numpy:標本分散、Pandas:不偏分散」の値が出力されます。Numpyで不偏分散を計算する場合は引数"ddof=1"とします。
[IN]
x = np.random.randn(100)
mean, var, std = x.mean(), x.var(), x.std()
print(f'Numpy 平均:{mean:.3f}, 分散: {var:.3f}, 標準偏差: {std:.3f}')
mean, var, std = x.mean(), x.var(ddof=1), x.std(ddof=1)
print(f'Numpy 平均:{mean:.3f}, 分散: {var:.3f}, 標準偏差: {std:.3f}')
df_x = pd.DataFrame(x, columns=['x'])
mean, var, std = df_x['x'].mean(), df_x['x'].var(), df_x['x'].std()
print(f'Pandas 平均:{mean:.3f}, 分散: {var:.3f}, 標準偏差: {std:.3f}')
[OUT]
Numpy 平均:0.027, 分散: 1.273, 標準偏差: 1.128
Numpy 平均:0.027, 分散: 1.286, 標準偏差: 1.134
Pandas 平均:0.027, 分散: 1.286, 標準偏差: 1.1344.推測統計のポイント
4-1.推定の目的
下記記事で記載した通り、母集団と標本には下記の関係があります。
無作為抽出しても全数でなければ「母集団」≠「標本」である。
母集団から複数のサンプルを取得した時、統計量(平均・分散)は各標本で異なる(標本に分布が発生する)。
一般的に(時間・コストのため)得られるデータは標本だが、ほしいデータは母集団である。
上記より推定の目的は「標本から母集団を推測したい」ことにあります。母集団の分布は推定が難しい※ため、「標本から母集団の平均、分散、母比率のみを推定」します。
※母集団の分布は不明のため特定の確率分布に従うと仮定して推定します。このように、母集団分布に特定の分布を仮定した検定のことを「パラメトリック検定」と言います。
4-2.点推定
点推定では標本から母集団の特性値(平均値、分散)を定数で推測するため記述統計と似ておりますが分散は不偏分散となります。
なお点推定では標本の分布を考慮できないため次の区間推定の方が重要になります。
$$
\begin{aligned} 平均値\overline{x} = \frac{x_1 + x_2 + \dots + x_N}{N} = \frac{1}{N} \sum^{N}_{n=1} x_{n} \end{aligned}
$$
$$
不偏分散\sigma^2 = \frac{1}{n-1}\sum_{i=1}^{n} (x_i - \bar{x})^2
$$
推定量がどのくらい正しいものかを表す指標に標準誤差があります。標準誤差は推定量の標準偏差であり、標本から得られる推定量そのもののバラつきを表すものです。
$$
標準誤差=\frac{\sigma}{\sqrt{n}}=\frac{\sqrt{不偏分散}}{\sqrt{n}}=\frac{\sqrt{ \frac{1}{n-1}\sum_{i=1}^{n} (x_i - \bar{x})^2}}{\sqrt{n}}
$$
例として後述しますが、母集団が正規分布に従い母分散が既知である場合は統計量z(z値)を使用します。下記数式の通り、z値の分母は標準誤差であり標準誤差が小さくなるとz値が大きくなり統計的に確率が増加します。
$$
−1.96≦z=\frac{\bar x – μ}{\sqrt{\frac {σ^2}{n}}}≦1.96 (95%信頼区間)
$$
$$
\bar{x} –1.96 \sqrt{\frac {σ^2}{n}} \le μ \le \bar{x} + 1.96\sqrt{\frac {σ^2}{n}}
$$

4-3.区間推定の考え方
区間推定は母数(平均値$${\mu}$$や標準偏差$${\sigma}$$)がある区間に入る確率をX%以上になるように保証する推定方法となります。
4-3-1.確率分布における確率
各種確率分布は数式で表され標準偏差σ内における確率は計算できます。正規分布ではμ±σ内に95%の確率でデータが分布します。

【標準正規分布のμ±σの積分を確認】
Sympyを使用して標準正規分布(平均0, 標準偏差1)におけるμ±σ内が95%になることを確認してみました。
[IN]
import sympy as sym
sym.init_printing(True)
def normal_dist(x, mu, sigma):
return 1/(sigma*sym.sqrt(2*sym.pi))*sym.exp(-(x-mu)**2/(2*sigma**2))
x, mu, sigma = sym.symbols('x μ σ')
math_normal = normal_dist(x, mu, sigma)
display(math_normal)
math_stdnormal = normal_dist(x, 0, 1)
display(math_stdnormal)
result = sym.integrate(math_stdnormal, (x, -1.96, 1.96))
result.evalf()
[OUT]
0.950004209703559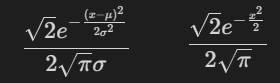
【正規分布の標準偏差と信頼区間の可視化】
正規分布、可視化、信頼区間(累積密度分布)はそれぞれNumpy, Matplotlib, Scipyで実装できます。Scipyの出力は下記に注意が必要です。
信頼水準の値は小数単位で入力
引数xに信頼水準を渡すとタプルで両側の値が得られる。つまり95%信頼区間の場合(下2.5%、上2.5%)が出力
下側の出力値はマイナス値も出る。出力値を加算計算する場合は注意
[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
from scipy import stats
x = np.arange(-5, 5, 0.01)
mean, std = 0, 1
y = stats.norm.pdf(x, loc=mean, scale=std) #正規分布
z_low95, z_up95 = stats.norm.interval(0.95, loc=mean, scale=std) #標準正規分布の信頼区間(累積分布関数)
z_low99, z_up99 = stats.norm.interval(0.99, loc=mean, scale=std) #標準正規分布の信頼区間(累積分布関数)
fig, ax = plt.subplots(figsize=(10, 6), facecolor='w')
ax.plot(x, y, label='標準正規分布', color='red')
ax.vlines([std, std], 0, stats.norm.pdf(std, loc=mean, scale=std),
colors='red', linestyle='--', lw=1, label='1σ')
ax.vlines([-std, -std], 0, stats.norm.pdf(-std, loc=mean, scale=std),
colors='red', linestyle='--', lw=1, label='1σ')
ax.vlines([2*std, 2*std], 0, stats.norm.pdf(2*std, loc=mean, scale=std),
colors='blue', linestyle='-.', lw=1, label='2σ')
ax.vlines([-2*std, -2*std], 0, stats.norm.pdf(-2*std, loc=mean, scale=std),
colors='blue', linestyle='-.', lw=1, label='2σ')
#95%信頼区間外を塗りつぶし
ax.fill_between(x, y, where=(x < z_low95) | (x > z_up95),
color='red', alpha=0.3, label='95%信頼区間')
ax.fill_between(x, y, where=(x < z_low99) | (x > z_up99),
color='blue', alpha=0.3, label='99%信頼区間')
ax.set(xlabel='x', ylabel='確率密度', xticks=np.arange(-5, 5+1, 1))
plt.legend(), plt.grid()
plt.show()
[OUT]
4-3-2.信頼水準・信頼区間
標本を抽出すると、各抽出の標本平均にはばらつきが発生します。つまり、標本平均にも分布が存在します。
(くどいですが、真値は変動せず、ばらつくのはデータや推定値です。)
【信頼水準(Confidence level)】
追って
【信頼区間(Confidence interval, CI)】
統計学で母集団の真値(母平均等)が含まれることが確信 (confident) できる数値範囲のこと。
95%信頼区間を設定した場合、「同様の標本抽出を100回行えば95回はその中に母平均μを含む」ことが言えます。重要なこととして「信頼区間内に母集団がいる確率ではなく、同様の抽出を実施した時に区間内に母平均が入らない確率」であることに注意が必要です。

4-3-3.検定統計量
区間推定では母集団の母数を推定するために標本データを用いて検定統計量という指標を計算します。
例として母集団の分布が正規分布で母分散既知の場合は統計量z値が使用されます。95%信頼区間では(正規分布同様に)z値は下記の通りとなります。
$$
-1.96≦Z≦1.96(95%の信頼水準)※99%だと-2.58≦Z≦2.58
$$
$$
-1.96≦\frac{\bar x – μ}{\sqrt{\frac {σ^2}{n}}}≦1.96
$$

上記より求めたい母平均は下記の通り計算でき、母平均はある区間において指定した確率内に存在することを推定できます。
$$
\bar{x} –1.96 \sqrt{\frac {σ^2}{n}} \le μ \le \bar{x} + 1.96\sqrt{\frac {σ^2}{n}}
$$
4-3-4.試験による可視化1:信頼区間
信頼区間は理解しにくいためPythonコードでサンプルを作成しました。今回のサンプルは下記の通りです。
正解用(母集団)としてrandn()で正規分布に従う乱数値を生成
標本として標本1=(μ:0, σ:1)、標本2=(μ:0.5, σ:1)、標本3=(μ:-1, σ:1)を3個ずつ作成(計9個)。
標本のサンプルサイズはばらつきが出るように小さめ(n=7)に設定
まず初めに信頼区間ではなく、データの平均とばらつきを箱ひげ図を用いて可視化しました。箱ひげ図の中心線は平均値μではなく中央値のため別途μのマーカーを追加しました。
[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
from scipy import stats
import glob
import os
np.random.seed(123)
#母集団
nums = int(1e6)
y = np.random.randn(nums) #標準正規分布に従う乱数を大量に生成(母集団)
freqs, _x = np.histogram(y, bins=100) #ヒストグラムを作成
probs = freqs / nums #確率密度を計算
x = (_x[1:] + _x[:-1]) / 2 #x軸の値を計算
#標本を作成
mean, std = 0, 1
nums_sample = 7
s1_u0 = np.random.normal(mean, std, size=nums_sample)
s2_u0 = np.random.normal(mean, std, size=nums_sample)
s3_u0 = np.random.normal(mean, std, size=nums_sample)
s1_u05 = np.random.normal(0.5, std, size=nums_sample)
s2_u05 = np.random.normal(0.5, std, size=nums_sample)
s3_u05 = np.random.normal(0.5, std, size=nums_sample)
s1_u1 = np.random.normal(-1, std, size=nums_sample)
s2_u1 = np.random.normal(-1, std, size=nums_sample)
s3_u1 = np.random.normal(-1, std, size=nums_sample)
#平均値を計算
mean1_u0, mean2_u0, mean3_u0 = s1_u0.mean(), s2_u0.mean(), s3_u0.mean()
mean1_u05, mean2_u05, mean3_u05 = s1_u05.mean(), s2_u05.mean(), s3_u05.mean()
mean1_u1, mean2_u1, mean3_u1 = s1_u1.mean(), s2_u1.mean(), s3_u1.mean()
#信頼区間を計算
lim_low1_u0, lim_high1_u0 = mean1_u0-1.96*std/np.sqrt(nums_sample), mean1_u0+1.96*std/np.sqrt(nums_sample)
lim_low2_u0, lim_high2_u0 = mean2_u0-1.96*std/np.sqrt(nums_sample), mean2_u0+1.96*std/np.sqrt(nums_sample)
lim_low3_u0, lim_high3_u0 = mean3_u0-1.96*std/np.sqrt(nums_sample), mean3_u0+1.96*std/np.sqrt(nums_sample)
lim_low1_u05, lim_high1_u05 = mean1_u05-1.96*std/np.sqrt(nums_sample), mean1_u05+1.96*std/np.sqrt(nums_sample)
lim_low2_u05, lim_high2_u05 = mean2_u05-1.96*std/np.sqrt(nums_sample), mean2_u05+1.96*std/np.sqrt(nums_sample)
lim_low3_u05, lim_high3_u05 = mean3_u05-1.96*std/np.sqrt(nums_sample), mean3_u05+1.96*std/np.sqrt(nums_sample)
lim_low1_u1, lim_high1_u1 = mean1_u1-1.96*std/np.sqrt(nums_sample), mean1_u1+1.96*std/np.sqrt(nums_sample)
lim_low2_u1, lim_high2_u1 = mean2_u1-1.96*std/np.sqrt(nums_sample), mean2_u1+1.96*std/np.sqrt(nums_sample)
lim_low3_u1, lim_high3_u1 = mean3_u1-1.96*std/np.sqrt(nums_sample), mean3_u1+1.96*std/np.sqrt(nums_sample)
print(f'μ_標本1-1:{mean1_u0:.2f}, μ_標本1-2:{mean2_u0:.2f}, μ_標本1-3:{mean3_u0:.2f}')
print(f'μ_標本2-1:{mean1_u05:.2f}, μ_標本2-2:{mean2_u05:.2f}, μ_標本2-3:{mean3_u05:.2f}')
print(f'μ_標本3-1:{mean1_u1:.2f}, μ_標本3-2:{mean2_u1:.2f}, μ_標本3-3:{mean3_u1:.2f}')
print(f'区間推定 標本1-1:{lim_low1_u0:.2f}≦ μ ≦{lim_high1_u0:.2f}, 標本1-2:{lim_low2_u0:.2f}≦ μ ≦{lim_high2_u0:.2f}, 標本1-3:{lim_low3_u0:.2f}≦ μ ≦{lim_high3_u0:.2f}')
print(f'区間推定 標本2-1:{lim_low1_u05:.2f}≦ μ ≦{lim_high1_u05:.2f}, 標本2-2:{lim_low2_u05:.2f}≦ μ ≦{lim_high2_u05:.2f}, 標本2-3:{lim_low3_u05:.2f}≦ μ ≦{lim_high3_u05:.2f}')
print(f'区間推定 標本3-1:{lim_low1_u1:.2f}≦ μ ≦{lim_high1_u1:.2f}, 標本3-2:{lim_low2_u1:.2f}≦ μ ≦{lim_high2_u1:.2f}, 標本3-3:{lim_low3_u1:.2f}≦ μ ≦{lim_high3_u1:.2f}')
#箱ひげ図で可視化
fig, ax = plt.subplots(figsize=(12, 6), facecolor='w')
datas = [y, s1_u0, s2_u0, s3_u0, s1_u05, s2_u05, s3_u05, s1_u1, s2_u1, s3_u1]
labels = ['母集団(正規分布)', '標本1-1', '標本1-2', '標本1-3', '標本2-1', '標本2-2', '標本2-3', '標本3-1', '標本3-2', '標本3-3']
colors = ['red', 'blue', 'blue', 'blue', 'green', 'green', 'green', 'orange', 'orange', 'orange']
bp=ax.boxplot(datas, labels=labels,
sym="", #sym=""で外れ値を表示しない
showmeans=True, #平均値を表示
patch_artist=True, #TrueにしないとfacecolorがError
vert=False)
#Boxの色を変更
for b, c in zip(bp['boxes'], colors):
b.set(color='black', linewidth=1) #boxの外枠の色
b.set_facecolor(c) #boxの色
ax.plot([mean, mean], [0, len(datas)], color='red', linestyle='--') #母集団の平均値を破線で表示
ax.set(title='箱ひげ図', xlabel='値', ylabel='標本')
[OUT]
μ_標本1-1:0.16, μ_標本1-2:-0.37, μ_標本1-3:-0.24
μ_標本2-1:0.61, μ_標本2-2:0.43, μ_標本2-3:0.64
μ_標本3-1:-1.13, μ_標本3-2:-1.34, μ_標本3-3:-1.06
区間推定 標本1-1:-0.58≦ μ ≦0.90, 標本1-2:-1.11≦ μ ≦0.37, 標本1-3:-0.98≦ μ ≦0.50
区間推定 標本2-1:-0.13≦ μ ≦1.35, 標本2-2:-0.31≦ μ ≦1.17, 標本2-3:-0.10≦ μ ≦1.38
区間推定 標本3-1:-1.87≦ μ ≦-0.39, 標本3-2:-2.08≦ μ ≦-0.60, 標本3-3:-1.80≦ μ ≦-0.32

上記より「各標本の平均値は同じ条件でもばらつきがある。また真値が正しい標本(青)と異なる標本(緑)で似たようなばらつきがみえる」ことが分かります。
この時「各標本の標本平均は母平均と同じか?」という判断をするために区間推定が必要となります。結果から下記が確認できます。
(同じ条件で無作為抽出しても)各標本で信頼区間は変化する。よって標本のデータから母平均の真値は判断できない。
今回のケースだと標本1(真値と同じμ=0, σ=1)の信頼区間は100個作成したら5個は真値(μ=0)から外れる可能性がある。
標本した母集団の母平均が求めたい値(真値)と異なっていても、標本から作製した信頼区間に真値が入ることはある。ただこれは母平均そのものを説明しているわけではなく、ただの確率値である。
[IN]
lims_low = [lim_low1_u0, lim_low2_u0, lim_low3_u0,
lim_low1_u05, lim_low2_u05, lim_low3_u05,
lim_low1_u1, lim_low2_u1, lim_low3_u1]
lims_high = [lim_high1_u0, lim_high2_u0, lim_high3_u0,
lim_high1_u05, lim_high2_u05, lim_high3_u05,
lim_high1_u1, lim_high2_u1, lim_high3_u1]
fig, ax = plt.subplots(figsize=(12, 6), facecolor='w')
ax.vlines(0, 0, 1, color='red', linestyle='-', label='正規分布の平均')
for idx, (lim_low, lim_high) in enumerate(zip(lims_low, lims_high)):
idx += 1
y = idx * 0.1
if idx <= 3:
c = 'blue'
elif idx <= 6:
c = 'green'
else:
c = 'orangered'
ax.plot([lim_low, lim_high], [y, y],
color=c, linestyle='--', label=f'標本{idx}')
ax.set(xlabel='平均値μ', xticks=np.arange(-2, 2.1, 0.5))
ax.tick_params(labelleft=False) #y軸の目盛りを非表示
plt.title('区間推定', y=-0.18)
plt.legend(), plt.grid()
plt.show()
[OUT]
区間推定 標本1-1:-0.58≦ μ ≦0.90, 標本1-2:-1.11≦ μ ≦0.37, 標本1-3:-0.98≦ μ ≦0.50
区間推定 標本2-1:-0.13≦ μ ≦1.35, 標本2-2:-0.31≦ μ ≦1.17, 標本2-3:-0.10≦ μ ≦1.38
区間推定 標本3-1:-1.87≦ μ ≦-0.39, 標本3-2:-2.08≦ μ ≦-0.60, 標本3-3:-1.80≦ μ ≦-0.32
4-3-5.試験による可視化2:95%信頼区間の確率をシミュレーション
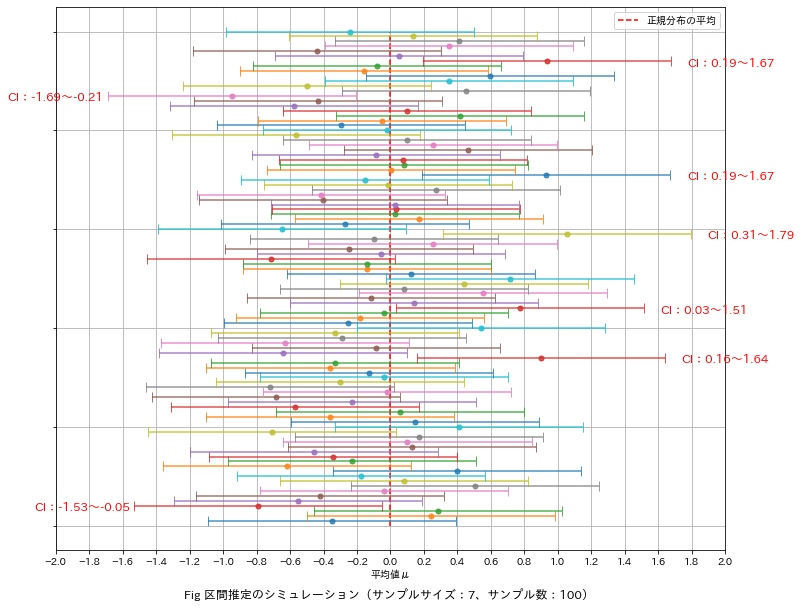
論より証拠で「正規分布を生成する乱数器を用いて、サンプルサイズn=7で標本を100個生成し各標本の信頼区間」が真値に対してどうなるか確認しました。結果は下記の通りです。
正規分布に従う乱数で生成しても95%信頼区間では100個中7個が真値から外れる」結果となりました。
今回は正規分布をベースに作成したため真値(母平均)はわかっておりますが通常の問題では真値の確認できない(あくまで区間を推定するだけ)。
ポイント1:「確からしい標本でも、標本抽出で信頼区間から外れる可能性がある」ことは注意が必要です。
ポイント2:ばらつきは$${\frac{\sigma}{\sqrt{n}}}$$で小さくなるため適切なサンプルサイズを設定することで精度を向上できます。
ポイント3:理論的にはばらつきがなければ(σ=0)標本平均=母平均(真値)となる。製造現場ではばらつきがある中で(見えない)真値がいくらかを検討するよりばらつきを抑える方に価値があると思う。
[IN]
np.random.seed(12)
mean, std = 0, 1 #母平均、母標準偏差
#サンプルサイズ7の標本を100個生成->標本平均分布に変換
mean, std = 0, 1 #母平均、母標準偏差
data_raw = np.random.normal(mean, std, size=(100, 7)) #標本抽出:標準正規分布、サンプルサイズ=7
data_mean = data_raw.mean(axis=1) #標本平均
print('標本:', np.array(datas_raw).shape, '標本平均:', np.array(datas_mean).shape)
#信頼区間の計算:x±1.96*σ/√n
lims_low = [i-1.96*std/np.sqrt(nums_sample) for i in datas_mean]
lims_high = [i+1.96*std/np.sqrt(nums_sample) for i in datas_mean]
#信頼区間外のデータを抽出
df = pd.DataFrame(np.array([lims_low, lims_high]).T, columns=['下限', '上限'])
df_out95CI = df.query('下限 >= 0 or 上限 <= 0') #母平均を含まない区間のみ抽出
display(df_out95CI.T)
#グラフ作成
fig, ax = plt.subplots(figsize=(12, 10), facecolor='w')
ax.vlines(0, 0, len(datas_raw)*0.1, color='red', linestyle='--', label='正規分布の平均')
for idx, (lim_low, lim_high) in enumerate(zip(lims_low, lims_high)):
idx += 1
y = idx * 0.1
ax.errorbar(datas_mean[idx-1], y, xerr=1.96*std/np.sqrt(nums_sample),
capsize=5, fmt='o', markersize=5, linestyle='-', lw=1.5, alpha=0.8)
#信頼区間外のデータを描写
for idx in df_out95CI.index:
data = df_out95CI.loc[idx]
if data['下限'] >= 0:
ax.text(data['上限']+0.1, idx*0.1,
f'CI:{data["下限"]:.2f}~{data["上限"]:.2f}', fontsize=12, color='red')
else:
ax.text(data['下限']-0.6, idx*0.1,
f'CI:{data["下限"]:.2f}~{data["上限"]:.2f}', fontsize=12, color='red')
ax.set(xlabel='平均値μ', xticks=np.arange(-2, 2.1, 0.2))
ax.tick_params(labelleft=False) #y軸の目盛りを非表示
plt.title(f'Fig 区間推定のシミュレーション(サンプルサイズ:{nums_sample}、サンプル数:{100}) ', y=-0.10)
plt.legend(), plt.grid()
plt.show()
[OUT]
標本: (100, 7) 標本平均: (100,)
5.信頼区間と統計量z値の深堀
信頼区間をさらに理解するためにもう一つシミュレーションをしました。条件は別記事で使用したものと同等にしています。
なお母集団は正規分布と仮定しており、本検証はパラメトリック検定となります。
【シミュレーションの条件:30-39歳の男性の身長】
●母集団の平均値、標準偏差、サンプル数:μ=172.1、σ=6.1, 全数=1000万
●標本サイズn=10, 100, 1000
●標本数=1(一つの標本から確率を推定する)
【推定の条件】
●推定の対象(未知の値):母平均※
●既知の条件:母分散※
※数値計算のため真値は上記の通りですが通常は知りえない値となります。
内容としては”標準化”、”正規分布”、”中心極限定理”、”標本平均の分布”を組み合わせれば理解できると思います。
[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import sympy as sym
from scipy import stats
np.random.seed(135)
class GetSample:
def __init__(self, mean_p, std_p, size_population):
self.mean_p = mean_p #母平均
self.std_p = std_p #母分散の標準偏差
self.size_population = size_population #標本サイズ
self.population = np.random.normal(self.mean_p, self.std_p, size_population) #母集団を作成
def sampling(self, sample_size, nums_sample):
output = [np.random.choice(self.population, sample_size, replace=False) for _ in range(nums_sample)] #replace=Falseで重複なし
return np.array(output)
#母集団の作成
mean, std, size_population = 172.1, 6.1, int(1e7)
data_p = GetSample(mean, std, size_population)
population = data_p.population
print(f'母数 n:{len(population)}, μ:{population.mean():.2f}, var:{population.var():.2f}, σ:{population.std():.2f}')
fig = plt.figure(figsize=(12, 8), facecolor='w')
plt.hist(population, bins=100, label='標本平均', density=False)
plt.vlines(mean, 0, 4.5e5, label='母平均μ', color='red', ls='--', lw=1)
plt.vlines(mean+std, 0, 3.0e5, label='母標準偏差σ', color='orangered', ls='--', lw=1)
plt.vlines(mean-std, 0, 3.0e5, color='orangered', ls='--', lw=1)
plt.yticks(np.arange(0, 5.5e5, 5e4))
plt.xticks(np.arange(145, 205, 5))
plt.xlim(145, 200)
plt.text(mean, 4.6e5, f'μ', ha='center', va='bottom', color='red', fontsize=15)
plt.text(mean+std/1.5, 4.6e5, f'σ:{std}', ha='center', va='bottom', color='orangered', fontsize=15)
plt.text(mean-std/1.5, 4.6e5, f'σ:{std}', ha='center', va='bottom', color='orangered', fontsize=15)
#μとσの間に矢印を描画
plt.annotate('', xy=(mean-1, 4.6e5), xytext=(mean-std, 4.6e5), arrowprops=dict(arrowstyle='<->', color='orangered'))
plt.annotate('', xy=(mean+std, 4.6e5), xytext=(mean+1, 4.6e5), arrowprops=dict(arrowstyle='<->', color='orangered'))
plt.ylim(0, 5.0e5)
plt.legend(loc='upper right'), plt.grid()
plt.show()
[OUT]
母数 n:10000000, μ:172.10, var:37.18, σ:6.10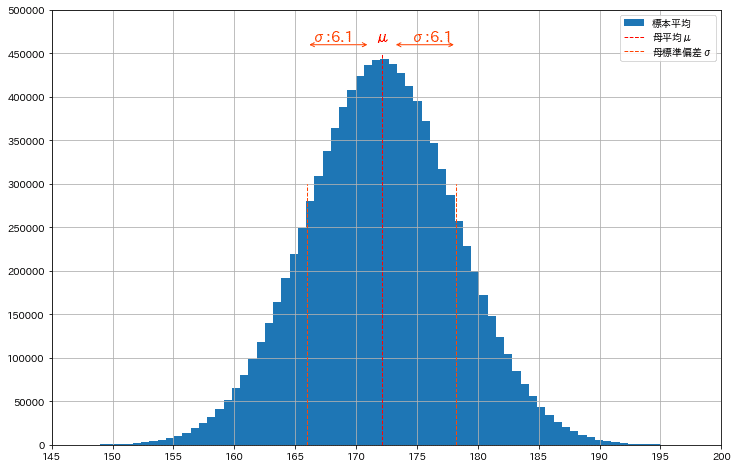
5-1.標準化と標準正規分布
標準化とは「平均値$${\mu}$$:0, 標準偏差$${\sigma}$$:1にする処理」のことです。正規分布に従うデータを標準化したものを標準正規分布と呼びます。
$$
標準化(z値)=\frac{データ-平均値}{標準偏差}=\frac{x-\mu}{\sigma}
$$
$$
正規分布\mathcal{N}(\mu, \sigma^2)=\dfrac{1}{\sqrt{2\pi\sigma}}\exp(-\dfrac{(x-\mu)^ 2}{2\sigma^ 2})
$$
$$
標準正規分布\mathcal{N}(0, 1)=\dfrac{1}{\sqrt{2\pi}}\exp(-\dfrac{x^ 2}{2})
$$
処理のイメージとしては下記の通りです。
データ全体を$${\mu}$$分だけスライド($${\mu}$$を引き算)する。データの重心は$${\mu}$$分だけずれるため、スライド後の平均値は0になる。
データ全体を$${\sigma}$$分だけ圧縮($${\sigma}$$で割り算)する。データを拡張/圧縮する(x軸が変わる)ため、確率密度も変化する。
[IN]
def make_plot(ax, x, y, label, title):
ax.plot(x, y, label=label)
ax.set(xlabel='x', ylabel='確率密度')
ax.set_title(title, y=-0.15)
ax.legend()
ax.grid()
p_dense_population, bins = np.histogram(population, bins=100, density=True)
_x = bins[:-1] -mean #平均値を0にする
x_scale = _x/std #標準偏差を1にする
p_dense_scale, bins_scaled = np.histogram((population-mean)/std, bins=100, density=True)
#可視化
fig, axs = plt.subplots(1, 3, figsize=(14, 6), facecolor='w')
axs = axs.ravel()
make_plot(axs[0], bins[:-1], p_dense_population, 'x', '母集団')
make_plot(axs[1], _x, p_dense_population, 'x-μ', '平均値μを引き平均値を0にする')
make_plot(axs[2], x_scale, p_dense_scale, '(x-μ)/σ', 'σで割り標準偏差を1にする')
[OUT]
なお標準正規分布は確率密度関数のため関数の定積分=確率となります。
[IN]
x = np.linspace(-4, 4, 100)
y = stats.norm.pdf(x, 0, 1)
#標準正規分布の確率
sigma = 1
p_1sigma = stats.norm.cdf(sigma*1)-stats.norm.cdf(-sigma*1)
p_2sigma = stats.norm.cdf(sigma*2)-stats.norm.cdf(-sigma*2)
p_3sigma = stats.norm.cdf(sigma*3)-stats.norm.cdf(-sigma*3)
print(f'-σ~σの確率:{p_1sigma:.3f}, -2σ~2σの確率:{p_2sigma:.3f}, -3σ~3σの確率:{p_3sigma:.3f}')
fig = plt.figure(figsize=(12, 8), facecolor='w')
plt.plot(x, y, label='標準正規分布')
plt.fill_between(x, y, where=(x>=-1*sigma)&(x<=1*sigma), color='red', alpha=0.3, label=f'-σ~σの確率:{p_1sigma:.3f}')
plt.fill_between(x, y, where=(x>=-2*sigma)&(x<=2*sigma), color='orangered', alpha=0.3, label=f'-2σ~2σの確率:{p_2sigma:.3f}')
plt.fill_between(x, y, where=(x>=-3*sigma)&(x<=3*sigma), color='orange', alpha=0.3, label=f'-3σ~3σの確率:{p_3sigma:.3f}')
plt.text(0, 0.30, f'-σ~σ:p={p_1sigma:.3f}', ha='center', va='bottom', color='red', fontsize=15)
plt.text(0, 0.25, f'-2σ~2σ:p={p_2sigma:.3f}', ha='center', va='bottom', color='blue', fontsize=15)
plt.text(0, 0.20, f'-3σ~3σ:p={p_3sigma:.3f}', ha='center', va='bottom', color='green', fontsize=15)
plt.legend(loc='upper right'), plt.grid()
plt.show()
[OUT]
-σ~σの確率:0.683, -2σ~2σの確率:0.954, -3σ~3σの確率:0.997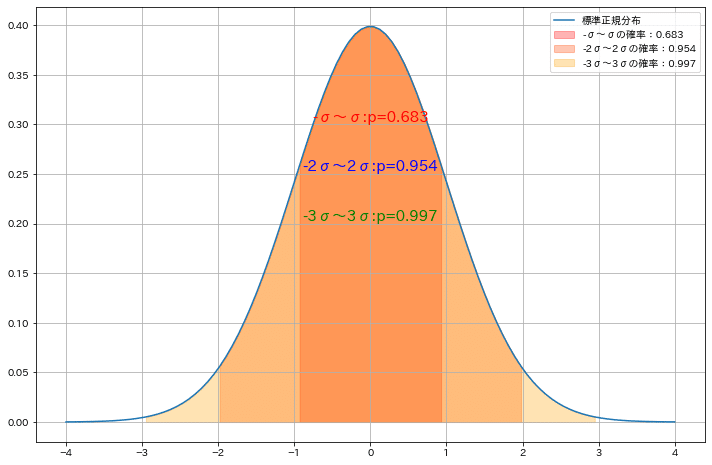
5-2.標本平均の分布と中心極限定理
標本抽出をすると標本平均を計算できますが、この標本平均は抽出ごとに変化するため分布が存在します。中心極限定理より「標本数nが大きくなれば標本平均の分布の平均値は母平均$${\mu}$$、分散は$${\frac{\sigma^2}{n}}$$の正規分布に近づく」ことが分かっています(※$${\sigma^2}$$は標本分散ではなく母分散)。
下記に母集団から標本数n=10, 100, 1000でサンプリングした標本の統計量と標準誤差を計算しました。
重要なこととして「標本数nが大きいと標本内での分散は大きくなりますが、中心極限定理より標本平均の分布は正規分布となり分散は小さくなる」ことを頭に入れておく必要があります。
[IN]
np.set_printoptions(precision=2) #小数点以下2桁
#標本抽出
nums_sample = 1 #サンプル数
sample_size10 = 10 #サンプルサイズ,
sample_size100 = 100 #サンプルサイズ, サンプル数
sample_size1000 = 1000 #サンプルサイズ, サンプル数
sample10 = data_p.sampling(sample_size10, nums_sample) #標本抽出:サンプルサイズ10、サンプル数1
sample100 = data_p.sampling(sample_size100, nums_sample) #標本抽出:サンプルサイズ100、サンプル数1
sample1000 = data_p.sampling(sample_size1000, nums_sample) #標本抽出:サンプルサイズ1000、サンプル数1
print(sample10)
#標本平均、標本分散の計算
mean_s10, mean_var10 = sample10.mean(), sample10.var() #標本平均、標本分散
mean_s100, mean_var100 = sample100.mean(), sample100.var() #標本平均、標本分散
mean_s1000, mean_var1000 = sample1000.mean(), sample1000.var() #標本平均、標本分散
#中心極限定理を仮定
calc_std10 = std/np.sqrt(sample_size10) #標本平均の分布の標準偏差
calc_std100 = std/np.sqrt(sample_size100) #標本平均の分布の標準偏差
calc_std1000 = std/np.sqrt(sample_size1000) #標本平均の分布の標準偏差
print(f'標本数:{sample_size10} 平均:{mean_s10:.2f}, 分散:{mean_var10:.2f}, 標準誤差:{calc_std10:.2f}')
print(f'標本数:{sample_size100} 平均:{mean_s100:.2f}, 分散:{mean_var100:.2f}, 標準誤差:{calc_std100:.2f}')
print(f'標本数:{sample_size1000} 平均:{mean_s1000:.2f}, 分散:{mean_var1000:.2f}, 標準誤差:{calc_std1000:.2f}')
[OUT]
[[168.29 166.24 170.74 175.46 182.08 174.64 170.09 168.71 177.45 180.39]]
標本数:10 平均:172.30, 分散:17.47, 標準誤差:1.93
標本数:100 平均:172.17, 分散:27.20, 標準誤差:0.61
標本数:1000 平均:171.93, 分散:37.11, 標準誤差:0.19また中心極限定理における、各標本数nでの「標本平均の分布:平均=母平均、分散=標準誤差」をプロットしました。標本数が増えるほど標本平均のばらつきが小さくなり値が発生する区間(確率)が狭くなることが確認できます。
[IN]
#z値(標準化)
x = np.arange(145, 205, 1)
y10 = stats.norm.pdf(x, loc=mean, scale=calc_std10) #母平均μ、分散(標準誤差)σ^2/n
y100 = stats.norm.pdf(x, loc=mean, scale=calc_std100) #母平均μ、分散(標準誤差)σ^2/n
y1000 = stats.norm.pdf(x, loc=mean, scale=calc_std1000) #母平均μ、分散(標準誤差)σ^2/n
#可視化
fig, axs = plt.subplots(1, 3, figsize=(14, 6), facecolor='w')
axs = axs.ravel()
#標本平均をプロット
axs[0].scatter(mean_s10, 0, color='red', marker='*', s=100, label=f'標本平均')
axs[1].scatter(mean_s100, 0, color='red', marker='*', s=100, label=f'標本平均')
axs[2].scatter(mean_s1000, 0, color='red', marker='*', s=100, label=f'標本平均')
#標本平均の分布をプロット
make_plot(axs[0], x, y10, f'標本平均分布', f'標本数{sample_size10}の標本平均の分布')
make_plot(axs[1], x, y100, f'標本平均分布', f'標本数{sample_size100}の標本平均の分布')
make_plot(axs[2], x, y1000, f'標本平均分布', f'標本数{sample_size1000}の標本平均の分布')
plt.tight_layout()
plt.show()
[OUT]
5-3.標本平均の標準化:z値と標準正規分布
繰り返しですが中心極限定理より「標本数nが大きくなれば標本平均の分布の平均値は母平均$${\mu}$$、分散は$${\frac{\sigma^2}{n}}$$の正規分布」に近づきます。つまり「母分散が既知の場合、母平均$${\mu}$$を仮定すれば標本数nの標本平均$${\bar{x}}$$は標準化(標本平均の分布を標準化)」できます。推定では”求めたい真値”を母平均$${\mu}$$としてz値を計算します。
$$
標本平均を標準化=\frac{標本平均-母平均}{標本平均の分布の標準偏差}=\frac{\bar{x}-\mu}{\sqrt{\frac{\sigma^2}{n}}}
$$
$$
-1.96≦\frac{\bar x – μ}{\sqrt{\frac {σ^2}{n}}}≦1.96 (95%の信頼水準)
$$
$$
\bar{x} –1.96 \sqrt{\frac {σ^2}{n}} \le μ \le \bar{x} + 1.96\sqrt{\frac {σ^2}{n}}
$$

大まかな考え方のまとめは下図の通りです。

[IN]
#標準正規分布(平均0、分散1)
x = np.linspace(-4, 4, 100)
y_pdf = stats.norm.pdf(x, loc=0, scale=1)
#z値(標準化)
z10 = (mean_s10 - mean)/calc_std10
z100 = (mean_s100 - mean)/calc_std100
z1000 = (mean_s1000 - mean)/calc_std1000
print(f'z値 n={sample_size10}:{z10:.2f}, n={sample_size100}:{z100:.2f}, n={sample_size1000}:{z1000:.2f}')
fig = plt.figure(figsize=(8, 6), facecolor='w')
plt.plot(x, y_pdf, label='標準正規分布')
plt.scatter(z10, 0 , color='red', marker='o', s=50, alpha=0.5, label=f'n={sample_size10}, z値:{z10:.2f}')
plt.scatter(z100, 0 , color='green', marker='^', s=50, alpha=0.5, label=f'n={sample_size100}, z値:{z100:.2f}')
plt.scatter(z1000, 0 , color='blue', marker='*', s=50, alpha=0.5, label=f'n={sample_size1000}, z値:{z1000:.2f}')
plt.vlines(z10, 0, stats.norm.pdf(z10, loc=0, scale=1), color='red', linestyle='dashed')
plt.vlines(z100, 0, stats.norm.pdf(z100, loc=0, scale=1), color='green', linestyle='dashed')
plt.vlines(z1000, 0, stats.norm.pdf(z1000, loc=0, scale=1), color='blue', linestyle='dashed')
#信頼区間を記載
plt.fill_between(x, y_pdf, where=(x < 1.96) & (x > -1.96), color='red', alpha=0.2, label='95%信頼区間')
plt.fill_between(x, y_pdf, where=(x < 2.58) & (x > -2.58), color='orange', alpha=0.2, label='99%信頼区間')
plt.text(1.96, 0.1, 'σ=1.96', fontsize=12, color='red')
plt.text(-2.96, 0.1, '-σ=1.96', fontsize=12, color='red')
plt.text(2.58, 0.05, 'σ=2.58', fontsize=12, color='orange')
plt.text(-3.58, 0.05, '-σ=2.58', fontsize=12, color='orange')
plt.annotate('', xy=(1.96, 0.06), xytext=(1.96, 0.1), arrowprops=dict(arrowstyle='->', color='red'))
plt.annotate('', xy=(-1.96, 0.06), xytext=(-1.96, 0.1), arrowprops=dict(arrowstyle='->', color='red'))
plt.annotate('', xy=(2.58, 0.02), xytext=(2.58, 0.05), arrowprops=dict(arrowstyle='->', color='orange'))
plt.annotate('', xy=(-2.58, 0.02), xytext=(-2.58, 0.05), arrowprops=dict(arrowstyle='->', color='orange'))
plt.legend(loc='upper right'), plt.grid()
plt.show()
[OUT]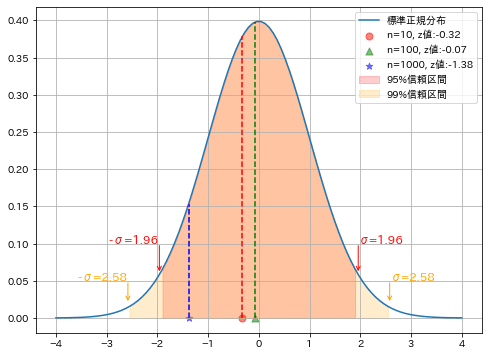
結果より下記が確認できました。
z値の計算では既知の母分散から計算した標準誤差を用いて、標本平均$${\bar{x}}$$求めたい母平均$${\mu}$$で標準化したものである。
「標本数nが大きいー>標準誤差が小さいー>z値が大きくなる」 ため、($${\bar{x}-\mu}$$)が小さくないとz値が大きくなり棄却される。つまり標本数nが大きいほど標本平均が真値に近づかないといけないため信頼性が高くなる。
標本数が一番大きいn=1000のz値が最も大きくなった。それでも信頼区間95%(標準正規分布の確率95%内)に入っているため、高確率で真値(仮定した母平均)であると判断できる。
本推定の流れは「標本抽出->母数の分散は既知と仮定->確率密度関数を正規分布と仮定して求めたい母平均で標本平均を標準化(z値)->標本平均の分布が正規分布ならz値が入るであろう区間を確認」となります。推定・検定はどこ(分布、平均、分散)を仮定するかは異なりますが基本的な考え方は同じとなります。
6.推定の実践
推定では「標本->母集団の統計量を推定」します。推定時には「母集団や標本平均の統計量や分布を仮定」して計算するため、各推定方法での前提は何かを理解しておく必要があります。
【仮定の例※詳細は各推定でご確認ください】
●母集団分布が特定の確率分布(正規分布など)に従う
●標本数nが十分にある。つまり中心極限定理より、標本平均の分布は分散$${\frac{\sigma^2}{n}}$$の正規分布に従う。
●統計量を使用するための条件が必要なものに関しては値を設定する(例:母集団の分散を既知 など)。
6-1.母平均の推定(母分散既知):正規分布
標本から母集団の平均値を推定します。本推定の前提は下記の通りです。
母集団の分布は正規分布に従う
母集団の分散は既知とする(※前提として計算するが通常は知りえない)
統計量としてはz値を使用する
$$
-1.96≦\frac{\bar x – μ}{\sqrt{\frac {σ^2}{n}}}≦1.96 (95%信頼区間)
$$
$$
\bar{x} –1.96 \sqrt{\frac {σ^2}{n}} \le μ \le \bar{x} + 1.96\sqrt{\frac {σ^2}{n}}
$$

参考例として工場での例(お菓子の袋詰めなど)を考えます。製品量が多いとコストUPになり少ないとクレームが出るため適切な条件で製造したいと考えております。
条件は下記であり、現在の製造が目標通り製造できているか確認します。
目標平均重量(母平均):300g
抽出数(サンプリングサイズ):20個
標本平均:306.3g
標準偏差:10g (※通常では知りえない値ですが知っているものと仮定)

[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
from scipy import stats
#母集団の作成
std_p = 10 #(母集団の)標準偏差σ
mean_s, nums_s = 306.3, 20 #標本の平均値、標本数
#統計量z値
def calc_Zvalue(mean_s, nums_s, std_p, C=0.95):
Confidence_Intervals = stats.norm.interval(C, loc=0, scale=1) #標準正規分布の信頼区間(累積分布関数)
z_lower, z_upper = Confidence_Intervals #信頼区間の下限、上限※下限は負の値
error_std = std_p / np.sqrt(nums_s) #標準誤差
#母平均の信頼区間
mean_p_lower = mean_s + z_lower * error_std #母平均の下限
mean_p_upper = mean_s + z_upper * error_std #母平均の上限
return (mean_p_lower, mean_p_upper)
result_95 = calc_Zvalue(mean_s, nums_s, std_p, C=0.95)
result_99 = calc_Zvalue(mean_s, nums_s, std_p, C=0.99)
print(f'95%信頼区間:{result_95[0]:.1f}~{result_95[1]:.1f}')
print(f'99%信頼区間:{result_99[0]:.1f}~{result_99[1]:.1f}')
[OUT]
95%信頼区間:301.9~310.7
99%信頼区間:300.5~312.1結果として下記が確認でき、結論としては「目標値より過剰に充填している(信頼区間から外れている)」と判断できます。
95%信頼区間・99%信頼区間ともに300gを外れている。つまり今回の標本の母平均が目標値である確率は低い。
95%より99%信頼区間の方が幅が広いのは「99%の確率で信頼区間が母平均を含む確率」のため、より安全サイド(幅が広がる)に変化するため
信頼区間の値は 「誤り:母平均は301.9~310.7gに95%の確率で存在」ではなく「正:301.9~310.7gの信頼区間を持つ標本を100個とったら95個は母平均に入る」ため、実際の母平均の値は不明である。
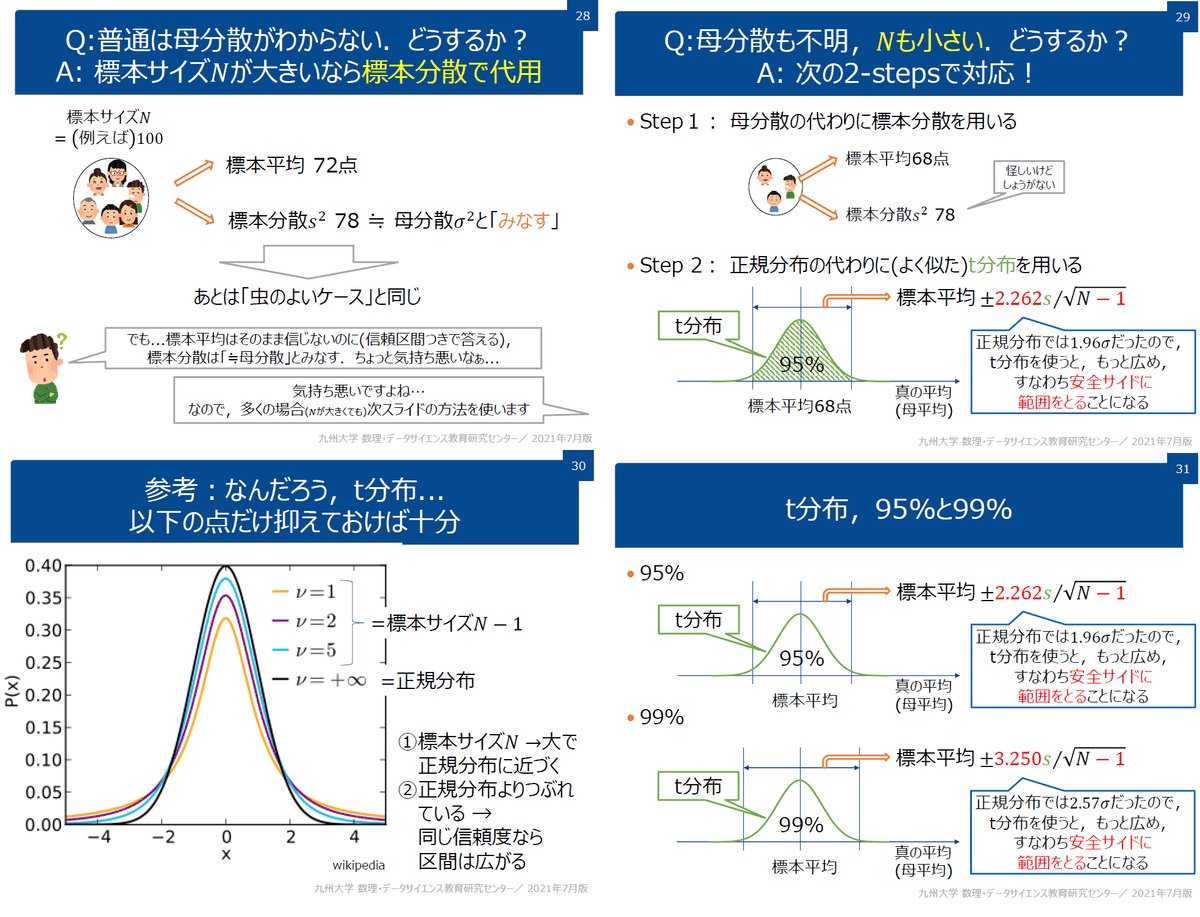
6-2.母平均の推定(母分散未知):t分布
前節では「母分散を既知」としましたが通常ではそのような値は知りえません。そこで標本の分散を使用して母集団の平均を求めます。
本推定の前提は下記の通りです。
母集団の分散は未知のため、標本の不偏分散で代用する
計算時には「自由度=サンプルサイズ-1」を使用する
不偏分散を用いて標準化と同じ計算をするため、準標準化と呼ばれる
不偏分散を使用するため、母集団の分布は正規分布ではなくt分布に従う。標本平均を準標準化した統計量Tはt分布に従う
分散既知の場合は信頼区間は正規分布で計算したが、本推定ではt分布に従い計算する
$$
t値(X%下限)≦\frac{\bar x – μ}{\frac {標本の不偏標準偏差σ}{\sqrt{n}}}≦t値((X%上限))
$$
$$
\bar{x} –t値_{下限}\sqrt{\frac {σ^2}{n}} \le μ \le \bar{x} + t値_{上限}\sqrt{\frac {σ^2}{n}}
$$
条件は前項とほぼ同等であり、現在の製造が目標通り製造できているか確認します(標本は分布が変わるため何パターンか作成しました)。
目標平均重量(母平均):300g
抽出数(サンプリングサイズ):2~20個
標本平均:306.3g
標本の不偏標準偏差:10g (※前述は母集団の標準偏差は既知ですが、今回は未知のため標本から不偏分散を計算したものとします)
[IN]
pd.options.display.float_format = '{:.2f}'.format #小数点以下2桁表示
#標本の統計量
mean_s = 306.3 #標本の平均値
nums_s = np.array([2,3,4,5,6,11,15,20]) #標本の標本数
d_free = nums_s - 1 #自由度
#標本の不偏標準偏差
std_s = 10.0
error_std = std_s / np.sqrt(nums_s) #標準誤差
_t_low = stats.t.ppf(0.025, d_free) #t分布の下側2.5%点
t_low = abs(_t_low) #t分布の上側2.5%点(絶対値)
mean_low = mean_s - t_low * error_std #母平均の下限
mean_high = mean_s + t_low * error_std #母平均の上限
df = pd.DataFrame({'標本数': nums_s,
'自由度': d_free,
'標準誤差': error_std,
'2.5%点t': t_low,
't分布の下側2.5%点': mean_low,
't分布の上側2.5%点': mean_high,
'分布の幅': mean_high - mean_low})
df
[OUT]
結果として下記が確認でき、結論としては「標本数n=15であれば、目標値より過剰に充填している(信頼区間から外れている)」と判断できます。
標本数(自由度)を増やすと推定区間が狭くなり推定の精度が高くなる
t分布を作成すると標本数を増やすとt分布がシャープ(平均値の高さが高くなり分散が小さくなる)ことが確認できます。
標本数が小さければ「目標値が母平均である確率」は増えるが分布の幅が大きすぎるため信頼性が下がる(サンプルサイズの設定が重要)
[IN]
x = np.arange(mean_s-3*std_s, mean_s+3*std_s, 0.01)
y = stats.norm.pdf(x, loc=mean_s, scale=std_s) #正規分布
y1 = stats.t.pdf(x, df=d_free[0], loc=mean_s, scale=std_s) #t分布
y2 = stats.t.pdf(x, df=d_free[1], loc=mean_s, scale=std_s) #t分布
y3 = stats.t.pdf(x, df=d_free[2], loc=mean_s, scale=std_s) #t分布
y4 = stats.t.pdf(x, df=d_free[3], loc=mean_s, scale=std_s) #t分布
y5 = stats.t.pdf(x, df=d_free[4], loc=mean_s, scale=std_s) #t分布
y6 = stats.t.pdf(x, df=d_free[5], loc=mean_s, scale=std_s) #t分布
y7 = stats.t.pdf(x, df=d_free[6], loc=mean_s, scale=std_s) #t分布
y8 = stats.t.pdf(x, df=d_free[7], loc=mean_s, scale=std_s) #t分布
fig, ax = plt.subplots(1, 1, figsize=(12, 6), facecolor='w')
ys = [y, y1, y2, y3, y4, y5, y6, y7, y8]
for idx, y in enumerate(ys):
if idx == 0:
ax.plot(x, y, label='正規分布', ls='--', color='black')
ax.plot(x, y, label=f't分布(自由度={idx})')
idx += 1
ax.set(title='t分布', xlabel='x', ylabel='確率密度関数')
plt.legend(), plt.grid()
plt.show()
[OUT]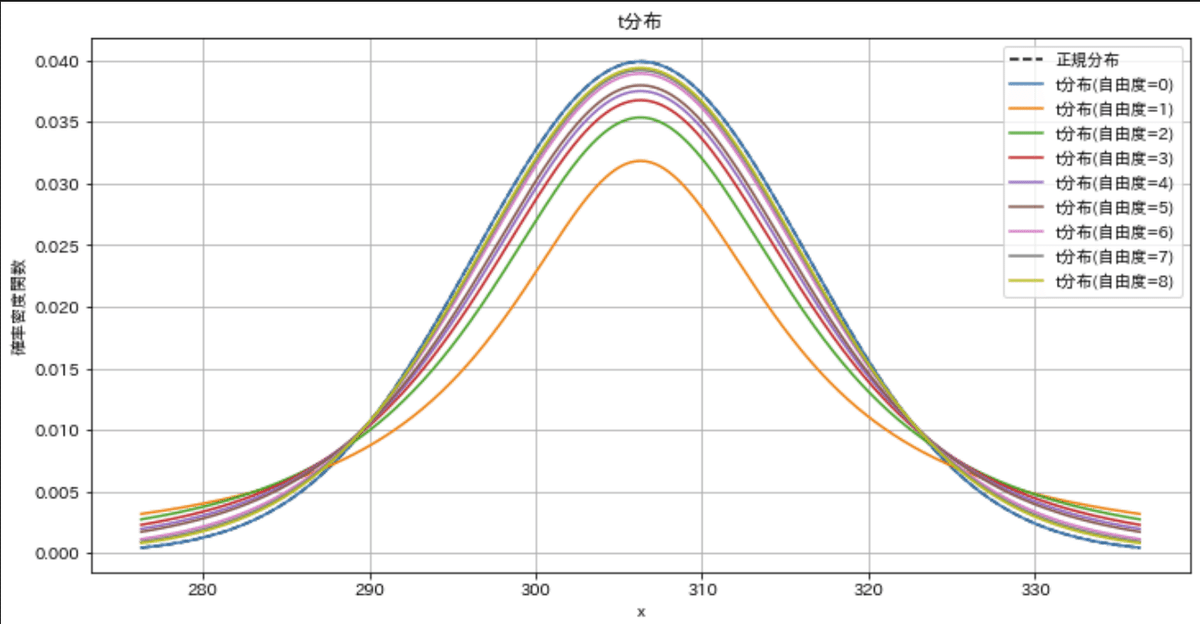
下記は参考図となります。
6-3.母平均の推定(母集団分布未知)
本推定では標本から母集団の平均値を推定します。本推定の前提は下記の通りです。
母集団の分布は不明である(母分散も不明)。
標本数nを大きく抽出する。中心極限定理より、標本平均は正規分布に従うとする。
標本を正規分布と仮定するため標本のデータを使用するが、不偏分散ではなく標本分散を使用する。
n:標本数、$${\bar x}$$:標本平均、σ:標本の標準偏差
$$
-1.96≦\frac{\bar x – μ}{\sqrt{\frac {σ^2}{n}}}≦1.96 (95%信頼区間)
$$
$$
\bar{x} –1.96 \sqrt{\frac {σ^2}{n}} \le μ \le \bar{x} + 1.96\sqrt{\frac {σ^2}{n}}
$$
例として下記のような条件であれば前項と同じ形で計算できます。標本数の"たくさん"は一部主観が入るためt分布などと合わせて分析が必要となります。
目標平均重量(母平均):300g
抽出数(サンプリングサイズ):たくさん(中心極限定理が成り立つ)
標本平均:306.3g
標本分散の標準偏差(標本から計算):10g
[IN]
-
[OUT]
-6-4.母比率の推定:ベルヌーイ分布
標本(標本の比率p)から母集団の母比率を推定します。本推定の前提は下記の通りです。
母集団の分布は不明である(母分散も不明)。
標本数nを大きく抽出する。中心極限定理より、標本平均は正規分布に従うとする。
母集団はベルヌーイ分布に従う。
標本数:R、母比率:p、母分散p(1-p)、標本の比率:R
$$
-1.96≦\frac{R – p}{\sqrt{\frac {p(1-p)}{n}}}≦1.96 (95%信頼区間)
$$
nが十分におおきいときは大数の法則よりRはpに近づくため下記となる。
$$
-1.96≦\frac{R – p}{\sqrt{\frac {R(1-R)}{n}}}≦1.96 (95%信頼区間)
$$
参考例として工場での不良品発生率を考えます。条件は下記であり、現在の製造が目標通り製造できているか確認します。
標本数(製品の抜き取り数):100個
標本内の不良品数:10個
標本の不良品比率:0.1 ($${\frac{10}{100}}$$)

下記の通り実際の発生率(母比率)は標本より高い可能性もあるため、目標値がもっと低い場合は①サンプリングを多くして精度をあげる、②そもそもの不良品を下げる 必要があります
[IN]
nums = 100 #標本数(抜き取りサンプル数)
nums_defective = 10 #不良品数
R = nums_defective / nums #不良率(標本確率)
error_std = np.sqrt(R * (1 - R) / nums) #標準誤差
ci = 0.95 #信頼係数
z_min, z_upper = stats.norm.interval(ci, loc=0, scale=1) #信頼区間
p_low = R + z_min * error_std #不良率の下限
p_high = R + z_upper * error_std #不良率の上限
print(f'不良率の下限: {p_low:.4f}, 不良率の上限: {p_high:.4f}')
[OUT]
不良率の下限: 0.0412, 不良率の上限: 0.15886-5.母分散の推定:カイ二乗分布
標本(標本の標準偏差σ)から母集団の分散を推定します。本推定の前提は下記の通りです。
母集団の分布は正規分布(母分散は不明であり求めたい値)。
$${χ^2}$$分布に従う
他の分布と異なり左右非対称の分布となる
参考例として工場での製品のばらつきを考えます。条件は下記であり、現在の製造のばらつきの真値を確認します。
標本数(製品の抜き取り数):100個 (※計算は自由度を使用)
標本の標準偏差:10 (標本分散から算出)
[IN]
nums = np.array([100]) #標本数(抜き取りサンプル数)
ds_free = nums - 1 #自由度
std_s = np.array([10]) #標本標準偏差
ci = np.array([0.95]) #信頼係数
t_low, t_high = stats.chi2.interval(ci, df=ds_free) #カイ二乗分布の信頼区間
var_low = (ds_free * std_s**2) / t_high #分散の下限
var_high = (ds_free * std_s**2) / t_low #分散の上限
std_low, std_high = np.sqrt(var_low), np.sqrt(var_high) #標準偏差の下限、上限
df = pd.DataFrame({'標本数': nums,
'自由度': ds_free,
'下側2.5%点': t_low,
'上側2.5%点': t_high,
'分散_下部限界値': var_low,
'分散_上部限界値': var_high,
'σ_下部限界値': std_low,
'σ_上部限界値': std_high
})
df.T
[OUT]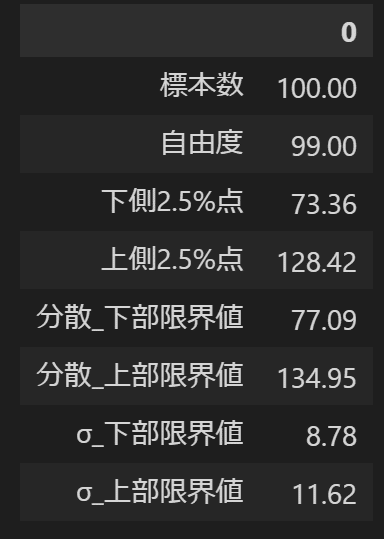
参考資料
Python
データ用
https://dashboard.e-stat.go.jp/
あとがき
追って追記予定
