
Pythonライブラリ(多次元配列):Numpy
概要
Numpyは配列操作や線形代数の処理ができるライブラリです。機械学習ライブラリのPytorchを学びたい方はAPIが似ているため学んで損はないです。
なお線形代数np.linalgは数式の説明が多くなるため別記事にしました。
1.Numpyの基本操作1
1-1.numpy配列:np.array()
numpy配列の作成はnp.array()の引数にリスト形式で入力します。リストを多次元にするとベクトル・行列・テンソルの作成が可能です。
[In]
import numpy as np
array1 = np.array(1)
array2 = np.array([1, 2, 3]) #np.array(list(range(1,4)))と同じ
array3 = np.array([1, 2, 3], dtype=np.float32) #floatに変換
array4 = np.array([[1, 2], [3, 4], [5, 6]])[Out] ※print文省略
array(1)
array([1, 2, 3])
array([1., 2., 3.], dtype=float32)
array([[1, 2],
[3, 4],
[5, 6]])1-2.配列情報の取得:shape, dtype, ndim, size
配列情報の取得は下記の通りです。
●shape:(多次元)配列の形状
●dtype:配列内のデータ型
●ndim:配列の次元数
●size:配列全体のパラメータ数
[In]
print(f'配列形状:{array1.shape, array2.shape, array3.shape, array4.shape}')
print(f'データの型:{array1.dtype, array2.dtype, array3.dtype, array4.dtype}')
print(f'次元数:{array1.ndim, array2.ndim, array3.ndim, array3.ndim}')
print(f'要素数(パラメータ数):{array1.size, array2.size, array3.size, array4.size}')[Out]
配列形状:((), (3,), (3,), (3, 2))
データの型:(dtype('int32'), dtype('int32'), dtype('float32'), dtype('int32'))
次元数:(0, 1, 1, 1)
要素数(パラメータ数):(1, 3, 3, 6)1-3.データ型の変換:array.astype(型)
データ型を変更する場合はastype()メソッドを使用します。
[In]
array = np.array(1)
array_f = np.array(1).astype('f') #floatに変換
array_f, array_f.dtype
[Out]
array(1., dtype=float32), dtype('float32')1-4.出力値の小数点表示形式:np.set_printoptions()
numpyで出力される値の表示値の確認:np.get_printoptions()、設定:np.set_printoptions()となります。
[In]
np.get_printoptions() # 数値の表示設定
np.set_printoptions(precision=3) #小数点3桁に変更
[Out]
{'edgeitems': 3, 'threshold': 1000, 'floatmode': 'maxprec', 'precision': 8,
'suppress': False, 'linewidth': 75, 'nanstr': 'nan', 'infstr': 'inf',
'sign': '-', 'formatter': None, 'legacy': False}[In]デフォルト設定/Reset
np.set_printoptions(edgeitems=3, infstr='inf',
linewidth=75, nanstr='nan', precision=8,
suppress=False, threshold=1000, formatter=None)2.Numpyの基本操作2:データ抽出/ソート
2-1.データ抽出1:スライス
データの抽出・スライスをします。リスト操作とほぼ同じです
[In]
import numpy as np
array = np.array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23]])
array
array[0] # 1行目を抽出
array[:2] # 2行目までを抽出
array[:, 3:] # 3列目以降を抽出
array[0, 1] # 1行2列目を抽出
array[1][1] # 1行1列目を抽出※上と同じ
array[0:2, 3:5] # 1-2行、3-4列目を抽出[Out]下記はイメージ図
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23]])
array([0, 1, 2, 3, 4, 5])
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11]])
array([[ 3, 4, 5],
[ 9, 10, 11],
[15, 16, 17],
[21, 22, 23]])
1
7
array([[ 3, 4],
[ 9, 10]])

2-2.データ抽出2:整数配列
numpy配列を部分抽出する場合は下記のような整数配列を使用します。
[In]
array[[1,2,3], [1,3,2]]
# np.array([array[1,1], array[2,3], array[3,2]]) #同上
[Out]
array([ 7, 15, 20])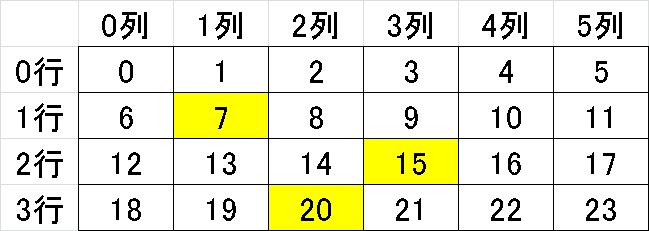
2-3.数値のソート:np.sort()
数値をソートする場合はnp.sort()を使用します。
[In]1次元配列
a_1dim = np.array([69, 87, 3, 12, 45])
a_sort = np.sort(a_1dim) #配列を昇順にソート
a_sortinv = np.sort(a_1dim)[::-1] #配列を降順にソート
[Out]
array([ 3, 12, 45, 69, 87])
array([87, 69, 45, 12, 3])多次元配列の場合は1次元より複雑になります。
[In]多次元配列
a_2dim = np.array([[ 60, 0, 70, 30, 50, 10],
[100, 80, 20, 40, 90, 110]])
a_sort = np.sort(a_2dim) #配列を昇順にソート
a_sortax0 = np.sort(a_2dim, axis=0) #行方向に昇順にソート
a_sortinv = np.sort(a_2dim)[::-1] #配列を降順にソート
a_sort1dim = np.sort(a_2dim, axis=None) #1次元配列に変換
a_sortall = np.sort(a_2dim, axis=None).reshape(a_2dim.shape) #1次元配列でソート後にreshapeで形状復元[Out]
array([[ 0, 10, 30, 50, 60, 70],
[ 20, 40, 80, 90, 100, 110]])
array([[ 60, 0, 20, 30, 50, 10],
[100, 80, 70, 40, 90, 110]])
array([[ 20, 40, 80, 90, 100, 110],
[ 0, 10, 30, 50, 60, 70]])
array([ 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110])
array([[ 0, 10, 20, 30, 40, 50],
[ 60, 70, 80, 90, 100, 110]])2-4.ソートのインデックス番号取得: np.argsort()
ソート順のインデックス番号を返すのがnp.argsort()です。また戻り値のインデックス番号を使用して値を抽出することもできます。
[In]1次元配列
a_1dim = np.array([69, 87, 3, 12, 45])
a_sort = np.argsort(a_1dim) #配列を昇順にソート
a_sortinv = np.argsort(a_1dim)[::-1] #配列を降順にソート
a_sval = a_1dim[a_sort]
a_svalinv = a_1dim[a_sortinv]
display(a_sort, a_sortinv, a_sval, a_svalinv)[Out]
array([2, 3, 4, 0, 1], dtype=int64)
array([1, 0, 4, 3, 2], dtype=int64)
array([ 3, 12, 45, 69, 87])
array([87, 69, 45, 12, 3])多次元配列の場合は値抽出は各行で処理が必要です。
[In]
a_2dim = np.array([[ 60, 0, 70, 30, 50, 10],
[100, 80, 20, 40, 90, 110]])
a_argsort_h = np.argsort(a_2dim) #axis=1、横方向にソート順のインデックスを返す
a_argsort_v = np.argsort(a_2dim, axis=0) #縦方向にソート順のインデックスを返す
a_vals = a_2dim.ravel()[np.argsort(a_2dim.ravel())].reshape(a_2dim.shape)[Out]
array([[1, 5, 3, 4, 0, 2],
[2, 3, 1, 4, 0, 5]], dtype=int64)
array([[0, 0, 1, 0, 0, 0],
[1, 1, 0, 1, 1, 1]], dtype=int64)
array([[ 0, 10, 20, 30, 40, 50],
[ 60, 70, 80, 90, 100, 110]])3.連続値配列・標準行列
3-1.連続値配列の作成:np.arange(), np.linspace()
連続値の配列は下記で作成できます。
●np.arange():整数での連数を作成
●np.linspace(開始値、終値、データ数):データ数-1で分割した連数
[In]
array1 = np.arange(10) #開始値:0, 終了値x-1, ステップ:1
array2 = np.arange(3, 10) #開始値:3, 終了値x-1, ステップ:1
array3 = np.arange(0, 10, 2) #開始値:0, 終了値x-1, ステップ:2
[Out] ※print文省略
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
array([3, 4, 5, 6, 7, 8, 9])
array([0, 2, 4, 6, 8])[In]
ary_lin1 = np.linspace(0, 1) #0~1を49個に分割(データ数は50)
ary_lin2 = np.linspace(0, 1, 11) #0~1を10個に分割(データ数は11)
print('ary_lin1形状:', ary_lin1.shape, 'ary_lin2形状:', ary_lin2.shape)
[Out] ※print文省略
array([0. , 0.02040816, 0.04081633, 0.06122449, 0.08163265,
0.10204082, 0.12244898, 0.14285714, 0.16326531, 0.18367347,
0.20408163, 0.2244898 , 0.24489796, 0.26530612, 0.28571429,
0.30612245, 0.32653061, 0.34693878, 0.36734694, 0.3877551 ,
0.40816327, 0.42857143, 0.44897959, 0.46938776, 0.48979592,
0.51020408, 0.53061224, 0.55102041, 0.57142857, 0.59183673,
0.6122449 , 0.63265306, 0.65306122, 0.67346939, 0.69387755,
0.71428571, 0.73469388, 0.75510204, 0.7755102 , 0.79591837,
0.81632653, 0.83673469, 0.85714286, 0.87755102, 0.89795918,
0.91836735, 0.93877551, 0.95918367, 0.97959184, 1. ])
array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ])
ary_lin1形状: (50,) ary_lin2形状: (11,)3-2.標準行列:np.zeros, np.ones, np.full, np.eye
特定の形・数値の配列を作成する場合は下記のメソッドがあります。
●np.zeros(ゼロ行列):すべての値が0の行列を作成
●np.ones(1行列):すべての値が1の行列を作成
●np.full(行列指定):指定した形状・値の行列を作成
●np.eye(単位行列):対角成分のみ 1でそれ以外は 0である正方行列
[In] #ゼロ行列
np_zero1 = np.zeros(3) #形状(3,)の0行列(ベクトル)
np_zero2 = np.zeros([2, 2]) #np.zeros([行数a×列数b])でa×bのゼロ行列
_np = np.array([[1, 2, 3], [4, 5, 6]]) #参考配列:形状(2,3)
np_zero3 = np.zeros_like(_np) #_npと同形状のゼロ行列
[Out] ※print文省略
array([0., 0., 0.])
array([[0., 0.],
[0., 0.]])
array([[0, 0, 0],
[0, 0, 0]])[In] #1行列
np_one1 = np.ones(3) #形状(3,)の1行列
np_one2 = np.ones([2, 2]) #np.ones([行数a×列数b])でa×bの1行列となる。
_np = np.array([[1, 2, 3], [4, 5, 6]]) #参考配列:形状(2,3)
np_one3 = np.ones_like(_np) #_npと同形状の1行列
[Out]
array([1., 1., 1.])
array([[1., 1.],
[1., 1.]])
array([[1, 1, 1],
[1, 1, 1]])[In] #行列を指定
np_full1 = np.full(3,1) #1次元配列:値が1の(3,)行列
np_full2 = np.full([2,3],1) #多次元配列:値が1の多次元配列
np_full3 = np.full([2,3], np.nan) #空行列も作成可能
[Out]
array([1, 1, 1])
array([[1, 1, 1],
[1, 1, 1]])
array([[nan, nan, nan],
[nan, nan, nan]])[In]
np_eye1 = np.eye(2) #np.eye(次元数n)でn×nの単位行列となる。
np_eye2 = np.eye(3, 6) #出力参照
[Out]
array([[1., 0.],
[0., 1.]])
array([[1., 0., 0., 0., 0., 0.],
[0., 1., 0., 0., 0., 0.],
[0., 0., 1., 0., 0., 0.]])3-3.格子列の生成:np.meshgrid()
指定の配列の値に対して格子状のグリッドを作成します。x=[x1, x2, x3], y=[y1, y2]の配列の場合における出力およびポイントは下記の通りです。
X:columns、Y:indexとして配置した値が各行列に沿って埋まる
出力は渡した引数と同じ数が出力(X, Yの2つなら2個生成)
得られた出力を四則演算することでX, Yの各値を全パターン抽出可能
[IN]
class HorizontalDisplay:
def __init__(self, *args):
self.args = args
def _repr_html_(self):
template = '<div style="float: left; padding: 10px;">{0}</div>'
return "\n".join(template.format(arg._repr_html_())
for arg in self.args)
import pandas as pd
idx = [f'y{i+4}' for i in range(2)] #output: ['y4', 'y5']
cols = [f'x{i+1}' for i in range(3)] #output: ['x1', 'x2', 'x3']
df = pd.DataFrame(np.full([2,3], ''), index=idx, columns=cols) #2×3の空のDataFrameを作成
Xs = np.array([cols]*2).reshape(2,3)
Ys = np.array([idx[0]]*3+[idx[1]]*3).reshape(2,3)
df_X = pd.DataFrame(Xs, index=idx, columns=cols)
df_Y = pd.DataFrame(Ys, index=idx, columns=cols)
HorizontalDisplay(df, df_X, df_Y, df_X+'+'+df_Y)
[OUT]
Numpyを使用したコードは下記の通りでありポイントは①出力はリスト型であり数は引数と同じ、②出力値の各行列サイズは(y, x)となる。
[IN]
x = np.array([1,2,3])
y = np.array([4,5])
print(x.shape, y.shape)
x_grid = np.meshgrid(x, y)
print(type(x_grid), len(x_grid), x_grid[0].shape, x_grid[1].shape)
print(x_grid)
print(x_grid[0]+x_grid[1])
[OUT]
(3,) (2,)
<class 'list'> 2 (2, 3) (2, 3)
[array([[1, 2, 3],
[1, 2, 3]]),
array([[4, 4, 4],
[5, 5, 5]])]
array([[5, 6, 7],
[6, 7, 8]])これの良い点は「各配列から1個ずつデータを選択した時の全組合せを抽出できる」です。例として配列xの数3、配列yの数2の場合全パターンは6つあり、Meshで作成した配列を使用することで各パターンを全抽出可能です。
[IN]
x = np.array([1,2,3])
y = np.array([10,20])
X, Y = np.meshgrid(x, y)
print(X + Y)
pd.DataFrame((X + Y), index=[f'y={i}' for i in y], columns=[f'x={i}' for i in x])
[OUT]
array([[11, 12, 13],
[21, 22, 23]])
4.形状操作(配列変換)
4-1.配列形状の変換:array.reshape()
配列の形状の変換はnp.reshape()を使用します。
[In]
array = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) # array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
array_re1 = array.reshape(2, 5) #(行数, 列数)へ変換
array_re2= array.reshape(2, -1) #-1を選択すると、片方の数値を指定して残り(-1)の方は自動で計算する。[Out] #array_re1, array_re2は同出力
array([[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]]) 4-2.配列の1次元化:array.ravel()
配列を1次元化するにはarray.ravel()を使用します。
[In]
array_ravel = array_re2.ravel() #配列を一次元に変換
[Out]
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])4-3.配列の転置:np.transpose()/array.T
配列の転置(次元数を入れ替える)はarray.Tを使用します。多次元配列において次元を指定する場合はtransposeメソッド()を使用します。
[In]
array = np.array([[ 0, 1, 2],
[ 6, 7, 8]]) #配列形状: (2, 6)
array.T
np.transpose(array) #array.Tと同じ
[Out] ※array.Tとnp.transpose(array)の出力
array([[0, 6],
[1, 7],
[2, 8]])[In]
array_3dim = np.array([[[0, 1, 2],
[3, 4, 5]],
[[6, 7, 8],
[9, 10, 11]]]) #形状(2, 2, 3)の3次元配列
array_3dim.T #array_3dim.transpose(2,1,0)と同じ 形状(3, 2, 2)
array_3dim.transpose(0,2,1) #形状(2, 3, 2)の3次元配
[Out]
array([[[ 0, 6],
[ 3, 9]],
[[ 1, 7],
[ 4, 10]],
[[ 2, 8],
[ 5, 11]]])
array([[[ 0, 3],
[ 1, 4],
[ 2, 5]],
[[ 6, 9],
[ 7, 10],
[ 8, 11]]])4-4.次元の追加:np.newaxis
新しい次元を追加する場合はnp.newaxisを使用します。配列が持つ数値は変更されず挿入された次元サイズは1になります。
[In]
array = np.array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11]]) #配列形状: (2, 6)
array1_ = array[np.newaxis] #(1, 2, 6)
array2 = array[np.newaxis, :, :] #(1, 2, 6)
array3 = array[:, np.newaxis, :] #(2, 1, 6)
array4 = array[:, :, np.newaxis] #(2, 6, 1)
print('配列形状:', array.shape, array1_.shape, array2.shape, array3.shape, array4.shape)
[Out]
配列形状: (2, 6) (1, 2, 6) (1, 2, 6) (2, 1, 6) (2, 6, 1)4-5.配列の拡張:np.expand_dims(axis)
配列の拡張(np.newaxisのように次元を追加したり、reshapeのように配列を変更)する場合は"np.expand_dims"メソッドを使用します。
[IN]
import numpy as np
x = np.array([1, 2]) #Original: shap=(2,)
print(f'x: {x}', x.shape)
#1次元配列を2次元配列に変換
y1 = np.expand_dims(x, axis=0) #x[np.newaxis, :] or x[np.newaxis]と同じ
print(f'y1: {y1}, shape:{y1.shape}')
#1次元配列に変更
y2 = np.expand_dims(x, axis=1) #x[:, np.newaxis]と同
print(f'y2: {y2}, shape:{y2.shape}')
#Tupleでの指定も可能
_y1 = np.expand_dims(x, axis=(0, 1)) #
_y2 = np.expand_dims(x, axis=(2, 0)) #
print(f'_y1: {_y1}, shape:{_y1.shape}')
print(f'_y2: {_y2}, shape:{_y2.shape}')[OUT]
x: [1 2] (2,)
y1: [[1 2]], shape:(1, 2)
y2: [[1]
[2]], shape:(2, 1)
_y1: [[[1 2]]], shape:(1, 1, 2)
_y2: [[[1]
[2]]], shape:(1, 2, 1)5.条件抽出
5-1.シンプルな条件抽出
シンプルな手法としてnumpy配列に比較演算子を加えるとBool型配列を取得できます。それを元の配列に入れると指定値を抽出できます。
[In]
array = np.array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11]])
a_bool = array > 7 #7超の数値はTrue, 以下はFalse
a_up7 = array[array > 7] #7超の数値のみ抽出
[Out]
array([[False, False, False, False, False, False],
[False, False, True, True, True, True]])
array([ 8, 9, 10, 11])5-2.条件抽出+置換:np.where()
指定した条件のTrue/Falseに対して値を置換する場合はnp.where(条件, Trueの値, Falseの値)を使用します。
[In]
array = np.array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11]])
np.where(array > 7, 0, 1) #np.where(条件、置き換える値、条件を満たさない要素の値)
[Out]
array([[1, 1, 1, 1, 1, 1],
[1, 1, 0, 0, 0, 0]])5-3.下限/上限(min/max)を設定:np.clip()
配列の下限・上限設定はnp.clip(配列、下限値、上限値)を使用します。
[In]
array = np.array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11]])
np.clip(array,2,7) #np.clip(data, min, max)としてmin以下の数値はすべてmin, max以上の数値はすべてmaxにする。
[Out]
array([[2, 2, 2, 3, 4, 5],
[6, 7, 7, 7, 7, 7]])6.統計量取得
統計情報および指定値のインデックス番号を取得します。
合計:sum, 平均:mean, 分散:var, 標準偏差:std, 最大:max, 最小:min
最大値index:argmax, 最小値index:argmin
6-1.全般(sum, mean, std)
一般的な統計量は"np.xx()"または"array.xx()"で取得可能です。。
[In]'1次元配列'
a = np.array([1,2,3,5,7,9,10,11])
print('sum:', np.sum(a), 'avg:', np.mean(a),'var:', np.var(a), 'std:', np.std(a) ) #合計・平均・分散・標準偏差
print('max:', np.max(a), 'min:', np.min(a)) #最大値, 最小値
[Out]
sum: 48 avg: 6.0 var: 12.75 std: 3.570714214271425
max: 11 min: 1[In]'2次元配列'
a_2D = [[ 1, 2, 3, 5],
[ 7, 9, 10, 11]]
print('sum:', np.sum(a_2D), 'avg:', np.mean(a_2D),'var:', np.var(a_2D), 'std:', np.std(a_2D) ) #合計・平均・分散・標準偏差
print('max:', np.max(a_2D), 'min:', np.min(a_2D)) #最大値, 最小値
[Out]
sum: 48 avg: 6.0 var: 12.75 std: 3.570714214271425
max: 11 min: 16-2.nan値を除外した統計値:nansum(), nanmean()
配列にnan(None)が入っている場合そのまま統計値を取得しようとするとエラーが出ます。nanを無視した統計量は下記の通りです。
【nanを無視した統計値】
●合計:np.nansum()
●平均:np.nanmena()
[IN]
array = np.array([1, np.nan, 2, 3])
print(f'array.sum():{array.sum()}')
print(f'np.nansum(array):{np.nansum(array)}')
[OUT]
array.sum():nan
np.nansum(array):6.0[IN]
np.nanmean(array)
[OUT]
2.06-3.最大/最小値のindex取得:argmax/argmin
配列内の最大値/最小値があるindex番号取得は”argmax(),argmin()”を使用します。機械学習では分類においてone-hotベクトル内で最も高い(高い架空率をもつ)indexの抽出などに使用されます。
[IN]
a = np.array([1,2,3,5,7,9,10,11])
print('argmax:', np.argmax(a),'argmin:', np.argmin(a)) #最大値のindex番号, 最小値のindex番号
[OUT]
argmax: 7 argmin: 0[IN]
a_2D = [[ 1, 2, 3, 5],
[ 7, 9, 10, 11]]
print('argmax:', np.argmax(a_2D),'argmin:', np.argmin(a_2D)) #最大値のindex番号, 最小値のindex番号
print(np.argmax(a_2D, axis=0), np.argmax(a_2D, axis=1)) #最大値のindex番号を軸方向で取得->axis=0で列方向、axis=1で行方向
[OUT]
argmax: 7 argmin: 0
[1 1 1 1] [3 3]6-4.統計分布(パーセンタイル):np.percentile
パーセンタイルとは数値を小さい順から並べた時にその数値が何%に該当するかを示す指標であり外れ値の確認に使用できます。。
なお25, 50, 75%は四分位数と呼ばれており「25パーセンタイル(第一四分位数)」、「50パーセンタイル(中央値)」、「75パーセンタイル(第三四分位数)」となります。
Numpyではパーセンタイルは”np.percentile(<array>, <何%値か>)”で計算できます。サンプルでは外れ値を設けることで特定のパーセンタイル以上で数値が急激に上昇することが確認できました。
[IN]
import numpy as np
A = np.array([0, 1, 2, 3, 4, 5, 6, 90, 100])
print([100*i/(len(A)-1) for i in range(len(A))])
print(f'25%percentile:{np.percentile(A, 25)}')
print(f'50%percentile:{np.percentile(A, 50)}')
print(f'75%percentile:{np.percentile(A, 75)}')
print(f'85%percentile:{np.percentile(A, 85)}')
print(f'95%percentile:{np.percentile(A, 95)}')
[OUT]
[0.0, 12.5, 25.0, 37.5, 50.0, 62.5, 75.0, 87.5, 100.0]
25%percentile:2.0
50%percentile:4.0
75%percentile:6.0
85%percentile:73.19999999999999
95%percentile:96.07.ランダム操作
7-1.データのシャッフル:random.shuffle()
配列のランダムな並び替えはnp.random.shuffle(array)を使用します。
[In]
array = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
np.random.shuffle(array) #配列をランダムに並び替える
array
[Out]
array([5, 7, 2, 4, 1, 0, 3, 6, 8, 9])7-2.データのランダム抽出:random.choice()
NumpyのArrayやイテラブル内の値から指定した数をランダムに抽出する場合は"np.random.choice(<array>)"を使用します。
【引数一覧】
●a(1-D array-like or int):値を抽出するためのarray, イテラブル
●size(int or tuple of ints, optional){default:False}:抽出するデータサイズ
->(m, n, k)ならm * n * kのサンプルを抽出(Noneだと1つの値(スカラー)出力)
●replace(boolean, optional){default:True}:重複して抽出するか(Falseの場合同じ値は使用されずデータ数以上だとエラーが発生)
●p(1-D array-like, optional):指定なしならaからランダムに抽出
[IN]
array = np.array([0, 1, 2, 3, 4])
print(np.random.choice(array, 3))
print(np.random.choice(array, (2,3)))
[OUT]
[1 0 3]
[[1 4 1]
[2 0 4]][IN]
print(np.random.choice(array, 5))
print(np.random.choice(array, 5, replace=False))
print(np.random.choice(array, 10))
print(np.random.choice(array, 10, replace=False))
[OUT]
[0 0 4 4 2]
[0 3 2 1 4]
[0 0 4 4 2 4 1 2 4 1]
ValueError: Cannot take a larger sample than population when 'replace=False'7-3.乱数作成
7-3-1.乱数の基礎知識:疑似乱数(線形合同法)
乱数は文字通りランダムな値ですがPCは命令したことしかできないため理想上のランダムは実現できません。PCは疑似乱数を使用しており、基本的な乱数生成方法は下記の線形合同法となります。
$$
x_{i+1} = a x_i + b \mathrm{~mod~} m \quad (a \ge 1, b \ge 0 ,m \ge 2 \mathrm{:~定数}, x:seed) \\
メルセンヌ-ツイスターではM=2^{19937}-1を使用するため乱数周期が長く高次元に均一に分布する
$$
http://www.math.sci.hiroshima-u.ac.jp/m-mat/TEACH/ichimura-sho-koen.pdf
参考として手動で乱数を作成しました。Numpyでの「np.random.rand」と同様の挙動を示すことが確認できました。
[IN]
import matplotlib.pyplot as plt
import numpy as np
#線形合同法:乱数生成器
class RandGenerator:
def __init__(self, seed):
self.A = 48271
self.B = 1
self.M = 2**31 - 1 #メルセンヌ・ツイスターでは2**19937-1を使用
self.seed = seed
def __call__(self):
s_next = (self.A*self.seed + self.B) % self.M
self.seed = s_next
return s_next/self.M
seed = 0
rand_gen = RandGenerator(seed)
nums_random = [rand_gen() for i in range(10000)]
plt.hist(nums_random, bins=20)
[OUT]
(array([500., 532., 465., 503., 507., 500., 529., 521., 529., 497., 516.,
449., 467., 525., 491., 505., 496., 499., 493., 476.]),
array([4.65661288e-10, 4.99999930e-02, 9.99999855e-02, 1.49999978e-01,
1.99999971e-01, 2.49999963e-01, 2.99999956e-01, 3.49999948e-01,
3.99999941e-01, 4.49999933e-01, 4.99999926e-01, 5.49999918e-01,
5.99999911e-01, 6.49999903e-01, 6.99999896e-01, 7.49999888e-01,
7.99999881e-01, 8.49999873e-01, 8.99999866e-01, 9.49999858e-01,
9.99999851e-01]),
<BarContainer object of 20 artists>)
7-3-2.乱数の実装:np.random
np.random()で乱数値を作成します。

●np.random.rand(データ数(データ形状)):0~1の間でランダムに生成
●np.random.randn(データ数(データ形状)):標準正規分布(平均0, 分散1)
●np.random.randint(最小値, 最大値, データ数):整数値のランダム
●np.random.permutation(順列数):順列(0から入力値を1刻み)のランダム
●np.random.binomial(試行回数, 確率, サンプル数):二項分類 ※紹介のみ
random()では多次元配列を作成できますが、下記サンプルは比較しやすいように1次元配列で作成しました。
[In]
np.random.seed(0)
random_rand = np.random.rand(10000) #0~1の間でランダムに生成
random_n = np.random.randn(10000) #標準正規分布(平均0, 分散1)の乱数
random_int = np.random.randint(0, 100, 10000) #(最小値, 最大値, データ数)で整数値をランダムで作成
random_permutation = np.random.permutation(10000) #0~指定された数値までの整数値をランダムで取得
#以下はNumpy関係なし**************************************
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
import japanize_matplotlib
japanize_matplotlib.japanize()
plt.rcParams["font.size"] = 16
fig = plt.figure(figsize=(20,18))
figrow, figcol = 2, 2 #fig.add_subplotの行列を指定
axelist = [] #fig.add_subplotで作成したaxeを保管しておくリスト->編集時に呼び出す
y_datas = [random_rand, random_n, random_int, random_permutation] #プロットしたいデータリスト:ここでは3種
y_datas_str = []
for var in globals():
if 'random' in var:y_datas_str.append(var)
for idx, data in enumerate(zip(y_datas, y_datas_str)):
data, name = data
axelist.append(fig.add_subplot(figrow, figcol, idx+1)) #リストの中に指定したaxeを追加
n, bins, patches = axelist[idx].hist(data, 100, color='dodgerblue') #リストから呼び出したaxeにデータをプロット
axelist[idx].plot([data.mean(),data.mean()], [0,n.max()], label='平均値', c='red', linewidth=1)
axelist[idx].plot([data.std(),data.std()], [0,n.max()], label='標準偏差σ', c='pink', linewidth=1, linestyle='dashed')
data_std = data.mean() + (data.mean()-data.std())
axelist[idx].plot([data_std,data_std], [0,n.max()], label='標準偏差σ', c='pink', linewidth=1, linestyle='dashed')
axelist[idx].set_title(f'{name}, 平均値:{round(data.mean(),2)}, 標準偏差:{round(data.std(),2)}')
plt.legend()
plt.show()
8.配列の結合:np.concatenate, xstack
配列を結合する場合は np.vstack・np.hstackまたはnp.concatenateを使用します(多分どっちも同じ)。
[In]
array1 = np.array([[1, 2, 3],
[4, 5, 6]])
array2 = np.array([[10, 11, 12],
[13, 14, 15]])
#vertical(垂直)方向に結合
array_v = np.vstack([array1, array2])
np.concatenate([array1, array2], axis=0) #axis=0でvertical方向に結合
#Horizontal(水平)方向に結合
array_h = np.hstack([array1, array2])
np.concatenate([array1, array2], axis=1) #axis=1でhorizontal方向に結合
display(array_v, array_h)[Out] np.stackとnp.concatenateは同じ出力
array([[ 1, 2, 3],
[ 4, 5, 6],
[10, 11, 12],
[13, 14, 15]])
array([[ 1, 2, 3, 10, 11, 12],
[ 4, 5, 6, 13, 14, 15]])9.配列の計算
9-1.四則演算・その他基礎演算
各種演算・留意事項は下記の通りです。
●和差商積:numpy配列同士に+, -, *, / で計算可能
●累乗:array**nまたはnp.power(array, 乗数)
●平方根(ルート):np.sqrt(array)
●指数関数・対数関数:np.exp(array)、np.log1p(array)
9-2.アダマール積・内積
9-2-1.アダマール積
Numpyでアダマール積を計算する時は掛け算と同じ”*”を使用します。
[IN]
array1 = np.array([[1, 2],
[3, 4]])
array2 = np.array([[10, 20],
[30, 40]])
print(array1*array2) #アダマール積
[OUT]
[[ 10 40]
[ 90 160]]$$
\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ \end{bmatrix}\bigodot\begin{bmatrix} 10&20\\30&40\\\end{bmatrix}=\begin{bmatrix} 1×10&2×20\\3×30&4×40\\\end{bmatrix}=\begin{bmatrix} 10&40\\90&160\\\end{bmatrix}[1324]⨀[10302040]=[1×103×302×204×40]=[109040160]
$$
9-2-2.内積:np.matmul, np.dot(), @
Numpyで内積を計算する時は3種類の記法があります。コード内で統一しておけば好きな記法で問題ないと思います。
np.matmul(<arr1>, <arr2>):numpyのmatmulメソッドを使用
arr1@arr2:掛け算のように"@"を使用(matmul()と同じ動作)
np.dot(<arr1>, <arr2>):numpyのdotメソッドを使用※状況次第でアダマール積になる可能性がある
arr1.dot(<arr2>):配列のdotメソッドを使用
[IN]
np.matmul(array1, array2)
np.dot(array1, array2) #内積
array1@array2
array1.dot(array2)
[OUT]※3つもと同じ結果
array([[ 70, 100],
[150, 220]])$$
\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ \end{bmatrix}\begin{bmatrix} 10&20\\30&40\\\end{bmatrix}=\begin{bmatrix} 1×10+2×30&1×20+2×40\\3×10+4×30&3×20+4×40\\\end{bmatrix}=\begin{bmatrix} 70&100\\150&220\\\end{bmatrix}[1324][10302040]=[1×10+2×303×10+4×301×20+2×403×20+4×40]=[70150100220]
$$
9-3.原点からxy座標の距離(2乗和の√):np.hypot()
原点(x,y=0,0)からx, y座標距離はnp.hypot(<x>,<y>)を使用します。
[IN]
np.hypot(1,1)
[OUT]
1.4142135623730951参考例:sinθカーブをx,y座標で表示させると円から距離のためすべて半径(r=1.0)になります。
[IN]
theta = np.linspace(0, 1, 11)*2*np.pi
x = np.cos(theta)
y = np.sin(theta)
radius = np.hypot(x, y)
print(radius)
fig = plt.figure(figsize=(14,6))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
ax1.plot(theta, y, 'o', label='sinθ')
ax2.plot(x, y, 'o', label='sinθ')
[OUT]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
9-4.隣り合う要素の差分:np.diff()
配列の隣り合う要素通しの差分はnp.diff()で計算できます。
[IN]
import numpy as np
array = np.array([1, 2, 4, 7])
diff = np.diff(array) #隣り合う要素の差分を計算
diff
[OUT]
array([1, 2, 3])2次元配列の場合はaxisで行列方向を指定可能です。
[IN]
diff = np.diff(arr_2d) #Default:axis=1(列方向)
diff_row = np.diff(arr_2d, axis=0) #行方向に差分を計算
display(diff, diff_row)
[OUT]
array([[ 4, -1, -2],
[ 7, -6, 3],
[ 1, -2, 3]])
array([[ 1, 4, -1, 4],
[ 1, -5, -1, -1]])9-5.勾配の計算:np.gradient
配列同士の勾配はnp.gradient()で計算可能です。
[IN]
x = np.array([1,2,3], dtype=float)
y = np.array([1,2,4], dtype=float)
print(np.gradient(y, x)) #yの微分
[OUT]
[1. 1.5 2. ]9-6.畳み込み積分・移動平均:np.convolve
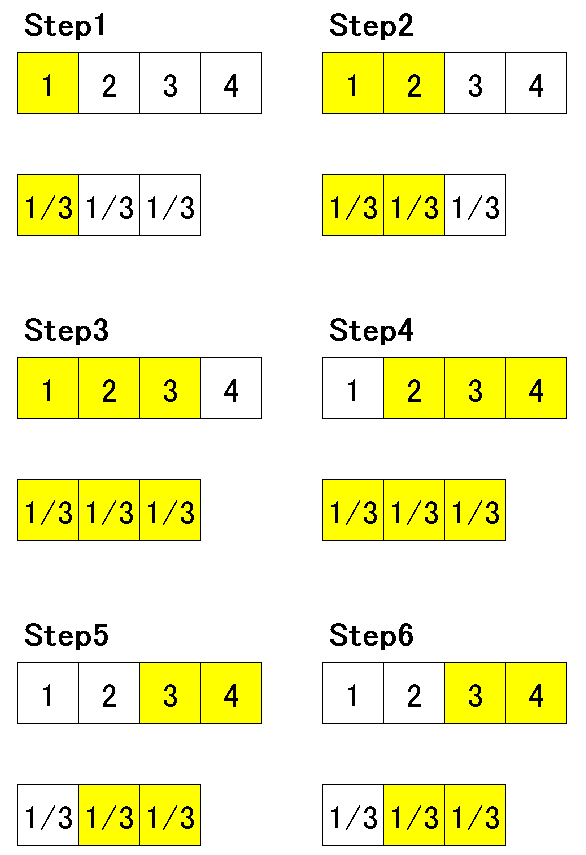
畳み込み積分をする場合はnp.convolve(<配列>, <フィルター>)を使用します。
下記の通りフィルターを分数倍にすると移動平均を作成することが出来ます。
[IN]
import numpy as np
a = [1,2,3,4]
v = [1/3,1/3,1/3]
np.convolve(a, v)
[OUT]
array([0.33333333, 1. , 2. , 3. , 2.33333333,
1.33333333])$$
output=(\frac{1}{3},\frac{1+2}{3} \frac{1+2+3}{3},\frac{2+3+4}{3} \frac{3+4}{3},\frac{5}{3})
$$
10.関数処理
Numpyでは1次元配列に関数を適用する場合は下記の通り簡単に実行できます。本章ではそれ以外のパターンに関して記載しました。
[IN]
import numpy as np
x = np.array([-2, -1, 0, 1, 2])
def multiply_x(x):
return x * 2
print(multiply_x(x))
[OOUT]
[-4 -2 0 2 4]10-1.多次元(配列)の関数処理:np.vectorize()
多次元の配列を一つの関数で処理する場合は"np.vectorize()"メソッドを使用します。
[IN]
x = np.array([-2, -1, 0, 1, 2])
y = np.array([2, -1, 0, -1, 2])
def classify_xy(x, y):
if x>0 and y>0:
return 'x:+, y:+'
elif x<0 and y<0:
return 'x:-, y:-'
elif x>0 and y<0:
return 'x:+, y:-'
elif x<0 and y>0:
return 'x:-, y:+'
elif x==0 and y==0:
return 'x:0, y:0'
else:
None
np.vectorize(classify_xy)(x, y)
[OUT]
array(['x:-, y:+', 'x:-, y:-', 'x:0, y:0', 'x:+, y:-', 'x:+, y:+'],
dtype='<U8')11.ブロードキャスト機能
ざっくりいうと配列形状の自動補完機能です。ルールとして「2つの配列の各次元が同じ大きさになっているか、どちらかが1であること」です。
例として下記のような計算ができます。
[In]
array = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
array*100 #スカラーである100が(3,3)形状の100の行列で計算される
[Out]
array([[100, 200, 300],
[400, 500, 600],
[700, 800, 900]]) 参考資料
NVIDIA GPUがあり環境構築済みであればNumpyと同じAPIでGPUを使用した演算が可能です。
あとがき
最近メインで使ってないので十分な内容がないかもしれないため、自分が困ったときに使用した内容をどんどん追記する予定です。
