
文系の blender 4.3 はじめての Geometry Nodes 基礎編 2 - Translate 動かす
ジオメトリノードのごく基礎、基本から学んでみます。第 2 回では、なにかを動かす、移動させるという操作をいくつかのパターンにわけて紹介します。
ジオメトリノードの解説やチュートリアルには英語の情報が多いため、ここでは言語を英語とし、日本語は可能なかぎり併記します。なお、ジオメトリノードの初歩的な作成方法等は、基礎編 1 - そもそもジオメトリノードとは を参照してください。
環境 Blender 4.3.0 , Mac Mini M1 OS 14.4
Object の移動
オブジェクトを移動させるには、Transform Geometry ノード内、Translationの値を変更する。
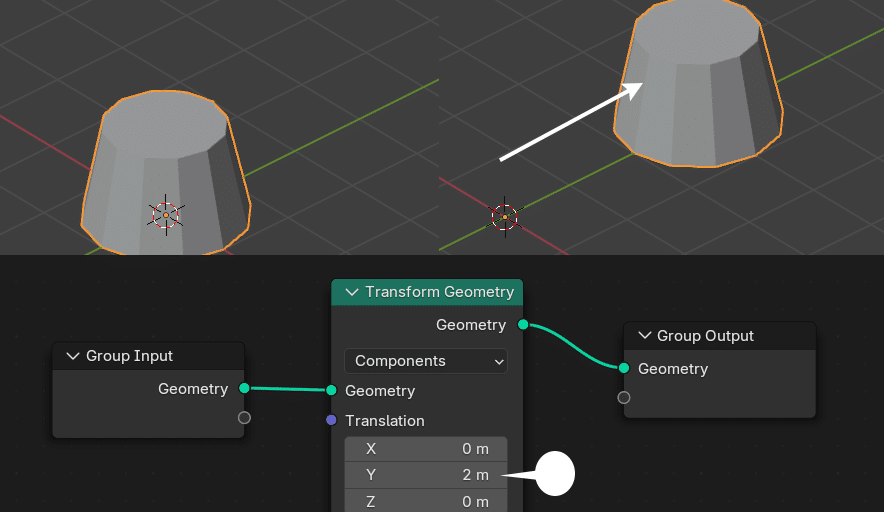
通常の操作では、G Y 2 キーを押したときと同じ。
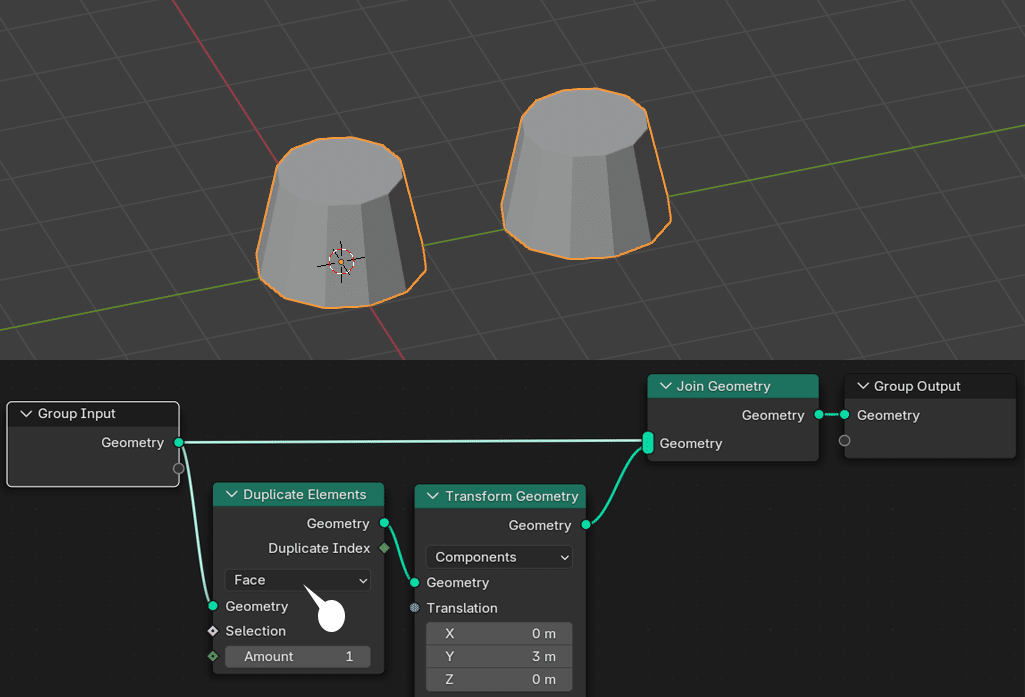
上では、オリジナルのオブジェクトを複製し、Y 軸に 3 m 移動、もとのオリジナルオブジェクトと統合している。Shift + D Y 3 キーと同じ。
Vertex の移動
オブジェクトの各頂点を移動させるには、Set Position ノードを使う。
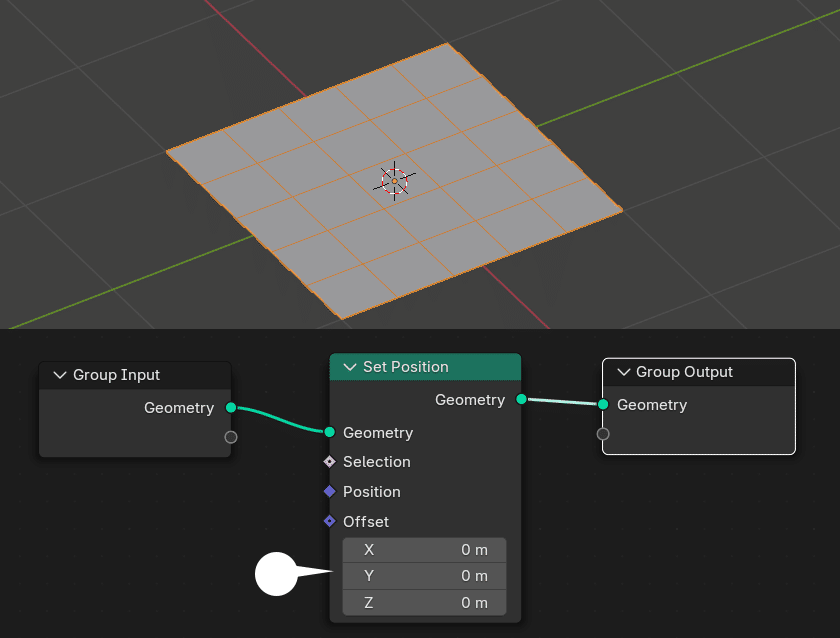
Offset
たとえば、上のようなやや細分化した平面オブジェクトの場合。Offset(オフセット)の各軸の値を変更すると、全体が移動して、上の Geometry Transform ノードと変わらない。これは、「すべての頂点」が同じ値で移動しているためだ。
そこで、Offset の値に、Random Value ノードによるランダムな「乱数」を与えてみる。


細かくなり文系には辛いところもあるが、Random Value から出力されるのは、1.26 , 0.78 , 1.51 , 0.25 … というような乱数の連続だ。
このため、各頂点の座標には、[x + 1.26 , y + 1.26 , z + 1.26] , [x + 0.78 , y + 0.78 , z + 0.78] … と、各座標に同じ値が加えられる。では、x, y, z 座標それぞれに異なったランダムな値を加えるには?

それには、Random Value のデータタイプを「Vector(ベクトル)」に変更する。


文系的には、とりあえず、Float とは、小数点以下を持つ数値で、Vector とは、[1.2 , 4.7 , 3.1 ]のように、3 つの値がセットになったデータと考えよう。Vector(ベクトル)は、データに [ x , y , z ]座標を持つことの多い 3DCG には欠かせないデータタイプだ。

また細かくなるが、データタイプを Vector に変更すると、Random Value ノードのソケットの色も変化(灰色(Float)から、青(Vector)へ)する。同時に、ソケット間の接続ラインのカラーも変わる。双方のソケットのデータタイプがどちらも同じ(青(Vector))になりました、という印だ。

なお、ひし形のソケットは、そのタイプが「Field(フィールド)」であり、丸いソケットのように単一の値ではなく、数列のような複数の値をやりとりできることを示している。ソケット間が点線になっているのは、フィールドデータが送られているという印だ。

Texture
なお、このような、フィールド値を送ることができるノードには、この他に、シェーダーエディターでもおなじみの、各種テクスチャがある。


上では、波テクスチャによって生成された数値のフィールド値を、Combine XYZ(XYZ合成)ノードを介して、各頂点の Offset の Z 軸(高さ)のみ変更させ、形状を変形させている。
Combine XYZ(XYZ合成) および、Separate XYZ(XYZ分離)ノードは、ベクトルデータと、数値(Float等)データの変換によく使うので覚えておこう。

左の Combine XYZ ノードは、数値のフィールド値を Z にのみ受けとり、[0 , 0, Z ]のベクトルのフィールド値として出力している。(Z が 8.2, 3.6 … ならば、出力は [0, 0, 8.2] , [0, 0, 3.6] … )
右では、ベクトルのフィールド値を受けとり、Z の値のみ数値のフィールド値として出力している。([3.7 , 5.5, 8.2 ] , [4.5 , 2.1 , 2.6 ]… ならば、8.2 , 2.6 … )
Position
上の Offset にように、現状の座標[ x , y , z ]にそれぞれ値を加える操作と異なり、Position(位置指定)は、座標[ x , y , z ]を直接指定するタイプだ。


ここでは、0.0 〜 1.0 までの乱数の ベクトルデータをそれぞれの頂点の座標に、既存の座標とは関係なく直接指定しているため、各頂点の位置が無作為なバラバラな状態になっているためだ。
そこで、ノードを下のように組んでみる。


ここで行っていることは、まず、Position ノードで各頂点の既存の座標データ(ベクトル)を出力、そこへ、前述の Random Value によるランダムなベクトルデータを加算(Add)している。Vector Math ノードは、ベクトルデータ同士の四則演算などができるノードだ。

Offset の操作のほうが、どちらかといえばわかりやすいかもしれないが、現状の座標に関係なく、各頂点を移動させ新たな形状を作りたい場合などは、Position の操作が適しているだろう。
まとめ
文系的にはすこしややこしい解説が続きましたが、外国語でいえば、文法の理解にあたるところなので、どうしても避けては通ることができません。最初はさっぱりなんだかよくわからない、という点が多いかもしれませんが、外国語の習得と同じで、さいしょは頭が痛くても、数をこなしていくうちに、だんだん慣れてきます。
基礎の積み重ねがあると、いつのまにか、これはあれでできるかも、と応用につながります。ひととおり試して、頭を慣らしてみてください。参考まで。
こんな文系なわたしですが、親族にはなぜか理系が多く、ベクトルってなんだかよくわからない、というと、それはこういうことですよ、と嬉しそうに説明してくれるのですが、なおもポカンとしていると、だんだん不思議な動物をみるような目で見られます。
