
文系の blender 4.3 はじめての Geometry Nodes 基礎編 3 - Rotate 回す
ジオメトリノードのごく基礎、基本から学んでみます。第 3 回では、なにかを回転させるという操作をいくつかのパターンにわけて紹介します。
環境 Blender 4.3.0 , Mac Mini M1 OS 14.4
ジオメトリノードの解説やチュートリアルには英語の情報が多いため、ここでは言語を英語とし、日本語は可能なかぎり併記します。なお、ジオメトリノードの初歩的な作成方法等は、基礎編 1 - そもそもジオメトリノードとは を参照してください。
オブジェクトの回転
オブジェクトを回転させるには、Transform Geometry ノード内、Rotation の値を変更する。
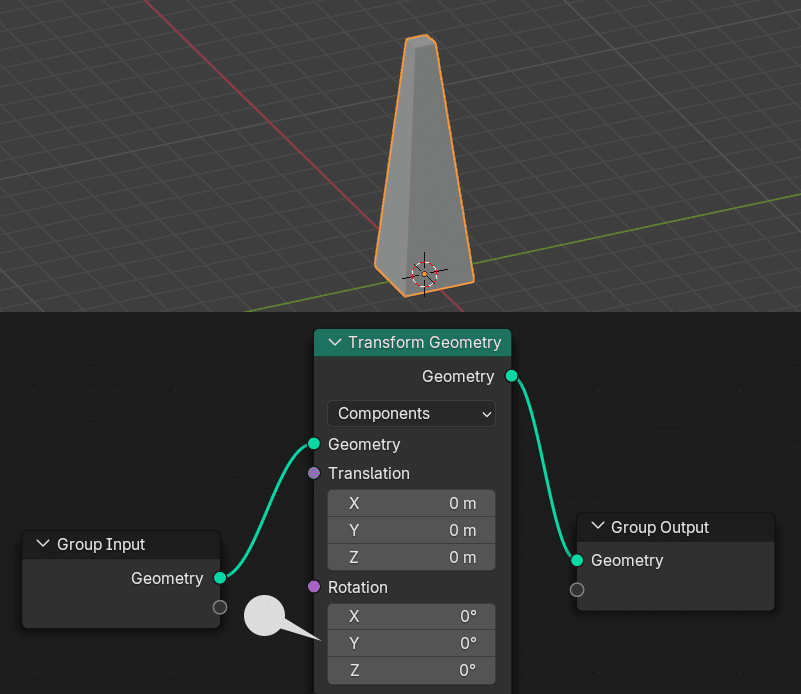


オブジェクトが、オブジェクト原点を基点に、それぞれの軸で回転する。通常の操作では、R X 90 や、 R Z -90 キー で行っていることと同じ。
文系的には細かくなるが、Transform Geometry ノードの Rotation の各値の単位は、われわれには馴染みのある、90° などの度(Angles, Degrees)だ。ただ、同時に、通常の数値(Float など)も与えることができる。
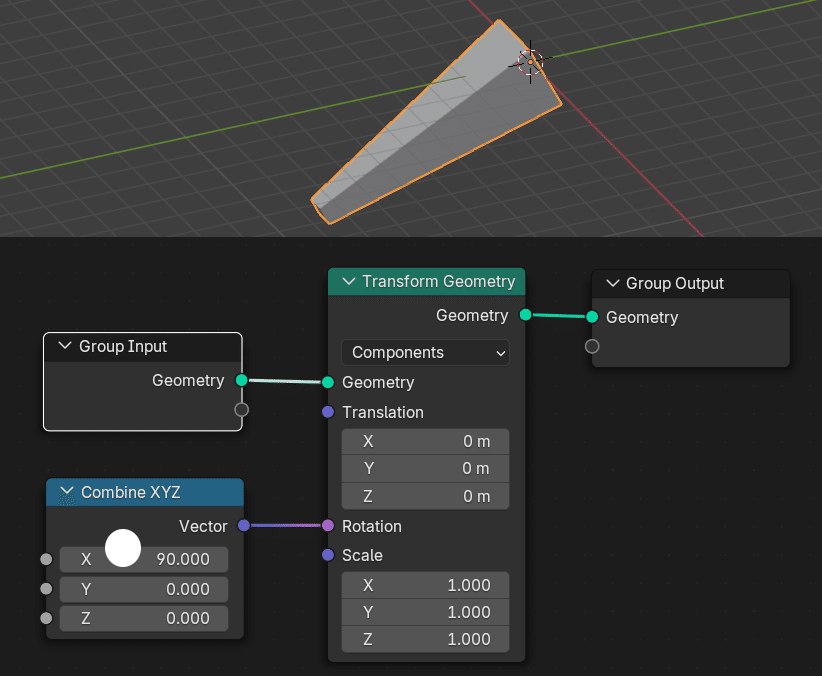
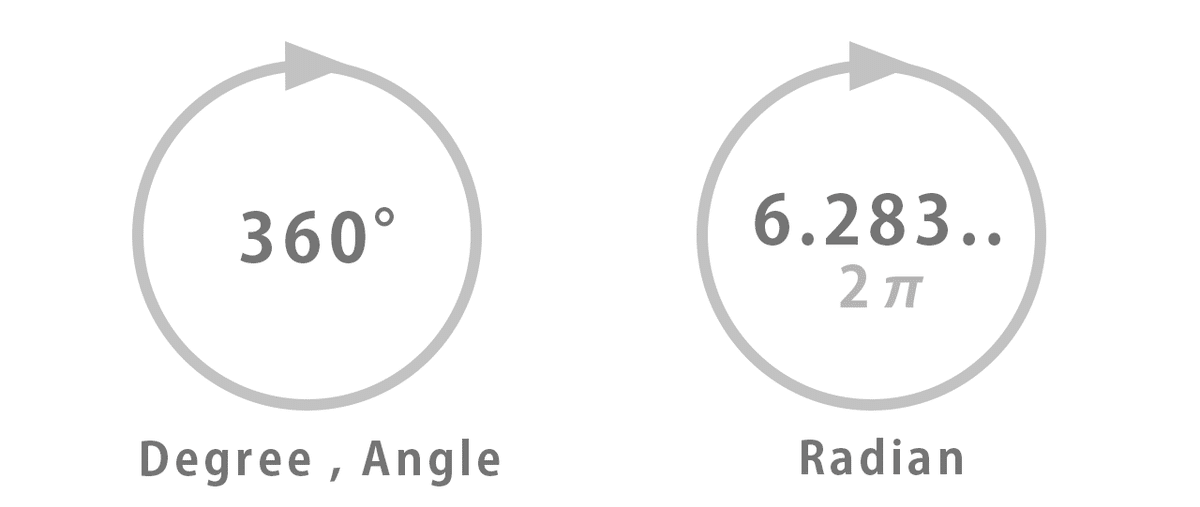
明らかに 90 度回転していない。通常の数値を回転値に与える場合、90 radians(ラジアン)という単位になるためだ。1度は、π÷180 radiansで、90度は、約 1.571 radians。変換するには、入力フィールドに radians(90) と入力する。(※逆は、degrees(1.571))

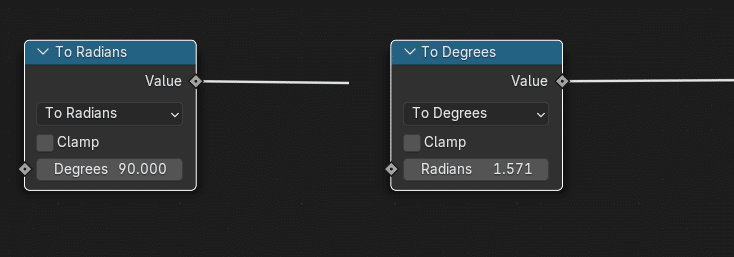
ちなみに、Math ノードで、双方の単位の値を変換することもできる。数値を回転値に与えなくてはならないこともあるので、おぼえておこう。
頂点の回転
オブジェクトそのものではなく、オブジェクトの各頂点を回転させるには?
細かくなるが、以降のジオメトリノードの操作は、頂点を回転させるというよりは、頂点に回転値を与えながら移動させる、という操作になる。
Set Position
オブジェクトの各頂点を回転させるには、Set Position ノードを使う。
細分化した辺オブジェクト(原点は底)に下のジオメトリノードを適用した。
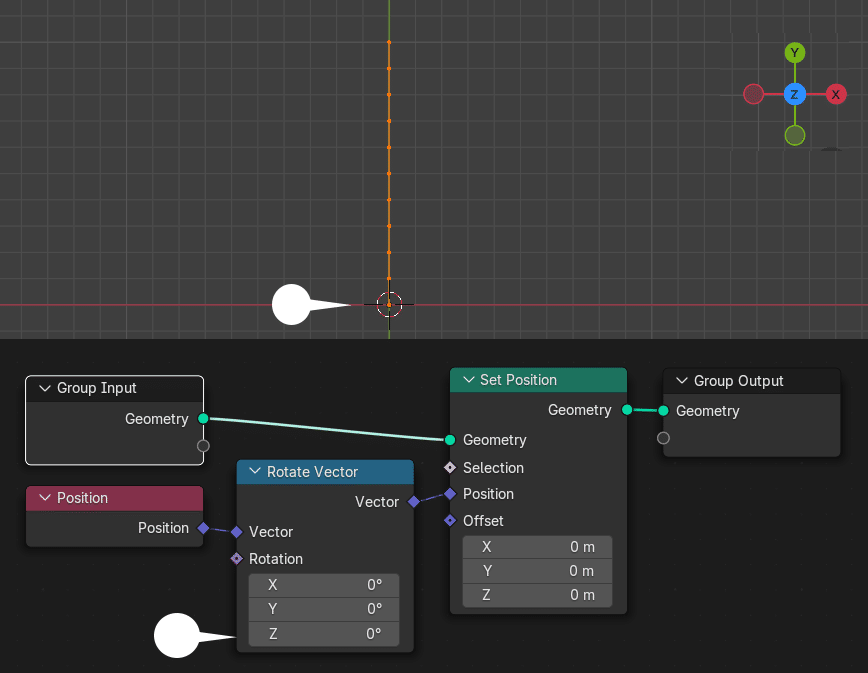
Position ノードから各頂点の現在の座標を出力し、そこへRotate Vectorで回転値を加え、Set Position ノードの各頂点の Position に適用する。
Rotate Vectorノードの Rotation > Z の値を 90°に変更。
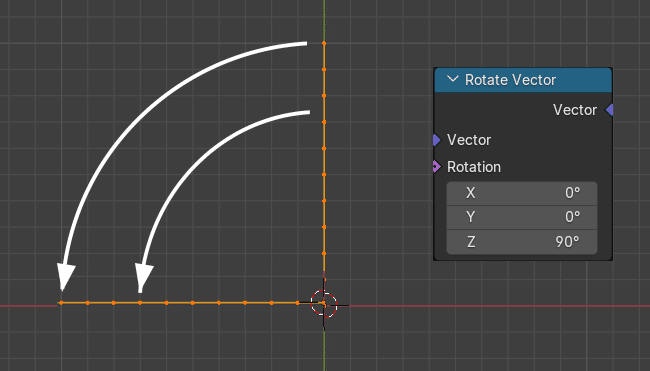
辺オブジェクトが原点を軸に90°回転する。それぞれの頂点が原点を軸を回転する点では、Transform Geometry ノードによるオブジェクトの回転と変わらない。
そこで、それぞれの頂点に異なる回転値を加えてみる。ノードを下のように変更した。

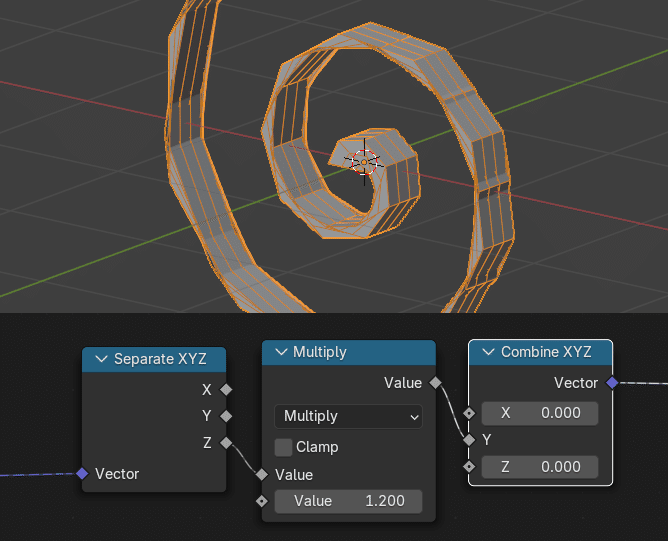
Position ノードから各頂点の現在の座標を出力、Separate XYZ で Y 値のみ抽出、 Combine XYZ ノードで、その値を Z 軸の回転値として Rotation ソケットに渡している。Multiply ノードは値の調整。
このため、Y 値が大きい(上では高い位置にある)頂点ほど、大きな回転値を与えられることになる。
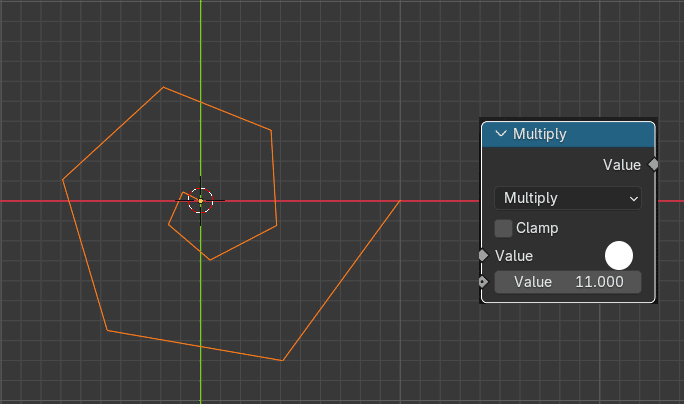
先端ほど回転値が大きくなり、渦状の形になった。
同ノードを細分化した平面オブジェクトに適用した。原点は中央。


同じノードを同様に細分化し、縦長の立方体オブジェクトに適用した。原点は底中央。
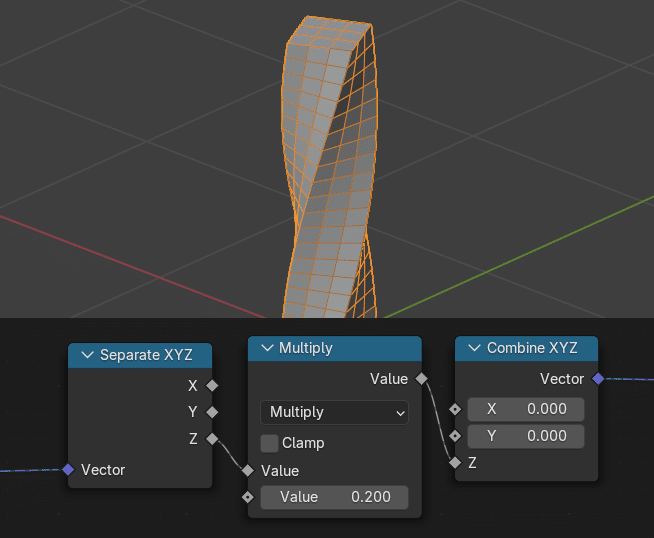
結果として、シンプル変形モディファイア とほぼ同じ操作を行っていることになる。
すこしおもしろい形状にはなるが、原点などの基点を軸に、回転値を与える、という点では、通常のオブジェクトモードや編集モードでの作業と変わらない。
ただ、なんらかの規則性や単純な数式をもとにさまざまなバリエーションを手軽に加えることができるのはやはりジオメトリノードの利点だ。
ベクトルと回転?
私の理解範囲内でまとめると、「ベクトル(Vector)」とは、少なくともジオメトリノード内では、3 つの値がセットになったデータであり、x, y, z の座標を与えれば位置を表すベクトルデータであり、x°, y°, x° など角度を与えれば、各軸の回転を表すベクトルデータだ。

細かくなるが、左の Vector ノードを Position (位置)ソケットに接続すれば位置を示し、Rotation(回転) ソケットに接続すれば、各軸 1.571 radian(約90°)の回転を示す。つまり、どちらのノードもほぼ同じ値を出力していて、分かりやすいように便宜的に別れているが、単位が異なるので扱いにくいものの、どちらも等しく、位置、回転データとして使うことはできる。
ベクトルは方向でもある
そのうえで、数学の教科書的な理解ではこちらのほうが一般的なのかもしれないが、同時に、ベクトルは向き、方向を表すデータでもある。
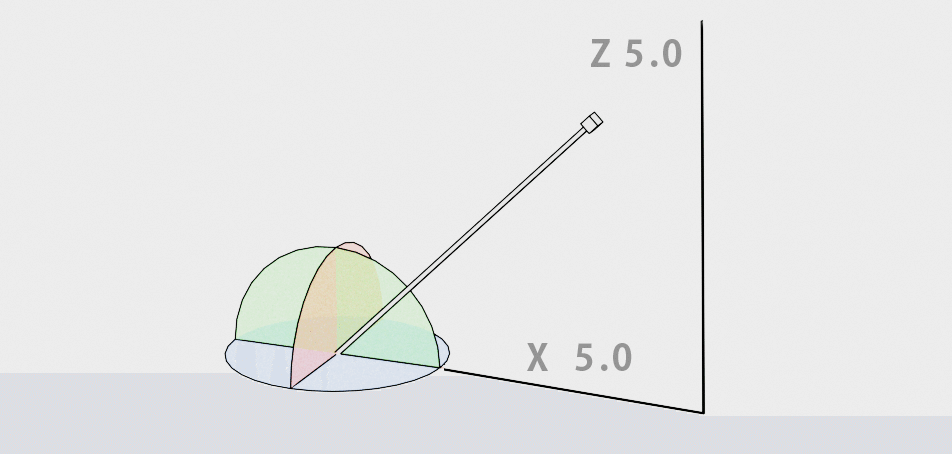
中央の棒状のオブジェクトに下のジオメトリノードを適用した場合。ベクトルを方向として扱うことのできる Align Rotation to Vector ノードに X 5.0 , Z 5.0 を与えた。

原点を軸に、位置 (5.0 , 0 , 5.0)を指すように棒オブジェクトが回転する。結果として、Y 軸に 45°回転させたのと同じ。あるオブジェクトの位置に応じて、別のオブジェクトをその方向に回転させる、というような操作に利用できる。
文系的には、ジオメトリノードでのベクトルとは、3 つの値がセットになったデータで、おもに位置、回転を表し、原点を軸とした「方向」も表すこともできる、という理解でよいのではないか。間違いはご指摘ください。
なお、素朴な疑問として、360度以上の値を与えてしまったらどうなるのだろうとわたしは心配してしまうが、時計の 25 時が午前 1 時になるように、380 度は 20 度になる。

消えたオイラー?
4.2 以降、それまでの Rotate Euler、Align Euler to Vector ノードがそれぞれ、Rotate Rotation、Align Rotation to Vector ノードに改称された。
個人的には余計な混乱を生むだけの改悪だと思うし、理由はよくわからないが、Euler Angle(オイラー角)が一般には用語的にわかりづらく、「Rotation」にしておきましょう、と判断されたのかもしれない。
まとめ
頂点を回転させることですこし複雑な形状ができることがわかりましたが、ここまでジオメトリノードを組む過程で、さまざまなデータの種類があり、ノードをつなぐひしがたや丸などのソケットもいくつかあり、すこし混乱することもあると思いますし、わたしもまだ混乱しています。
そこで、次回では、そのデータタイプとソケットについて紹介しようと思います。
回転ベクトルというものの「やさしい」解説を読んでみましたが、正直いって、火星人のことばを理解しようとするほうがわたしにはまだ楽です。
