
1つの定理を4通りの方法で証明した話
この記事は、日曜数学 Advent Calendar 2022 の14日目の記事です。
昨日はひろまるさんの「ある代数曲面上の有理点を無限個有する有理曲線について」でした。
Twitterには面白い数学系botがたくさんいる。
最近見つけたこのbotも面白い。名前は「初等幾何bot」。
名前の通り、初等幾何の定理を淡々とツイートしているbotである。
結構知らない定理も多いので、気になる定理を見つけたら証明を考えたりもしている。たいてい証明を思いつかないのだが、証明できると嬉しい。
で、先日、1時間くらい考えてようやく証明できた定理がこちら。
平面上に3点A,B,Cがあり,BCの中点をDとし,AB=CEとなるよう線分AD上にEをとると,∠BAD=∠CED(典型構図) https://t.co/hhE8az4RvB pic.twitter.com/IE08OU5a6S
— 初等幾何bot (@Geometry_bot_) December 10, 2022
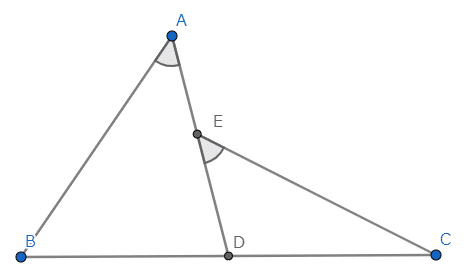
あまり見たことないタイプの主張な気がする。典型構図も珍しい。三角形が二つ、食い違うような姿勢でくっついている。
初等幾何の定理はその多くが、見た目が対称的だったりしてアートっぽさがあったりするが(それは人間がそう見えるように点を配置しているからでもあるが)、この定理はそうなっていない。アンバランスさしかない。
ということで気になって、証明を考えてみた。
このあとすぐその証明を始めるので、自力で考えたい人はここで読むのをやめて欲しい。
では証明を始めよう。
線分CEを延長して、線分ABとの交点をFとする。

すると、メネラウスの定理から以下の式が成立する。

ここで、AB=CE、BD=DCなので、この式は結局、

となり、EF=FAが得られる。

FA=FEなので、△AFEは二等辺三角形である。
よって底角が等しいので、∠FAE=∠FEA
そして対頂角は等しいので、∠FEA=∠DEC
以上から、∠FAE=∠DECが言えた。Q.E.D.
この証明を「数学デー」という場所で紹介したところ、そこに集まった人々から別証明をいくつもいただいた。せっかくなので紹介したい。
1つ目はこちら。

△CEDに合同な三角形を、線分BD上に作るというもの。BD=CDなので、この二辺はピッタリ重ねることができる。
さらに、∠ADB+∠ADC=180°なので、A,D,Fは一直線に並ぶ。したがって図形ABFDは三角形になる。
ここで、辺AB=辺BFなので、△ABFは二等辺三角形である。
よって ∠BAD=∠BFD
合同なので ∠BFD=∠DEC
したがって、∠BAD=∠DECである。Q.E.D.
とんでもなくエレガントな証明だ。図を見れば一発で理解できる。
これを紹介してしまうとこれ以降の証明の面白みがかすんでしまうのだが、一番綺麗だったので最初に紹介した。
2つ目はこんな方法である。これも面白い。

先ほどはBD=DCであることを利用したが、今度はAB=CEに注目して、この二辺をくっつけた。
ここで、∠ADB+∠EDC=180°なので、∠ADB+∠AFB=180°である。
対角の和が180°なので、四角形ADBFは円に内接する。

ここで、FB=CDなので、FB=BDである。
したがって、ひとつの円において、同じ長さの弦(弧)に対する円周角は等しいので、∠FAB=∠BAD
よって、∠BAD=∠DECである。Q.E.D.
これまたエレガントな証明である。
「一直線を成す二角は、移動させると『対角が等しい四角形』を作れる」
このことは、覚えておいて損はなさそうだ。
最後の証明はこちら。

△DECをk倍に拡大し、△DAFとする。
このとき、辺DF=bk, 辺AF=ak となる。
したがって、△ABFにおいて、
AB:AF=BD:DF
が成り立つので線分ADは∠BAFの二等分線である(二等分線の性質の逆)。
よって、∠BAD=∠DAF=∠DECである。Q.E.D.
角の二等分線の性質を知っていれば、図を見るだけで一発で理解できる証明である。これもなかなかエレガントだ。
以上、ひとつの定理を4通りの方法で証明した。
実はこれ以外にも証明を頂いた。まだまだあるかもしれないので、ぜひ考えてみて欲しい。
明日は龍孫江さんの「可換環についてなにか書きます」です。
